Подробности

Категория: Общее

Опубликовано: 28 апреля 2015

Учебная лаборатория является подразделением кафедры «Высшая математика». На протяжении многих десятилетий лаборатория поддерживает учебный процесс. От правильных и своевременных действий сотрудников лаборатории зависит документооборот на кафедре. Коллектив лаборатории готовит материалы к экзаменам и зачетам, оформляет методические стенды кафедры, учебно-методические комплексы дисциплин, обрабатывает экзаменационные ведомости, ведёт статистический учет успеваемости, вводит данные об успеваемости в систему «Электронный университет», работает с электронной библиотекой, вводит данные UOSP. Сотрудники лаборатории поддерживают режим работы специализированных аудиторий и дисплейных классов, функционирование специализированных устройств обучения (ПК, аудио- и видео-инструментария), обеспечивают техническую поддержку научных конференций, симпозиумов, семинаров.

 

В лаборатории кафедры создан библиотечный фонд – учебники, монографии, которые активно используются студентами, а также собран банк авторефератов диссертационных работ по различным направлениям научной деятельности кафедры.

 

В настоящее время в компьютерном классе кафедры имеется возможность использования современных программных продуктов, необходимых для обеспечения надлежащего в современных условиях уровня подготовки специалистов по дисциплинам, преподаваемым на кафедре. Ближайшей задачей является укрепление материальной базы кафедры за счет приобретения лицензионных программных продуктов и компьютеров для выполнения возрастающего объема научно-исследовательских и учебно-методических работ.

 

Почти тридцать лет лабораторией кафедры руководила Татьяна Викторовна Позднякова. Долгие годы в лаборатории работали инженеры Надежда Григорьевна Куделина, Галина Васильевна Гейкина, Алла Викторовна Кузьмичева, Ирина Андреевна Вальденберг, Татьяна Михайловна Минаева, Татьяна Евгеньевна Богомолова, Татьяна Валентиновна Шмидт, Татьяна Владимировна Крапивина.

 

Современная лаборатория кафедры ФН-1- это молодые, грамотные сотрудники. В составе лаборатории инженеры Юлия Аркадьевна Волкова, Ирина Михайловна Кочарыгина, Ольга Викторовна Чернышева, Светлана Валериевна Марфунина.

 

С 2002 года работой лаборатории кафедры «Высшая математика» руководит Секаева Любовь Ивановна. В 1982 году она окончила МГПИ им. В.И.Ленина. Работает в МГТУ им. Е. Э. Баумана более 40 лет (на кафедре «Высшая математика» с 1976 года).

 

В обязанности заведующей лабораторией входит материальная ответственность, связь с центральной бухгалтерией, Учебным управлением, Отделом кадров, оформление документов на работу сотрудников.

Любовь Ивановна награждена Почетной грамотой Министерства образования и науки РФ.

 

Более 30 лет в лаборатории работает ведущий инженер Волкова Юлия Аркадьевна. В 1992 году она окончила  МГТУ им. Н.Э. Баумана. Юлия Аркадьевна ведет делопроизводство кафедры, оформляет трудовые договора сотрудников, организует прохождение курсов повышения квалификации, конкурсов на замещение должностей профессорско-преподавательского состава.

 

 

С 2007 годав лаборатории работает инженер Кочарыгина Ирина Михайловна. Онаимеет  незаконченное высшее образование. Ирина Михайловна работает с системой «Электронный университет», ведет  статистический учет успеваемости студентов, табель учета рабочего времени, оформляет больничные листы преподавателей, готовит раздаточный материал для проведения занятий.

 

Инженер Марфунина Светлана Валериевна работает на кафедре с 2011 года. Она окончила Московский институт права в 2006 году. Вводит данные в электронную библиотеку, ведет учет нагрузки профессорско-преподавательского состава, вводит данные в компьютер (план работы кафедры, годовые отчеты, работа НИЧ).

 

Инженер Чернышева Ольга Викторовна работает на кафедре с 2009 года. В 2013 году она окончила Университет Российской Академии Образования. Ольга Викторовна работает с системой «Электронный университет», ведет учет экзаменационных, зачетных ведомостей и направлений, работает с индивидуальными планами преподавателей.

 

 

 

Работа лаборатории не всегда заметна, но она является неотъемлемым звеном в механизме работы кафедры. Сотрудников лаборатории отличает большой творческий потенциал, трудолюбие, честность, скромность, доброжелательность в отношениях с преподавателями, умение создать деловую атмосферу в работе. Дружным коллективом лаборатории на кафедре организуются праздники, поздравления юбиляров.

 

Подробности

Категория: Общее

Опубликовано: 21 марта 2015

 

Становление научной школы математики

МГТУ им. Н.Э.Баумана

 

От воспитательного дома до высшего технического училища

 

Образование Московского ремесленного учебного заведения (МРУЗа) в 1830 году явилось одним из многочисленных мероприятий по развитию и совершенствованию образования в России, проводимых под непосредственным контролем императора Николая I. В послании министру просвещения от 14 мая 1826 года императором было предписано создать особый Комитет устройства учебных заведений. Перед ним ставились жесткие требования: сравнить все уставы учебных заведений империи, начиная от приходских училищ до университетов; рассмотреть и сравнить курсы обучения, собрав учебные пособия и руководства, ввести единообразие в учебную систему.

 

Перед новым учебным заведением — МРУЗом — были поставлены серьезные задачи: принять на обучение до 300 воспитанников с тем, чтобы сделать из них не только хороших ремесленников, но и искусных мастеров с теоретическими знаниями, служащими для усовершенствования ремесел и фабричных работ.

 

Для проведения учебных занятий был утвержден штат из четырех профессоров, десяти преподавателей по разным предметам, одного механика для управления всеми работами, 18 мастеров по различным ремеслам и одного смотрителя модельного кабинета, кабинета физики и библиотеки. Общее руководство учебными занятиями осуществлял помощник директора — смотрительклассов. Организационно-хозяйственной деятельностью руководил Комитет училища.

 

С момента начала занятий в МРУЗе преподавали алгебру и геометрию, с 1834 года — физику, химию и механику и с 1838 года — практическую механику, прикладную химию и начертательную геометрию.

 

Первым профессором-математиком МРУЗа был выдающийся педагог Платон Николаевич Погорельский (1800-1852). Он окончил физико-математическое отделение Московского Университета, после чего в 1827 году выдержал экзамен на степень магистра физико-математических наук и в том же году получил ее, защитив диссертацию "О способах определять удельный вес тел». П.Н.Погорельский преподавал математику и физику в различных учебных заведениях, среди которых был и МРУЗ. Причиной такого широкого развития преподавательской деятельности П.Н.Погорельского были его замечательные педагогические способности, выражавшиеся в простом, ясном и общедоступном изложении предмета и в редком умении заинтересовать им учеников. П.Н.Погорельский внес большой вклад в развитие учебно-методической работы по практической механике и математике. Им были переведены с французского языка и изданы несколько учебников. К 1863 году учебник П.Н.Погорельского «Курс чистой математики» выдержал восемь изданий.

 

С 1834 по 1838 годы занятия по математике в МРУЗе вел Сократ Акимович Акимов, выпускник Московского университета, магистр чистой математики.

 

В целом к 1838 году сложилась стройная система теоретического и практического обучения с соответствующими учебными планами и программами.

 

Предусматривалось шестилетнее обучение. Учебный план включал в себя теоретическую и практическую подготовку по трем разрядам: подготовительному, состоящему вначале из двух, а затем трех классов; мастерскому, состоящему из трех классов, и рабочему.

 

Теоретическое обучение в подготовительных классах включало в себя изучение арифметики, алгебры, геометрии в приложении к ремеслам. В мастерском классе продолжалось освоение этих предметов подготовительного курса, в основном в форме упражнений.

 

В соответствии с новым Уставом, принятым 30 июля 1844 года, в учебный план уже входили следующие математические дисциплины: арифметика, алгебра (до уравнений высших степеней), геометрия, тригонометрия.

 

12 декабря 1857 года по представлению почетного опекуна МРУЗа князя Трубецкого Высочайшим Повелением в училище организуются высшие классыпо двум направлениям: механическому и химическому, а срок обучения увеличивается до девяти лет (три года — в приготовительном разряде, три года — в мастерском и три года — в высшем классе). Тогда же утверждается, что к преподаванию теоретических дисциплин могут допускаться только лица, имеющие ученое звание не ниже магистра (примерно соответствует современной степени кандидата наук) и в состав воспитанников разрешается принимать детей лиц всех свободных сословий.

 

Таким образом, к 1857 году закончился первый этап развития МРУЗа: он встал в один ряд с высшими техническими учебными заведениями Российской империи как по своему устройству и порядку комплектования, так и по уровню квалификации выпускников.

 

К началу 1860-х годов в МРУЗе сложился коллектив преподавателей — воспитанников Московского университета и МРУЗа, которые внесли весомый вклад в развитие и реализацию теоретического и практического обучения в училище. Среди них следует отметить выпускника Императорского Московского университета Сергея Николаевича Зернова, который, будучи профессором МРУЗа, опубликовал в 1868 году в математическом сборнике работу «Замечание об интегрировании уравнения с частными производными первого порядка по способу Коши».

 

После ухода из МРУЗа С. Н. Зернов преподавал математику в 1-й Московской гимназии, с 1875 по 1877 годы работал директором Муромского Реального Училища. После этого он был переведен в Тульское реальное училище на должность директора.

 

К началу 1860-х годов в МРУЗе сложилась своя система подготовки механиков и технологов, во многом превосходившая аналогичные системы в России и европейских странах. Большую роль в ее развитии в области теоретического образования сыграли выпускники Московского университета, а в области практического образования — выпускники МРУЗа.

 

В 1859 году директором училища был назначен профессор Александр Степанович Ершов (1818-1867),выпускник физико-математического факультета Московского университета, магистр чистой и прикладной математики. Он направил все свои усилия на коренную реорганизацию МРУЗа. По инициативе А. С. Ершова 12 декабря 1860 года почетный опекун МРУЗа Д.А.Ахлестышев направил в Опекунский совет записку о необходимости коренного преобразования ремесленного учебного заведения.В ней предлагалось переименовать МРУЗ в Техническую школу Московского воспитательного дома, а выпускникам высшего разряда присваивать звание инженера-механика или технолога-химика в зависимости от выбранного ими отделения. Эта записка имела длительное обсуждение, и в результате была предложена реформа более глубокая, чем просто повышение статуса учебного заведения, что в итоге привело бы к разрушению сложившейся системы обучения. Руководство МРУЗа с этим не согласилось и реформы не произошло.

 

В 1866 году А.С.Ершов возобновил работу по преобразованию МРУЗа в высшее техническое училище (впоследствии Императорское Московское техническое училище). В этом же году Опекунский совет рассмотрел новый штат и Устав, в котором, в частности, было записано: «ИМТУ, состоящее в ведомстве Императрицы Марии Федоровны, есть высшее специальное учебное заведение, имеющее основной целью образовывать механиков-строителей, инженеров-механиков и инженеров-технологов».

 

В 1867 году комиссию по дальнейшей подготовке устава после смерти А.С.Ершова возглавил назначенный директором МРУЗа В.К.Делла-Вос, и 1 июня 1868 года новый уставвысшего технического учебного заведения был утвержден. Московское ремесленное учебное заведение было преобразовано в Императорское Московское техническое училище — ИМТУ. В соответствии с уставом оно готовило инженеров-механиков, механиков-строителей (в современном понимании инженеров-машиностроителей) и инженеров-технологов на двух факультетах — механическом и химическом.

 

Императорское московское техническое училище

 

После преобразования МРУЗа в ИМТУ количество заявок на обучение в два с половиной раза превысило число вакансий. Однако руководство училища не могло принять всех желающих обучаться по двум причинам: специфичный учебный план ИМТУ не позволял прошедшим гимназический курс без предварительной подготовки поступить в общие классы, и в то же время училищу остро не хватало помещений.

 

Для устранения указанного несоответствия ректор ИМТУ В.К.Делла-Вос предложил свои услуги Министерству народного просвещения по разработке новых учебных планов реальных училищ и гимназий. Итогом активной работы с участием профессоров и преподавателей ИМТУ в 1874 году стало утверждение нового устава реальных школ, в соответствии с которым в них вводился седьмой год обучения, предназначенный преимущественно для подготовки учащихся к поступлению в высшие специальные учебные заведения. Кроме того, профессора ИМТУ читали лекции в реальных училищах, пробуждавшие у молодежи интерес к технике. Прием в Московское техническое училище показал результаты этой многолетней работы. Если в 1868 году, когда МРУЗ было преобразовано в высшее политехническое учебное заведение, в нем обучалось 300 студентов, то в 1894 году их число увеличилось до 596 человек (из них 22 иностранца), а к 1902 году составило уже более 1000 человек.

 

Сразу же после утверждения Устава руководство ИМТУ организовало работу по созданию и развитию кафедр на базе действовавших в МРУЗе кабинетов. Одной из первых в 1868 году была создана кафедра «Высшая математика», которую возглавил Алексей Васильевич Летников (1837-1888), надворный советник, выдающийся российский математик и педагог. Ему помогали преподаватели математики П.А.Чирков, А.А.Ломовский и В.В.Преображенский.

 

А.В.Летников родился в Москве, окончил здесь гимназию и Межевой институт, был в течение двух лет вольнослушателем Московского университета, а затем три года слушал лекции крупных французских математиков Серре, Шаля, Бертрана, Лиувилля, Пюизе и других в парижской Политехнической школе при Сорбонне. В 1860 году он вернулся в Москву и начал читать курс теории вероятностей в Межевом институте.

 

В первом томе «Математического сборника» (1866) А.В.Летников опубликовал свою первую научную работу по теории дифференциальных уравнений, в том числе уравнения Риккати. В 1867 году ему была присуждена степень доктора Лейпцигского университета по теории дифференциальных уравнений. Международное признание дало ему право без университетского диплома сдать магистерские экзамены, а затем и успешно защитить магистерскую диссертацию на тему «Теория дифференцирования с произвольным указателем».

 

Идеи магистерской диссертации А.В.Летникова «Теория дифференцирования с произвольным указателем» были в дальнейшем развиты им в докторской диссертации «Исследования, относящиеся к теории интегралов вида 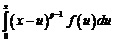», напечатанной в «Математическом сборнике» (т. 7, 1874 г.). При помощи предложенной им теории дифференцирования с дробным показателем ему удалось создать новый метод анализа особенностей решений обыкновенного дифференциального уравнения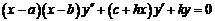 , которое обобщает важные классы дифференциальных уравнений: гипергеометрическое, Бесселя, уравнения многочленов Лежандра и Чебышева. В 1882-1885 гг. в тт. 10-12 «Математического сборника» он опубликовал статьи о модификации этого метода применительно к сферическим функциям.

 

Научные труды А.В.Летникова заслужили всеобщее признание, что было подтверждено избранием его в 1884 году членом-корреспондентом Петербургской академии наук. Академики В.Г.Имшенецкий, В.Я.Буняковский и С.А.Баклунд в своем представлении к избранию писали: «В большей части научных работ проф. Летникова обращает на себя внимание постоянство их направления к одной научной цели, выдержанные в течение многих лет и увенчавшиеся полным успехом. В целом ряде статей своих, помещенных в различных томах сборника Московского Математического общества, он тщательно проследил первое проявление, видоизменения и развитие идеи о так называемом дифференциальном исчислении с произвольным указателем. Прочная научная постановка метода и развитие приложений междупредельного дифференцирования представляет настолько замечательную научную заслугу, что было бы излишним входить в рассмотрение других научных трудов г. Летникова, имеющих, впрочем, несомненные достоинства».

 

Идеи А.В.Летникова в работах этого цикла непосредственно перекликались с идеями магистерской диссертации М.Е.Ващенко-Захарченко «Символическое исчисление и приложение его к интегрированию линейных дифференциальных уравнений» (1862 г., Киев) об упрощении решения дифференциальных и разностных уравнений. Серия работ английского ученого О.Хевисайда по применению операционного исчисления к решению электротехнических задач была начата лишь в 1887 году, причем в этих работах использовались подходы, сходные с идеями М.Е.Ващенко-Захарченко и А.В.Летникова, но без достаточно строгого математического обоснования.

 

Научная работа А.В.Летникова была тесно связана с его педагогической деятельностью, что сыграло важную роль в математической подготовке инженеров в училище. Сложился характерный для А.В.Летникова стиль чтения лекций: простота, ясность при одновременной оригинальности математических доказательств.

 

Программа курса математики для различных отделений училища в то время включала аналитическую геометрию, анализ, сферическую геометрию, начала дифференциальной геометрии и высшей алгебры. Из специальных курсов выделялся прочитанный А.В.Летниковым курс вариационного исчисления, позднее вышедший отдельным изданием. А.В.Летников был автором руководств по общим разделам анализа — дифференциальному и интегральному исчислению и их приложениям, дифференциальным уравнениям.

 

А.В.Летников помимо кафедры высшей математики возглавлял в училище и комиссию по разработке общей системы теоретической и практической подготовки инженеров, получившей всемирную известность как «русский метод обучения ремеслам», преподавал математику в Межевом институте, а с 1883 года был директором Московского коммерческого училища. Будучи одним из инициаторов создания и учредителей Московского математического общества, ученый сделал на его заседаниях 15 докладов, материалы которых печатались в выпускаемом этим обществом «Математическом сборнике». В частности, в т. 3 этого сборника (1868) он впервые опубликовал на русском языке в своем переводе с немецкого одну из определяющих работ Н.И.Лобачевского «Геометрические основания теории параллельных». В предисловии к этой публикации А.В.Летников по достоинству оценил революционный переворот в геометрии, осуществленный Н.И.Лобачевским, и в дальнейшем в числе немногих русских математиков настойчиво пропагандировал его идеи. По инициативе А.В.Летникова в «Математическом сборнике» был создан специальный раздел по вопросам методики преподавания математики, причем не только высшей, но и элементарной. В этом разделе он напечатал несколько статей методического характера. Этим же вопросам была посвящена его речь "О системах реального образования", произнесенная им в ИМТУ в 1871 году во время ежегодной торжественной церемонии выпуска студентов.

 

Алексей Васильевич Летников ушел из жизни 28 февраля (11 марта) 1888 года. На первом после его кончины заседании Педагогического совета ИМТУ коллеги почтили память выдающегося ученого. Директор училища И.В.Аристов выступил с речью, в которой отметил огромную эрудицию А.В.Летникова, его близкое знакомство с постановкой учебного дела во многих высших учебных заведениях, не только русских, но и иностранных. Профессор Ф.Е.Орлов назвал А.В.Летникова гуманным воспитателем юношества, на которое он производил неотразимое впечатление возвышенным образом мыслей, прямотою и искренностью своего характера, неподкупной честностью и неуклонным исполнением долга.

 

На формирование научной школы математики в училище оказала большое влияние деятельность выдающегося русского математика и механика академика Пафнутия Львовича Чебышева (1821-1894), у которого с преподавателями училища были давние дружеские отношения, несмотря на то, что научная жизнь ученого была связана главным образом с Санкт-Петербургом. В отчете училища за 1871 год впервые была опубликована его работа "О центробежном уравнителе", которая явилась первым фундаментальным исследованием по теории регуляторов. В статье «О зубчатых колесах», напечатанной в 1872 году в сборнике «Отчет и речи, произнесенные в торжественном собрании Императорского Московского технического училища 22 сентября 1872 года», он изложил аналитический метод расчета зубчатого зацепления.

 

В последующие годы П.Л.Чебышев, будучи почетным членом Педагогического совета ИМТУ, регулярно посещал училище, чтобы руководить изготовлением и испытаниями в механической лаборатории спроектированных им регуляторов и других механизмов и устройств. Стремление усовершенствовать шарнирный механизм, называемый параллелограммом Уатта, натолкнуло его на постановку проблемы наилучшего приближения функций, заложившей основы глубокой математической теории, значение которой оказалось существенно шире первоначальной прикладной задачи. Ему принадлежит полушутливое высказывание о взаимосвязи теории и практики: «Математика пережила ранее два периода. В первом задачи ставились богами (делосская задача об удвоении куба), во втором — полубогами (Б.Паскаль, П.Ферма). Мы вошли теперь в третий период — задачи ставит нужда (практика), причем чем задача труднее, тем плодотворнее должны быть математические методы ее решения и тем шире область их последующего применения».

 

В те первые десятилетия в штате кафедры «Высшая математика» было всего несколько человек: профессор – заведующий кафедрой и два-три преподавателя.

 

В течение нескольких лет на кафедре работал Владимир Васильевич Преображенский (1846—1905). Он в 1868 году окончил физико-математический факультет Московского университета и был оставлен для приготовления к профессорскому званию. В 1874 году В.В.Преображенский защитил в Московском университете магистерскую диссертацию «Об интегрировании уравнений с частными производными второго порядка», а в 1879 году — докторскую «О логарифмическом потенциале».

 

Кроме ИМТУ В.В.Преображенский преподавал на Лубянских женских курсах, в шестой московской гимназии; был доцентом и потом профессором Новороссийского университета, профессором Казанского университета и приват-доцентом Санкт-Петербургского университета.

 

В.В.Преображенский – автор ряда научных работ, среди которых выделяются: «Частный случай движения жидкой площади», «Об устойчивости равновесия твердого тела под действием центральной силы», «Интегрирование уравнений с частными производными второго порядка», «Об интегрировании Лапласова уравнения с помощью кватернионов», «О начале наименьшего действия», «Элементарный вывод формулы маятника», «Дифференциальный воздушный калориметр», «Геометрическая теория преломления света», «Сложение произведений без помощи умножения» «Применение начала живых сил к действию машин».

 

В 1871 году безвременно ушел из жизни молодой преподаватель Александр Александрович Ломовский, выпускник физико-математического факультета Московского университета. В 1868 году А.А.Ломовский выдержал экзамен на степень магистра чистой математики и приступил к работе над магистерской диссертацией по теории функций мнимого переменного. С 1868 по 1871 годы А.А.Ломовский вел занятия в 3 подготовительном и 1 общем классах ИМТУ.

 

Покинули кафедру преподаватели Владимир Васильевич Преображенский и Павел Алексеевич Чирков. Им на смену пришел магистр прикладной механики надворный советник Н.Е.Жуковский.

 

Выдающийся русский ученый-механик Николай Егорович Жуковский (1847-1921), который своими математическими исследованиями оказал влияние на развитие научной школы математики, в том числе в области качественной теории дифференциальных уравнений, окончил физико-математический факультет Московского университета в 1868 году по специальности «Прикладная математика».

 

После окончания университета Н.Е.Жуковский работал преподавателем во Второй женской гимназии, а вянваре 1872 года он был утвержден преподавателем математики в Императорском Московском техническом училище (ИМТУ), с которым навсегда связал свою жизнь. В 1879 году Н.Е. Жуковский был утвержден в должности сверхштатного профессора кафедры аналитической (теоретической) механики, и совмещал эту должность с должностью преподавателя математики до 1887 года, когда он был утвержден штатным профессором кафедры теоретической механики, уже будучи доктором прикладной математики (ученую степень доктора Н.Е.Жуковский получил в 1882 году за работу «О прочности движения»).

 

В Московском университете Н.Е. Жуковский был утвержден приват-доцентом в 1885 году, в следующем — экстраординарным профессором, а с 1887 года заведующим кафедрой механики, где также работал непрерывно до конца своей жизни.

 

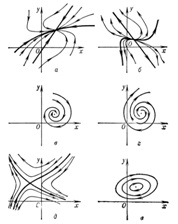
В своей магистерской диссертации «Кинематика жидкого тела», опубликованной в т. 8 «Математического сборника» (1876), при рассмотрении некоторых случаев плоскопараллельного движения несжимаемой жидкости он ввел классификацию особых точек дифференциальных уравнений первого порядка, которая содержала все четыре основных вида особых точек («узел», «седло», «фокус», «центр»), систематизированных затем в работах одного из признанных создателей качественной теории дифференциальных уравнений французского математика А.Пуанкаре.

 

Н.Е.Жуковский также исследовал поведение интегральных кривых в окрестности особой точки каждого вида. Однако это направление исследований, являвшееся лишь ответвлением его работ по механике, в дальнейшем не получило продолжения. Но авторитет Н.Е.Жуковского в развитии качественной теории дифференциальных уравнений был настолько высок, что в 1892 году он выступил в Московском университете оппонентом на защите А.М.Ляпуновым докторской диссертации «Общая задача об устойчивости движения», в значительной мере определившей основные идеи и методы последующих работ в этой области.

 

Глубокая и взаимно обогащающая связь научных исследований по математике и механике, ярко проявившаяся в работах Н.Е.Жуковского, была характерна для научных школ этих направлений. Например, решение им задачи определения гидродинамических сил, в том числе подъемной силы при обтекании крыла воздушным потоком, в значительной мере повлияло на развитие разделов теории функций комплексного переменного, связанных с методами конформных отображений. Признанием авторитета Н.Е.Жуковского в области математики явилось избрание его в 1905 году президентом Московского математического общества, постоянным членом которого он состоял с 1876 года.

 

В 1894 году Н.Е.Жуковский был избран членом-корреспондентом Российской Академии наук. В 1900 году его кандидатуру выдвинули в действительные члены Академии наук. Но Николай Егорович отказался принять это почетное предложение, так как положение академика обязывало его переехать в Петербург. Он не мог решиться покинуть Москву, оставить преподавание в ИМТУ и Московском университете, налаженные им кабинеты и лаборатории, а также многочисленных своих учеников.

 

Среди учеников Н.Е.Жуковского следует отметить преподававшего в ИМТУ в 1896-1906 годах математику и аналитическую механику одного из основоположников современной гидроаэродинамики Сергея Алексеевича Чаплыгина (1869-1942). Он разработал приближенный метод интегрирования обыкновенных дифференциальных уравнений первого порядка и их систем, вошедший затем в математическую литературу под названием метода Чаплыгина.

 

В 1884 году был избран в доценты кафедры «Высшая математика» магистр чистой математики Московского университета коллежский советник Николай Александрович Шапошников (1851-1920). Ему было поручено преподавание математики в первом общем классе. Н.А.Шапошников читал лекции по аналитической геометрии на плоскости, высшей алгебре, дифференциальному исчислению. Во втором и третьем общих классах лекции по-прежнему читал А.В.Летников (аналитическая геометрия в пространстве, высший анализ, дифференциальное исчисление функций нескольких переменных, интегральное исчисление). В 1888 году Н.А.Шапошникову было поручено чтение лекций во втором и третьем классах после смерти А.В.Летникова. Н.А.Шапошников и возглавил кафедру «Высшая математика», при этом некоторое время он оставался ее единственным сотрудником. В 1890 году Н.А.Шапошников, уже статский советник, был утвержден в должности профессора, а кафедра пополнилась известными российскими математиками конца XIXвека К.А.Андреевым, Е.А.Болотовым, Д.Н.Горячевым, Л.К.Лахтиным, А.А.Волковым.

 

Николай Александрович Шапошников был выдающимся педагогом. Курсы его лекций были для того времени образцовыми, а составленные им учебные пособия долгое время являлись основными почти во всех технических вузах России. Он, как и А.В.Летников, интересовался вопросами методики преподавания элементарной математики и ее  связью с методикой преподавания высшей математики. Н.А.Шапошников был автором ряда учебников по элементарной и высшей математике («Курс арифметики», «Основания общей арифметики и алгебры», «Основания теории детерминантов», «Курс тригонометрии», «Алгебра», «Основной курс математического анализа»), а составленный им в соавторстве с  Н.К.Вальцовым «Методический сборник алгебраических задач» выдержал с 1887 по 1917 годы 24 издания, а после 1917 года — еще 28 изданий.

 

Одним из лучших исследований Н.А.Шапошникова является оригинальная работа «Интегрирование дифференциальных уравнений с полными дифференциалами и частными производными первого порядка». В этой работе Н.А.Шапошников дал краткий и общий прием для вывода формул, названных им «дифференцио-дифференциальными соотношениями», а также применения этих соотношений к решению основного вопроса теории интегрирования — вопроса о разыскании простейших уравнений, к которым сводится интегрируемое уравнение.

 

В статье «Дифференцио-дифференциальные соотношения и их применение в общем методе интегрирования уравнений с частными производными» Н.А.Шапошников показывает, что разработанные им приемы и методы дают с несравненной простотой и общностью те результаты, которые другими путями достигаются сложными и искусственными вычислениями. Эти работы по существу развили новый принцип в математике, дав общий метод интегрирования определенного вида уравнений.

 

Под руководством Н.А.Шапошникова преподавателями кафедры были подготовлены и изданы важнейшие курсы: «Курс аналитической геометрии» К.А.Андреева, «Анализ и аналитическая геометрия» Д.Н.Горячева, «Математический анализ» Е.А.Болотова, курсы по аналитической геометрии Л.К.Лахтина. Что касается курса математического анализа, то учебник Н.А.Шапошникова (достаточно полный, но сухой по изложению и несколько трудный для понимания) быстро был вытеснен двухтомным литографированным курсом Е.А.Болотова, который отличался оригинальностью изложения и содержал важные для практических приложений сведения — например, вывод весьма удобной формулы квадратур Понселе, которого нет ни в одном из курсов анализа других авторов.

 

В годы революции Н.А.Шапошников, уже вышедший в отставку, оказался в Геленджике, где преподавал в женской гимназии. В сентябре 1918 он был приглашен Б.Л.Розингом в Екатеринодар (ныне Краснодар), где стал ректором только что открывшегося Северо-Кавказского политехнического института и его профессором математики. Н.А.Шапошников отстаивал сохранение СКПИ, когда над ним нависла угроза закрытия со стороны белоказачьих властей, в частности, в своей статье «Два законопроекта», опубликованной газетой «Кубанский край» (15 ноября 1918 года).

 

В 1896 году начал свою работу на кафедре Евгений Александрович Болотов (1870-1922), известный математик и механик, выпускник Казанского университета. Его научные исследования относятся главным образом к аналитической механике. В 1907 году Е.А.Болотов был утвержден в степени магистра прикладной математики за работу на тему «О движении материальной плоской фигуры, стесненной связями с трением». В своем отзыве на эту работу Н.Е.Жуковский отметил, что главная заслуга Е.А.Болотова в этой работе – его геометрический анализ.

 

Самой значительной работой Е.А.Болотова по аналитической механике является его исследование наиболее общего вариационного принципа механики – принципа наименьшего принуждения Гаусса. Е.А.Болотову принадлежит обобщение принципа наименьшего принуждения, которое легло в основу дальнейших исследований этого принципа учеными казанской школы механики. Представляют также интерес работы Е.А.Болотова по гидромеханике и учебные руководства по курсам математического анализа и аналитической геометрии, которые ученый много лет читал в Московском техническом училище. В училище он читал курс аналитической геометрии и одновременно вел упражнения по теоретической и аналитической механике, лекции по которой читал Н.Е.Жуковский.

 

В лекциях по аналитической геометрии Е.А.Болотов излагал аналитическую геометрию на плоскости и в пространстве, а также сферическую тригонометрию, увязывая многие разделы этого курса с отдельными вопросами теоретической механики и астрономии.

 

Е.А.Болотов уделял большое внимание подготовке своих лекций. Он обрабатывал их настолько детально и тщательно, что при издании их почти не требовалось редактировать.

 

С 1914 по 1921 год Е.А.Болотов заведовал кафедрой теоретической механики Казанского университета, а в 1921-1922 годах – кафедрой теоретической механики МВТУ.

 

Известный российский математик Константин Алексеевич Андреев(1848— 1921) в 1867 году поступил на математическое отделение физико-математического факультета Московского университета. Первый его научный труд, написанный в 1870 году на тему, предложенную факультетом — «О таблицах смертности», был удостоен награждения золотой медалью. После окончания университета в 1871 году он был оставлен при нем стипендиатом для приготовления к профессорскому званию.

 

В 1875 году К.А.Андреев защитил магистерскую диссертацию: «О геометрическом образовании плоских кривых», в 1879 году - докторскую: «О геометрических соответствиях в применении к вопросу о построении кривых линий». В 1884 году избран Академией Наук в члены-корреспонденты. Был председателем образовавшегося в 1879 году при Харьковском университете Математического общества и редактором его трудов.

 

Основные труды К.А.Андреева относятся к проективной геометрии и математическому анализу. Он является автором известного учебника «Основной курс аналитической геометрии» и сборника упражнений по аналитической геометрии, а также историко-биографических очерков по геометрии.

 

В конце 19 – начале 20 века К.А.Андреев, действительный статский советник, преподавал в ИМТУ, Московском Университете и других учебных заведениях. В ИМТУ он вел занятия по аналитической геометрии на 1 курсе механического отделения. Был председателем Педагогического совета ИМТУ. С 1898 года — заслуженный профессор Московского университета и, одновременно, директор Александровского Коммерческого Училища. С 1905 года по 1911 год был деканом физико-математического факультета Московского университета.

 

В конце 19 – начале 20 века на кафедре работал статский советник Леонид Кузьмич Лахтин (1863-1927), российский математик, специалист в области решения алгебраических уравнений высших степеней, а также в области математической статистики. Он вел занятия на 1 курсе химического отделения. Л.К.Лахтин был заслуженным профессором Московского университета, ректором Московского университета (1904—1905), деканом Физико-математического факультета Московского университета (1912—1918). Его магистерская диссертация «Алгебраические уравнения, разрешимые в гипергеометрических функциях» посвящена исследованию уравнений 3-й, 4-й, 5-й и одного вида 6-й степени. В 1897 году он защитил докторскую диссертацию «Дифференциальные резольвенты алгебраических уравнений высших родов».  

 

В 1924 году Л.К.Лахтин опубликовал большой учебник по теории вероятностей.

 

Доктор прикладной математики, профессор Дмитрий Никанорович Горячев (1867 - 1949) вел с 1898 по 1909 годы практические занятия по математике и аналитической механике на механическом отделении ИМТУ. Д.Н.Горячев окончил в 1889 году физико-математический факультет Московского университета. Защитил в 1899 году магистерскую диссертацию «О некоторых случаях движения прямолинейных параллельных вихрей», а в 1912 году - докторскую диссертацию «Некоторые общие интегралы в задаче о движении твердого тела».

 

Основные направления его научной работы: общая механика, динамика твердого тела с одной неподвижной точкой, гидродинамика. 

 

Д.Н.Горячев - автор более 40 научных работ, среди которых «Новое частное решение задачи о движении тяжелого твердого тела», «О движении тяжелого твердого тела вокруг неподвижной точки в случае А=В=4С», «Некоторые случаи симметричного относительно оси движения жидкости».

---

 

Училище на стыке эпох

 

В конце XIX века в стране происходили многочисленные студенческие волнения, не обошедшие стороной и ИМТУ. Однако в его стенах они не были столь бурными, как, например, в Императорском Московском университете. В 1895 году был утвержден новый устав ИМТУ, согласно которому срок обучения снижался до пяти лет. Существенно ограничивались права Учебного комитета — в его ведении оставались только приемные и переводные экзамены, рассмотрение семестровых отчетов по учебным делам и утверждение учебной и научной литературы, подготовленной сотрудниками училища. В соответствии с уставом в штате ИМТУ предусматривалось только одиннадцать профессоров и шесть адъюнкт-профессоров. Данные ограничения явились частью общей государственной политики, направленной на предотвращение возможных социальных потрясений.

 

13 января 1905 года в связи с происходящими революционными событиями в ИМТУ, как и в других вузах, занятия прекратились и не проводились (с небольшим перерывом) более года. Это единственный год, когда вуз не выпустил ни одного специалиста. Тем не менее, в 1905 году прием на первый курс состоялся, и на 220 вакантных мест было подано 705 заявлений. Более того, воспользовавшись вынужденным перерывом, профессорско-преподавательская коллегия подготовила и реализовала давно назревавшую коренную перестройку системы обученияв училище, на разработку которой раньше не хватало времени.

 

Была введена новая, предметная система обучения, предоставлявшая возможность каждому студенту самостоятельно определять продолжительность и содержание своего обучения в рамках 35 вновь введенных специализаций. Для этих специализаций было подготовлено 25 новых учебных курсов и коренным образом пересмотрено содержание всех существовавших. В целом были выделены три группы дисциплин: основные науки и технические дисциплины, специальные предметы и общеобразовательные курсы из области социально-экономических и исторических наук.

 

Новая система обучения была вызвана к жизни существенным расширением спроса на инженеров различных специальностей, с одной стороны, и объявлением широких гражданских свобод, с другой. В числе последних декларировалась и автономия высших учебных заведений, в результате которой ИМТУ смогло самостоятельно изменить весь учебный процесс и впервые в своей истории выбрать руководителя вуза.

 

Первым выборным директором (ректором) училища стал профессор Александр Павлович Гавриленко, которого впоследствии преподавательская коллегия избирала на эту должность еще четыре раза.

 

Начавшаяся мировая война существенно изменила жизнь училища. Наряду с организацией производства вооружения и химических веществ, работой профессоров и преподавателей по заказам оборонных предприятий, сдачей части помещений под госпитали, училищу пришлось решать неожиданно сложную задачу, связанную с призывом студентов в армию.

 

Февральскую революцию коллектив училища принял с энтузиазмом. Эта революция многими воспринималась как обретение долгожданной свободы и начало эпохи процветания. Учебный комитет активно работал по завершению преобразования МВТУ в школу политехнического типа. Решением Учебного комитета от 6 марта 1917 года училище получило новое название — Московское высшее техническое училище (МВТУ).

 

В июле 1917 года были разработаны «Главные основания управления МВТУ». Многие профессора и преподаватели участвовали в работе общественных организаций и органов местного самоуправления, не прекращая своей научно-инженерной деятельности. Однако к осени 1917 года отношение научно-инженерной интеллигенции, равно как и большинства населения, к Временному правительству изменилось не в лучшую сторону. Этому способствовал и тот факт, что весь летний (1917 г.) набор студентов был призван в армию.

 

После Октябрьской революции 1917 года ситуация в стране и вузах в большинстве случаев существенно ухудшилась. В немалой степени этому способствовало тяжелое социальное и экономическое положение, вызванное Первой мировой и гражданской войнами.

 

Большая часть интеллигенции отрицательно восприняли Октябрьскую революцию. Например, в декабре 1917 года учебный комитет училища принял следующее решение: "Принципиально не допуская никакого вмешательства в жизнь автономной школы, выразить решительный протест против на­значения комиссара, если бы такое назначение состоялось".

 

В первые годы советской власти было принято немало необдуманных скоропалительных решений. Например, к августу 1918 года относится принятие Декрета о правилах приема в вузы РСФСР, в соответствии с которым любое лицо, достигшее 16-летнего возраста, могло поступить в вуз без аттестата и экзаменов. В октябре того же года был принят Декрет о некоторых изменениях в составе и устройстве государственных вузов РСФСР. Этот Декрет отменил все ученые степени и ученые звания, кроме звания профессора. При этом профессором именовали всякое лицо, которое проводило самостоятельную преподавательскую работу. Таким образом, количество профессоров в МВТУ существенно увеличилось. Вскоре последовал декрет об отмене всяческих дипломов и выпускники МВТУ, закончившие училище в то время, получали только справку об обучении. Выпуск специалистов стал нерегулярным: защиты дипломов назначались по мере их готовности, независимо от ранее принятых сроков, группами по 5-7 человек. Всего за годы гражданской войны МВТУ выпустило только 128 инженеров.

 

Однако что уже в первые годы советской власти правительство помогло МВТУ справиться с некоторыми проблемами, которые в течение десятилетий не решались в ИМТУ. В частности, в Императорском училище был неоправданно малым штат профессорско-преподавательского состава. Например, по данным на 1912 год, в ИМТУ на одного профессора приходилось — 157 студентов, на одного преподавателя – 38 студентов. Уже в начале 1918 года штатный профессорско-преподавательский состав увеличился в несколько раз. В частности, штат кафедры математики вырос почти до двадцати человек.

 

Кроме того, в апреле 1918 года только что образованный Народный комиссариат просвещения РСФСР принял решение об открытии в ИМТУ двух новых факультетов: инженерно-строительного и электротехнического, а также об открытии инженерно-химического отделения на химическом факультете.

 

С началом гражданской войны существенно уменьшился контингент студентов в училище. Однако почти все преподаватели продолжали работать в эти тяжелейшие голодные и холодные годы в МВТУ. В эти годы относительного затишья в учебном процессе профессора и преподаватели проводили большую организационную и методическую работу по становлению новых инженерно-строительного и электротехнического факультетов.

 

После 1917 года кафедра «Высшая математика» МВТУ играла заметную роль в организации и совершенствовании математического образования в вузах страны. В 1920-х годах при унификации в стране учебных планов подготовки инженеров-механиков по курсу высшей математики за основу был принят учебный план механического факультета МВТУ, представленный и обоснованный деканом этого факультета И.И.Куколевским. В период введения в учебный процесс всевозможных неопробированных новаций научно-педагогическая общественность училища настояла на сохранении лекционной формы обучения, в том числе по математике и другим общенаучным дисциплинам. Представители кафедры активно участвовали в многочисленных дискуссиях по проблемам преподавания математики в вузах и последовательно отстаивали свои позиции. Научно-методические работы преподавателей кафедры регулярно публиковались в сборниках трудов, издававшихся в МВТУ.

 

В эти трудные годы на кафедре «Высшая математика» работали многие выдающиеся советские ученые, в последствие избранные в академию наук СССР. Заведовал кафедрой профессор Алексей Петрович Поляков (1878-1949), выпускник Московского и Гёттингенского Университетов. В 1909 году А.П.Поляков избран преподавателем математики ИМТУ. Кроме того, с 1910 по 1923 годы он работал в должности преподавателя, а затем профессора Московского Института Путей Сообщения по кафедре высшей математики. Автор работ «К теории движения поезда», «Интегрирование уравнения поезда», «Приведение гипергеометрической функции к эллиптическим и гиперэллиптическим интегралам», «О выражении производной любого порядка функции от функции». Неоднократный участник международных математических конгрессов. В 1911 году А.П.Поляков утвержден в должности экстраординарного профессора ИМТУ. Он руководил учебно – методической работой на механическом факультете.

 

После ухода из МВТУ в 1928 году А.П.Поляков работал в ряде учебных заведений, среди которых МПЭИ и МАМИ.

 

В 1920-е годы в состав кафедры высшей математики входили профессора Н.А.Глаголев, В.А.Кудрявцев, Я.Н.Шпильрейн, доценты П.А.Безсонов, Я.С.Дубнов, М.А.Лаврентьев, С.Д.Росинский, П.С.Урысон, В.В.Степанов, С.П.Фиников, ассистенты Д.А.Бем, Е.К.Бренев, И.П.Ветчинкин, А.М.Донде, Б.Н.Иванцов, С.Н.Кузьмин, Н.В.Сахаров, И.И.Соколовский, Б.О.Солоноуц, Л.З.Юделевич, Г.К.Брусиловский, Н.В.Андриевский.

 

Нил Александрович Глаголев (1888—1945) — выпускник Московского университета, профессор, автор трудов по дифференциальной и проективной геометрии, номографии и математической статистике. Руководил первым научным семинаром по номографии и Всесоюзным номографическим бюро. Номограммы, разработанные Н.А.Глаголевым, применялись в различных областях техники, а также в военно-морском флоте и артиллерии. При построении номограмм Н.А.Глаголев использовал проективные методы, впервые применил теорию уникурсальных линейных рядов и получил при этом новые типы. Несколько работ Н.А.Глаголева относятся к вопросам аксиоматики геометрии. Н.А.Глаголев - автор учебника для школы "Элементарная геометрия" (2 ч.), который оказал значительное влияние на перестройку преподавания геометрии в школе.

 

Профессор Московского университета и МВТУ Всеволод Александрович Кудрявцев (1885-1953) известен в первую очередь своим кратким курсом высшей математики (в соавторстве с Б.П.Демидовичем). Ему также принадлежит ряд работ по исследованию распределения корней производных трансцендентной функций, а также по исследованию экстремальных свойств гармонических функций.

 

Доцент Россинский Сергей Дмитриевич (1890—1964), кандидат физико – математических наук, работал на кафедре «Высшая математика» с 1920 по 1932 годы. Его научные интересы лежали в области дифференциальной геометрии, теории конгруэнций, линейчатых поверхностей. Кроме того, ряд работ С.Д.Россинского посвящен исследованию научного творчества К.М.Петерсона и Б.К.Млодзеевского.

 

С 1930 по 1964 годы С.Д.Россинский работал на кафедре высшей геометрии и топологии механико-математического факультета МГУ. После защиты в 1943 году докторской диссертации на тему «Изгибание конгруэнций с сохранением некоторых специальных свойств» утвержден в звании профессора.

 

С 1921 по 1929 годы на кафедре работал Михаил Алексеевич Лаврентьев (1900-1980) - советский математик и механик, в будущем академик АН СССР (1946). Ему принадлежат фундаментальные результаты по теории множеств и общей теории функций, теории приближения функций комплексного переменного, теории конформных и квазиконформных отображений, теории дифференциальных уравнений; им создан ряд новых направлений в этих областях. М.А.Лаврентьев положил начало теории нелинейных классов квазиконформных отображений, поставил ряд новых проблем теории пространственных квазиконформных отображений.

 

В механике сплошной среды и прикладной физике М.А.Лаврентьев также создал ряд новых направлений; им получены крупные результаты в теории крыла, в теории длинных волн, теории струй. М.А.Лаврентьев дал (одновременно с зарубежными учёными) гидродинамическую трактовку явления кумуляции. Основная её идея состоит в том, что при столь высоких давлениях, которые возникают при взрывах, можно с достаточной достоверностью рассматривать металл как несжимаемую жидкость, а образование кумулятивной струи — как задачу о взаимодействии струй жидкости. Это идея, подтвержденная экспериментально, стала основой для дальнейшего развития работ в области кумуляции и оказала влияние на исследование физики взрыва и импульсных процессов вообще. Из работ М.А.Лаврентьева по исследованию процессов кумуляции выросли такие прикладные направления, как теория направленного взрыва, сварка взрывом, высокоскоростной удар, создан новый тип взрывного заряда — шнуровой заряд; они привели М.А.Лаврентьева к созданию советской школы по народнохозяйственному использованию взрыва.

 

Доцент Дубнов Яков Семенович (1887 - 1957) преподавал математику на электротехническом факультете МВТУ с 1921 по 1929 годы. Основные его работы относятся к векторному и тензорному анализу.

 

Я. С. Дубнов в 1906 году поступил на математическое отделение физмата Новороссийского (Одесского) университета, где преподавали известные математики В.Ф. Каган и С.О. Шатуновский. В 1910 году Я.С. Дубнов был награжден серебряной медалью за сочинение «Теория простых определенных интегралов, зависящих от параметра». В этом же году он за участие в студенческом движении был исключен из университета, отбыл полтора месяца в тюрьме и был выслан в провинцию под надзор полиции. Только в 1913 году он сдал экстерном государственный экзамен при Новороссийском университете и снова был выслан из Одессы.

 

С 1918 году Я.С. Дубнов состоял консультантом при Отделе реформы школы Наркомпроса и принимал активное участие в работе секции математики естественного отдела. Одновременно его избрали научным сотрудником НИИМ при МГУ. Я. С. Дубнову принадлежит более пятидесяти научных работ в области дифференциальной геометрии. В 1928 году его работа «Дифференциальная геометрия прямолинейных конгруэнций в тензорном изложении» была принята НИИМ в качестве кандидатской диссертации. А в 1936 году Я.С. Дубнову была присуждена степень доктора физико-математических наук без защиты диссертации на основе многочисленных научных исследований.

 

Я. С. Дубнов известен как выдающийся педагог, автор различных пособий для высшей и средней школы, статей, посвященных вопросам преподавания математики в средней школе. Среди его книг отметим «Задачи и упражнения по дифференциальному исчислению», «Основы векторного исчисления», «Введение в аналитическую геометрию» «Ошибки в геометрических доказательствах», «Беседы о преподавании математики», а также работу «Содержание и методы преподавания математического анализа в средней школе».

 

Доцент Степанов Вячеслав Васильевич (1889 - 1950) окончил физико – математический факультет Московского университета в 1912 году. Его учителем был Д.Ф.Егоров. После окончания университета В.В.Степанов был направлен в научную заграничную командировку в Германию, где он посещал лекции Давида Гильберта и Эдмунда Ландау. В 1915 году он начал научную и педагогическую деятельность.

 

В.В.Степанов является одним из основоположников советской школы в области качественной теории дифференциальных уравнений. Он исследовал свойства важного класса функций, названных почти периодическими функциями Степанова. Им изучены условия существования общего и обобщённого дифференциала для функции двух переменных.

 

В 1928 году В.В.Степанов стал профессором Московского университета, в 1935 году — доктором физико-математических наук. В 1944 году В.В.Степанов был избран вице-президентом Московского математического общества, а в 1946 году — членом-корреспондентом Академии наук СССР.

 

Павел Самуилович Урысон (1898-1924) принадлежал к числу талантливейших советских математиков. Несмотря на недолгую жизнь, он сумел прочно войти в историю математики в качестве одного из крупнейших ученых. Основные результаты получены П.С.Урысоном в области топологии, нелинейных дифференциальных уравнений, геометрии. Ещё в аспирантуре Урысон выполнил несколько ярких научных работ. Они были посвящены теории дифференциальных уравненийи нелинейным уравнениямв бесконечномерном пространстве. П.С.Урысон также доказал теорему из области выпуклой геометрии о том, что шар является телом максимального объёма при фиксированной средней ширине. Совместно с П.С.Александровым П.С.Урысон основал советскую топологическую школу. Создал новое направление в топологии — теорию размерности. Доказал так называемые метризационные теоремы о топологических пространствах.

 

Ассистент Брусиловский Григорий Константинович (1883 – 1950) известен своими многочисленными учебными пособиями по различным разделам элементарной и высшей математики, а также рядом статей методического характера, среди которых отметим следующие: «Единая схема вычисления частного интеграла линейного дифференциального уравнения с постоянными коэффициентами и особенной правой частью» и «Интегрирование с помощью гиперболических функций и гудерманиана». Ему принадлежат интересные доказательства теоремы Помпейю и обобщенной теоремы Птолемея.

 

Г.К.Брусиловский также интересовался вопросами приложения математики к технике. Важным результатом в данном направлении явилась его работа «Зависимость индуктированной ЭДС от шага скрещивания в двухпроводной телефонной цепи».

 

Среди преподавателей кафедры того времени были люди необычной и в то же время трагичной судьбы.

 

Алексей Александрович Солонович (1887-1937) - поэт, философ, теоретик мистического анархизма, в 1914 году закончил физико-математический факультет Московского университета. Тогда же против него возникло судебное дело — в связи с выходом его книги «Скитания духа». Это было произведение мистико-символического содержания. Несмотря на попытки духовной цензуры обвинить А.А.Солоновича в оскорблении религии и нравственности, суд вынес ему оправдательный приговор. В течение нескольких лет А.А.Солонович преподавал математику и механику в гимназиях Москвы и МВТУ им. Н.Э.Баумана.

 

В 1925 году А.А.Солонович арестован уже советской властью и осужден на три года за подпольную анархическую деятельность. Досрочно был освобожден, после чего организовал и руководил рядом анархо-мистических кружков. Его лекции в Кропоткинском музее, где он возглавлял секцию анархистов, пользовались большим успехом у слушателей. Вновь арестован в 1930 году. Погиб в лагере.

 

Евгений Константинович Бренев (1883-1938) - анархо-мистик, член Ордена тамплиеров. В 1924 году в Математическом сборнике была опубликована его статья «Аксиомы порядка в системе аксиом геометрии Гильберта».

 

Е.К.Бренев был арестован в 1930 году как ближайший помощник А.А.Солоновича по проведению анархо-мистических идей в МВТУ, член подпольного кружка, руководимого А.А.Солоновичем, участник нелегальных собраний. Приговорен к трем годам тюремного заключения. В 1932 году выслан в Среднюю Азию; расстрелян в 1938 году по приговору Тройки НКВД.

 

Дмитрий Александрович Бем (1880 - 1938) - анархист-мистик. Один из основателей и руководителей анархо-мистического "Ордена Света". С 1926 года участвовал в деятельности Всероссийского общественного комитета по увековечиванию памяти П. А. Кропоткина (ВОК). Заместитель заведующего Музеем П. А. Кропоткина, председатель библиографического кружка по изучению сочинений М. А. Бакунина. В 1930 году арестован по делу ордена, обвинен в участии в контрреволюционной организации, создании и руководстве подпольными кружками, антисоветской пропаганде. Приговорен к пяти годам тюрьмы, но в связи с оказанием помощи следствию приговор изменен на ссылку в Нарымский округ. После того, как туда же был сослан А. А. Солонович, по заданию НКВД вошел в создаваемый им "Всесоюзный альянс анархистов", сообщал о якобы организованных анархо - мистиками террористических группах и кружках в Сибири и Москве. В 1937 году арестован в ссылке по обвинению в участии в контрреволюционной террористической деятельности. По приговору Военной коллегии Верховного Суда СССР расстрелян.

 

Также был арестован и расстрелян Ян Николаевич Шпильрейн (1887 – 1938) известный математик, член-корреспондент АН СССР. В 1907 году Я.Н.Шпильрейн окончил Сорбонну по отделению физико-математических наук, до 1911 года продолжал обучение в Высшей технической школе в Карлсруэ. Работал в университете Штутгарта. Вернулся в Россию в 1918 году, с 1921 года - профессор МВТУ.

 

Основные научные труды Я.Н.Шпильрейна связаны с применением векторного исчисления и других математических методов в электротехнике, теплотехнике, физике. Я.Н.Шпильрейн - автор статей и монографий, среди которых: «Векторное исчисление. Руководство для инженеров и физиков», «Векторное исчисление для инженеров-электриков и физиков», «Современные математические методы в применении к вопросам электротехники и теплотехники».

 

Я.Н.Шпильрейн был арестован 10 сентября 1937 года по обвинению в участии в «Демократической партии» и приговорен ВК ВС СССР к расстрелу. Расстрелян 21 января 1938 года.

 

Павел Александрович Безсонов, кандидат физико-математических наук, оставил о себе память не только как одаренный математик, но и как прототип литературного персонажа. Он окончил физико-математический факультет Казанского университета в 1916 году. С 1918 года преподавал высшую математику в Казанском Политехническом институте, а с 1920 года в МВТУ. Был членом Московского математического общества.

 

Основными направлениями научной работы П.А.Безсонова были теория функций комплексного переменного и мероморфные функции. В середине 1920 – х годов П.А.Безсонов несколько раз выезжал в научные командировки во Францию, где вел исследования под руководством Ж. Адамара. Ряд статей П.А.Безсонова были опубликованы во французских научных журналах.

 

Длительная переписка Павла Александровича Безсонова и художницы Лидии Андреевны Никаноровой, с которой он познакомился на гимназическом балу, легла в основу одного из лучших романов Вениамина Каверина «Перед зеркалом». В романе они выведены под именами Лизы Тураевой и Константина Карновского.

 

После ухода из МВТУ П.А.Безсонов заведовал кафедрами высшей математики ряда московских институтов.

 

В 1928 году кафедру возглавил Сергей Павлович Фиников (1883-1964), преподававший в ИМТУ с 1913 года. С.П.Фиников - известный специалист в области дифференциальной геометрии. Первые его работы посвящены поиску главных оснований для заданного линейного элемента поверхности. Им исследовано изгибание поверхностей на кинематическом основании. Он был одним из первых геометров, перешедших в своих исследованиях на метод внешних дифференциальных форм. С.П. Фиников сыграл большую роль в распространении идей и методов Картана. В 1948 году вышла его монография «Метод внешних форм Картана», в которой наряду с изложением теории Картана, а также работ Рикье и Томаса, изложены методы определения характеристических многообразий и особых решений систем дифференциальных уравнений.

 

В 1929-1930 гг. кафедрой «Высшая математика» заведовал Александр Яковлевич Хинчин (1894-1959), один из создателей советской школы теории вероятностей, избранный в 1939 году членом-корреспондентом АН СССР. Он перенес методы метрической теории функций в теорию чисел и теорию вероятностей, открыл закон повторного логарифма, заложил основы теории случайных процессов, разработал методы теории массового обслуживания, использовал методы теории вероятностей в качестве математического аппарата статистической физики. А.Я.Хинчин является автором ряда учебников и учебных пособий по математике, выдержавших по три-четыре издания, а "Элементарное введение в теорию вероятностей", написанное им в соавторстве с Б.В.Гнеденко, издавалось 9 раз.

 

В 1930 году произошла самая масштабная за всю историю нашего университета реформа. Московское высшее техническое училище было разделено на пять самостоятельных узкопрофильных вузов. В историческом здании Слободского дворца остался правопреемник МВТУ — Высшее механико-машиностроительное училище, организованное на базе механического факультета и переданное в ведение Наркомата тяжелой промышленности СССР. В июле 1930 года Высшее механико-машиностроительное училище было переименовано в Московский механико-машиностроительный институт (МММИ), которому в декабре того же года было присвоено имя Н.Э. Баумана.

 

Московский механико-машиностроительный институт

 

В 1931 году кафедру «Высшая математика» МММИ возглавил Александр Осипович Гельфонд (1906-1968) — специалист в области теории чисел, теории функций комплексного переменного и конечно-разностных методов. Ему удалось установить глубокие связи между аналитическими свойствами функций комплексного переменного и теорией чисел и создать аналитические методы доказательства трансцендентности чисел. В работах 1929 и 1934 годов им была решена седьмая проблема Гильберта о трансцендентности чисел специального вида, а затем доказан ряд теорем о взаимной трансцендентности чисел. В теории функций ему принадлежат работы по интерполированию целых функций и связи между ростом целых функций и арифметическими свойствами их значений. В 1939 году А.О. Гельфонд был избран членом-корреспондентом АН СССР.

 

В начале 1930-х годов кафедру пополнили несколько преподавателей других вузов. Среди них  Иван Георгиевич Петровский (1901 — 1973) выдающийся математик, академик (с 1946 года) АН СССР. И.Г.Петровский заложил основы общей теории систем дифференциальных уравнений с частными производными; выделил и изучил классы эллиптических, гиперболических и параболических систем; установил аналитичность решений эллиптических систем, изучил задачу Коши для гиперболических и параболических систем, исследовал зависимость решений задачи Коши от начальных данных, установив условия существования лакун и диффузии волн.

 

Работы И.Г.Петровского по теории вероятностей оказали большое влияние на развитие теории случайных процессов. Он изучал вопрос о расположении овалов алгебраической кривой на проективной плоскости. Созданный им метод позволил получить глубокие результаты по топологии алгебраических многообразий любой размерности.

 

В недолгий период работы на кафедре высшей математики МВТУ И.Г.Петровский активно выступал на заседаниях кафедры по методическим и программным вопросам.

 

Доцент Жегалкина-Слудская Мария Ивановна (1882-1968), сестра известного математика Ивана Ивановича Жегалкина, работала на кафедре в 1930-е годы. Ей принадлежит ряд работ по теории приближённых вычислений и методике преподавания высшей математики. Кроме того, М.И.Жегалкина-Слудская известна рядом учебников и задачников по математическому анализу, написанных в соавторстве с И.И.Жегалкиным.

 

В 1933 году кафедра «Высшая математика» вошла в состав общетехнического факультета, организация которого имела цель упорядочить общенаучную и общетехническую подготовку студентов, наладить контакт между кафедрами по согласованию программ читаемых дисциплин. Однако в 1938 году общетехнический факультет был упразднен.

 

В 1930-х годах в институте проводилась большая научно-методическая работа по улучшению проведения основных форм учебных занятий: лекций, семинаров и лабораторных работ. В результате предварительной проработки и всестороннего обсуждения в 1934 году были сделаны следующие рекомендации к проведению лекций: наличие тщательно разработанного плана каждой лекции и предварительное ознакомление с ним студентов (в виде раздаточного материала, вывешивания в аудитории или записи на классной доске). Методически правильное построение и изложение лекции, ясность и наглядность изложения, правильное использование наглядных пособий, четкое выделение основных моментов лекций. Периодический пересмотр содержания лекций и своевременное введение свежих материалов, наличие резюме лекции. Также необходимо было выделить время для ответа на вопросы студентов. В этот период все кафедры МММИ работали над повышением качества лекций. На кафедре «Высшая математика» была поставлена задача сочетать простоту и ясность изложения с достаточной математической строгостью и содержательностью. Методика изложения большинства разделов подвергалась тщательному обсуждению для выявления наиболее целесообразных форм подачи материала.

 

В 1934 году в институте обсуждался вопрос о рациональном проведении всех форм учебных занятий. Было принято, в частности, решение избегать дублирования материалов семинаров и лекций. Например, на кафедре «Сопротивление материалов» каждый лектор делал краткую запись изложенного на лекции материала и передавал ее педагогам, проводившим семинарские занятия. С этой же целью молодые преподаватели кафедры «Высшая математика», проводившие семинары, посещали лекции.

 

Традиционная связь математических исследований на кафедре с работами по механике и их определенная прикладная направленность прослеживаются и на последующих этапах развития научной школы математики нашего университета. В 1932-1936 гг. кафедрой заведовал доктор технических наук, профессор Дмитрий Юрьевич Панов (1904–1975). Кроме того, Д.Ю.Панов в течение 9 лет был деканом факультета точной механики и оптики, а также работал по совместительству в ЦАГИ, ЦИАМ, ВВА им. Н.Е.Жуковского. В 1947 году Д.Ю.Панов возглавил вновь организованный физико - технический факультет МГУ, который затем был преобразован в Московский физико-технический институт.

 

Обширно и разнообразно по тематике научное наследие Д.Ю.Панова. Он является автором более 70 работ, посвященных конструированию машин и приборов, авиационным расчетам, численным методам решения дифференциальных уравнений.

 

Среди работ Д.Ю.Панова, относящихся к задачам теории и практики приближенных вычислений, следует отметить ряд статей, посвященных приближенному численному решению различных классов уравнений математической физики. В этих статьях дается ряд усовершенствований метода сеток, метода С.А.Чаплыгина, а также предлагаются новые практические методы решения различных уравнений с частными производными.

 

Среди работ Д.Ю. Панова, посвященных авиационной прочности, центральное место занимают исследования по расчету воздушного винта на прочность. Занявшись этим вопросом, Д.Ю.Панов, поставил себе цель, опираясь на прежние теории, дать такой метод расчета, который мог бы быть использован в конструкторских бюро. В результате своих исследований Д.Ю.Панов впервые предложил систему интегро-дифференциальных уравнений, к которой сводится задача о равновесии лопасти воздушного винта в полете, и указал практические методы ее решения, а также привел ряд примеров расчета, доведенных до окончательных численных результатов и могущих быть непосредственно использованными на производстве. Для проверки правильности допущений, которые были сделаны при решении этой задачи, Д.Ю.Панов организовал ряд экспериментальных работ. Им был, кроме того, предложен оригинальный прибор для записи деформаций и вибраций в полете, построенный в ЦАГИ. Исследования в этих направлениях развивали в тесном контакте с ЦАГИ сотрудники кафедры Б.П.Демидович, Б.О.Солоноуц, А.Р.Янпольский.

 

Несколько работ Д.Ю.Панова по ремонту воздушных винтов, выполнены в военное время по заданию ВВС Красной Армии. Эти работы впервые дали научные основания проблеме обеспечения прочности лопастей воздушных винтов, отремонтированных в полевых условиях, и завершились выпуском инструкции по полевому ремонту винтов, принятой в частях.

 

Большая группа работ Д.Ю. Панова посвящена вопросам теории точных приборов, их конструкции и расчета. В этих работах Д.Ю.Панов занимался наиболее трудными проблемами приборостроения, связанными с расчетом элементов, требующих решения нелинейных задач (тонкие пластинки при больших прогибах, гофрированные мембраны, биметаллические оболочки, элементы, рассчитываемые с учетом гистерезиса). В 1929 – 1932г. Д.Ю.Пановым была спроектирована и построена машина для автоматического нанесения защитных розеток на формы для печатания денежных знаков. На эту машину Д.Ю.Панову было выдано авторское свидетельство. А в 1934году Д.Ю.Панов получил авторское свидетельство на автоматическую машину для измерения площади, определения объема и отметки толщины кожи. Соответствующий проект получил высшую премию на всесоюзном конкурсе.

 

Среди работ Д.Ю.Панова по теории упругости следует отметить замечательные работы по кручению непризматических стержней, в которых автор весьма остроумным методом дал решение этой задачи для тех случаев, которые наиболее интересны практически: для кручения стержня, близкого к призматическому при произвольном виде поперечного сечения стержня. Кроме того, в ряде работ даны новые решения задач об изгибе и кручении некоторых профилей. Эти результаты были использованы также в теории прочности винта.

 

Д.Ю.Панов награжден орденами «Трудового красного знамени» и «Красной Звезды», а также медалями.

 

В 1936-1941 гг. кафедрой заведовал Лев Абрамович Тумаркин (1904-1974). У нас в стране и за рубежом он известен своими работами в области топологии, и прежде всего по теории размерности, которые публиковались, начиная с 1925 года. Одним из его наиболее важных результатов является решение поставленной П.С.Урысоном проблемы о возможности разбиения компакта n-мерным подкомпактом. Л.А. Тумаркин показал, что все основные факты теории размерности, установленные в категории компактов, справедливы и вне этой категории, поскольку найденные им доказательства не используют условий компактности, а требуют лишь метризуемости пространства и наличия в нем счетной базы.

 

С 1936 по 1948 гг. на кафедре работал доцент (в последствие профессор) Борис Павлович Демидович (1906-1977). Основными направлениями его научной деятельности были математический анализ, качественная теория обыкновенных дифференциальных уравнений и математическая физика. В своих работах (их у него около шестидесяти) Б.П.Демидович исследовал  динамические системы с интегральными инвариантами, периодические и почти периодические решения, ограниченные решения обыкновенных дифференциальных уравнений, правильные и вполне правильные  дифференциальные системы, устойчивость обыкновенных дифференциальных уравнений, в частности, орбитальную устойчивость динамических систем.

 

Чрезвычайно плодотворной была учебно-методическая деятельность Б.П.Демидовича. С 1927 по 1931 годы он работал учителем математики в ряде средних учебных заведений Брянской и Смоленской областей, с 1932 по 1934 годы – в Транспортно-экономическом институте НКПС, в 1935 году – в Институте кожевенной промышленности. С 1936 по 1977 годы Б.П.Демидович – бессменный сотрудник кафедры математического анализа механико-математического факультета МГУ. Наряду с научно-педагогической деятельностью в МГУ Б.П.Демидович по совместительству преподавал в ряде ведущих вузов Москвы (кроме МВТУ им. Н.Э.Баумана отметим Военно-инженерную академию им. Ф.Э.Дзержинского). Он читал лекции по общим и специальным курсам высшей математики, консультировал аспирантов, участвовал в организации математических олимпиад. Б.П.Демидович – автор многочисленных учебников и сборников задач по математическому анализу, вычислительной математике, математической теории устойчивости.

 

Б.П.Демидович активно сотрудничал с редакциями различных математических изданий («Дифференциальные уравнения», РЖ «Математика»), а также с «БСЭ».

 

С 1930 по 1947 годы на кафедре работал кандидат физико - математических наук, доцент Борис Осипович Солоноуц (1907 - 1975). Наряду с научными исследованиями, посвященными нахождению точного решения задачи кручения для несимметрических областей, он вел большую организационную работу. Был начальником учебно-методического сектора, ученым секретарем кафедры. Работал в комитете по Сталинским премиям в области науки и изобретательства при СНК СССР (военных изобретений, спец. секции, технические науки). После ухода из МВТУ Б.О.Солоноуц работал в МФТИ и Новосибирском государственном университете (деканом факультета естественных наук).

 

Около двадцати лет на кафедре «Высшая математика» работал кандидат физико - математических наук, доцент Анатолий Николаевич Тулайков (1907 – 1991). Он известен своими исследованиями, посвященными оценкам для коэффициентов степенного ряда, компактности в банаховых пространствах, условиям нормальности семейств потенциальных функций, а также как автор сборника задач по элементарной математике.

 

После ухода из МВТУ (в 1949 году) А.Н.Тулайков преподавал в МФТИ, был начальником учебной части института, а также заместителем председателя методической комиссии по математике.

 

С 1930 по 1948 годы на кафедре работал кандидат физико – математических наук, доцент Янпольский Авраам Рувимович (1905-1978). Его научные интересы лежали в области прикладной механики. В частности, диссертация А.Р.Янпольского посвящена кручению анизотропных призматических стержней с длинным и узким поперечным сечением. Другие работы А.Р.Янпольского посвящены движению глиссирующей пластины в плоско – параллельном потоке, а также проблемам гидродинамического подобия.

 

А.Р.Янпольский – автор учебных пособий по математическому анализу, дифференциальным уравнениям, гиперболическим функциям, степенным рядам, сборников задач по элементарной математики для абитуриентов.

 

После ухода из МВТУ А.Р.Янпольский работал в военно-инженерной академии им. В. В. Куйбышева.

---

 

Преподаватели кафедры «Высшая математика» МВТУ им. Н. Э. Баумана на фронтах Великой Отечественной Войны

 

22 июня 1941 г. в МММИ им. Н.Э. Баумана по сложившейся традиции проводился день открытых дверей, где сотрудники, студенты и абитуриенты узнали о начале Великой Отечественной войны. В начале июля началась запись добровольцев в 7-ю дивизию народного ополчения Бауманского района. В переполненной 327-й аудитории прошел митинг, после которого в течение нескольких часов шла запись добровольцев (всего более 500 человек). Среди них были преподаватели кафедры «Высшая математика» доцент Сергей Васильевич Фролов и ассистент Серафим Федорович Шурлапов.

 

С.В.Фролов и С.Ф.Шурлапов были зачислены в 76 артбатарею 20 стрелкового полка Бауманской дивизии. С.В.Фролов был назначен командиром орудия, а С.Ф.Шурлапов – командиром взвода. Среди ополченцев были люди в возрасте от 18 до 35 лет. Основная масса младших и средних командиров боевым опытом не обладала. Командиром 76 батареи был музыкант.

 

Бойцам выдали кавалерийские карабины и трехдюймовки, но стрелять почти никто не умел. С. В. Фролов и С. Ф. Шурлапов составили на основе логарифмических таблиц таблицы стрельбы на основные расстояния.

 

9 июля Бауманская дивизия выступила из Москвы в район Химок, где начала боевую учебу. Основной упор делался на строевую, противохимическую и политическую подготовку. Хуже дело обстояло непосредственно с боевой подготовкой из-за недостатка боеприпасов. Бойцы 76 артбатареи учились стрелять из винтовки, на каждого было по четыре патрона. Удалось провести учебную стрельбу из орудий, было выпущено два снаряда.

 

В конце июля 32-я армия, в которую была включена Бауманская дивизия, получила задачу сосредоточиться в районе Вязьмы, чтобы к 4 августа занять рубеж Богородское – Лысово – Подрезово – Панфилово – Годуновка. До Волоколамска бойцы 76 артбатареи шли пешком, а до Вязьмы доехали на поезде. Заняв позиции во втором эшелоне, бойцы Бауманской дивизии занялись строительством оборонительных сооружений.

 

30 сентября 1941 г. немецкие танковые дивизии начали операцию «Тайфун». Оборона наших войск была прорвана, 6 октября враг занял Вязьму. Бауманская дивизия оказалась в окружении. Получили приказ отступать. Все дороги, леса были заполнены отступающими солдатами, повозками. Кто шел пешком, кто ехал на машинах. Подразделения дивизии предпринимали попытки вырваться из окружения. При одной из таких попыток С.В.Фролов и С. Ф. Шурлапов были ранены осколками разорвавшейся мины и не могли идти дальше. С. В. Фролов был ранен в ногу, а С. Ф. Шурлапов в спину. Немцы стали прочесывать лес с собаками и обнаружили спрятавшихся в окопе красноармейцев. Их поместили в ближайшей деревне Селище, в одной крестьянской избе. Через полторы недели С.В. Фролов мог ходить с помощью палки. Он стал помогать хозяйке избы, пытался лечить своих раненых товарищей. Однако ранение С. Ф. Шурлапова было очень тяжелым. 27 октября 1941 г.  он скончался и был похоронен на кладбище села Никольское.

 

Уроженец города Тулы, выпускник электротехнического факультета МВТУ (на правах вольнослушателя), С. Ф. Шурлапов начал преподавательскую деятельность на кафедре «Высшая математика» в 1930 г. Он зарекомендовал себя прекрасным преподавателем и методистом. Принял участие в создании трехтомного задачника по высшей математике (задачник вышел в 1944 году). Прекрасно стрелял, был Ворошиловским стрелком, участвовал в различных соревнованиях и вел стрелковую секцию в нашем ВУЗе.

 

С.В.Фролов был помещен в лагерь в городе Юхнов, а через некоторое время его отправили в более крупный лагерь в Кричев. Пленные возили кирпичи, бревна, валили лес. Надзор осуществлял конвой из украинских националистов и русских полицаев. Немецкий гарнизон пьянствовал.

 

Пленным удалось установить связь с партизанами. Вскоре С.В.Фролову с несколькими товарищами удалось бежать. Группа пленных под видом рабочей команды пошла на станцию, и, дождавшись подходящего момента, они свернули с дороги в кусты, где их ждал проводник от партизан. Пришли в деревню, которая не была занята немцами и где была передовая разведка четвертой Клетнянской партизанской бригады. Однако на следующий день немцы окружили эту деревню. Партизанам пришлось прорываться из окружения. В бою С.В. Фролов был ранен в руку. Через три дня беглецы оказались в расположении основного отряда.

 

Из-за ранения С.В. Фролов долго не мог принимать участие в боевых действиях. Первое время он пас коров, которых партизаны отбили у немцев. Потом его стали отправлять в разведку. Пригодилось знание немецкого языка: он выполнял обязанности переводчика. Допрашивал немцев, которые попадали в плен к партизанам.

 

Позже во время отступления фашистов С.В.Фролов вместе со своей партизанской бригадой отправился дальше на запад. Немцы отступали так быстро, что партизаны не успевали идти впереди них. И в брянских лесах партизанская бригада встретила Советскую Армию. С.В.Фролов оказался в составе 31 дивизии 11 гвардейской армии генерала И.Х.Баграмяна.

 

До конца войны дослужить не удалось, так как в 1944 г. вышел приказ о демобилизации специалистов. С.В.Фролов вернулся в МВТУ им. Н.Э. Баумана на свою кафедру «Высшая математика».

 

В октябре 1941 года Правительство СССР приняло решение об эвакуации из столицы НИИ, вузов и учреждений культуры. МММИ им. Н.Э.Баумана направлялся в Ижевск, где ему предоставили вначале здание ремесленного училища, которое практически не годилось для чтения лекций и проведения лабораторных работ. Спустя несколько месяцев МММИ был переведен в более приспособленное для учебы бывшее здание педагогического института. 10 ноября 1941 года здесь возобновились занятия на первых трех курсах, а с 8 декабря — на старших курсах. Все студенты ежедневно по 11 часов работали на оборонных предприятиях, а занятия начинались поздно вечером. За короткий срок многие из них успешно освоили рабочие профессии, затем стали работать в технологических бюро и на заводах. Преподаватели также трудились на производстве, как правило, внедряя свои разработки. Кроме того, коллектив МММИ им. Н.Э. Баумана проводил культурно-массовую работу в госпиталях Ижевска. Среди преподавателей математики, эвакуированных в Ижевск, были доценты Б.О.Солоноуц и В.А.Ефименко.

 

В марте 1942 года в Москве начал работать филиал МММИ им. Н.Э.Баумана, в котором обучались оставшиеся в Москве по различным причинам студенты, ранее учившиеся как в МММИ и других втузах. Началась ускоренная подготовка специалистов со сроком обучения четыре года вместо пяти с половиной лет. Обязанности заведующего кафедрой «Высшая математика» московского филиала исполнял доцент Б.П.Демидович. В этот период преподаватели кафедры подготовили к изданию задачник по высшей математике в трех частях. В работе над задачником приняли участие Г.С.Бараненков, И.П.Ветчинкин, Б.П.Демидович, Г.Л.Лунц, Е.П.Сычева, С.В.Фролов, С.Ф.Шурлапов, А.П.Юшкевич, А.Р.Янпольский.

 

Весной 1943 года коллектив училища вернулся из Ижевска в Москву. В этом же году постановлением ГКО СССР Институту присвоено название «Московское высшее техническое училище имени Н.Э. Баумана».

 

В послевоенные годы кафедра «Высшая математика» пополнилась преподавателями, которые принимали участие в боях за Родину. Среди них доценты Е.Н.Мирославлев, Я.Г.Ковалев, Г.И.Богомолов, К.К.Василевский, ассистенты Е.Б.Пасько и С.М.Коган.

---

 

Московское высшее техническое училище имени Н.Э. Баумана

 

С 1943 по 1989 годы наш университет назывался Московским высшим техническим училищем (МВТУ) имени Н.Э. Баумана. Под этим названием он вошел в советскую и российскую историю и стал известен во многих странах мира, в особенности после запуска в 1957 году первого искусственного спутника Земли, в разработке которого принимали участие выпускники МВТУ. Многие в нашей стране и за рубежом знали и знают «Бауманку» как «кузницу» высококлассных инженеров для ракетно-космической отрасли и крупный научно-технический центр но исследованиям и разработкам в области оборонной и ракетно-космической техники. МВТУ им. Н.Э. Баумана продолжало поддерживать и развивать основные положения «русского метода обучения», разработанного еще в XIXвеке.

 

Переименование МММИ в МВТУ им. Н.Э. Баумана произошло в соответствии с Постановлением Государственного Комитета Обороны СССР в мае 1943 года. Этим же постановлением на МВТУ им. Н.Э. Баумана возлагалась подготовка инженеров широкого профиля. Срок обучения в нем увеличивался до пяти с половиной лет. Проректор по научной работе Г.А.Николаев (впоследствии ректор), возглавлявший работу по реализации указанного постановления, позже вспоминал: «Под инженером широкого профиля мы понимали глубокую подготовку по фундаментальным дисциплинам. Кроме того, каждый выпускник в своей специальности должен был владеть методами инженерных расчетов, проектирования, основными технологическими процессами, условиями испытаний и эксплуатации разрабатываемых машин, выпускник также должен владеть основами и методиками проведения научных исследований».

 

С 1930 года на кафедре «Высшая математика» работал, а в период 1941-1952 гг. заведовал кафедрой доктор физико - математических наук, профессор Адольф (Андрей) Павлович Юшкевич (1906-1993) — видный историк математики, инициатор издания трудов многих классиков математики, один из основателей и ответственный редактор сборников "Историко-математические исследования", президент Международной академии истории науки (1965-1968). Он много сделал для установления тесных научных и методических связей кафедры «Высшая математика» МВТУ с ведущими математическими кафедрами вузов страны, что способствовало высокому уровню научных исследований и преподавания математики в училище.

 

В 1953-1956 гг. кафедру «Высшая математика» возглавлял доктор технических наук, профессор Кирилл Петрович Станюкович (1916-1989), выдающийся физик-теоретик, астроном, газодинамик, заслуженный деятель науки и техники РСФСР. Всего им опубликовано более шестисот научных работ. Он занимался проблемами метеорной астрономии, кратерообразования на Луне и планетах, вопросами гравитации, космогонии и космологии. В области газовой динамики изучал неустановившиеся движения сплошной среды, взрывные явления, проблемы космической газодинамики. В области теоретической физики - теорию гравитации и элементарных частиц. Его работы сыграли заметную роль в развитии ряда научных направлений в газовой динамике, теории детонации, релятивистской механике сплошной среды, а также в развитии российской оружейной науки.

 

В 1957-1959 гг. кафедрой «Высшая математика» заведовал доктор технических наук, профессор Иван Александрович Паничкин (1914-1970), специалист в области прикладной газодинамики, заслуженный деятель науки и техники. И.А.Паничкин – автор ряда работ, посвященных вопросам обтекания тел вращения высокоскоростным воздушным потоком. Среди его трудов – монография "Теория одномерного движения газа и её приложения к газодинамическому расчету сверхзвуковых аэродинамических труб".

 

В конце 1940-х-начале 1950-х годов на кафедре высшей математики сложился коллектив преподавателей высокого класса. В штате кафедры было более 25 преподавателей, среди них профессор П.М.Риз, доценты С.В.Фролов, Р.Я.Шостак, В.А.Ефименко, Е.А.Лубны-Герцык, Г.С.Бараненков, Е.П.Сычева, Е.Н.Мирославлев, Г.Л.Лунц, Н.М.Коробов, А.Н.Тулайков, М.И.Ершова, С.И.Савельев, М.З.Осипова, ассистенты Н.Н.Бурмистрова, С.М.Коган, В.А.Калашников, Е.Ф.Поршнева, Л.З.Юделевич, Е.Б.Пасько, С.Л.Черемшанский, Н.А.Золотухин, Н.В.Сахаров, Е.А.Соболева, В.А.Тарасова, Н.Н.Щетинина К.Г.Лобова, Л.П.Макарова.

 

 

Накопленные на кафедре в процессе преподавания методические материалы после тщательного отбора и длительной апробации использовались в многочисленных учебных пособиях для студентов. В частности, опыт ведения практических занятий по математике был обобщен в изданном в 1944 году в МВТУ «Задачнике по высшей математике», на основе которого был составлен в 1959 году под редакцией Б.П.Демидовича сборник «Задачи и упражнения по математическому анализу для втузов». Сборник содержал более 3000 задач по всем основным разделам втузовского курса математического анализа: теории пределов, дифференциальному и интегральному исчислению функций одной и нескольких переменных, теории рядов, дифференциальным уравнениям. С ответами, методическими указаниями и решениями типовых примеров. Этот задачник переиздавался более тридцати раз, был переведен на французский, испанский и португальский языки. Его авторами были преподаватели, в разное время работавшие на кафедре «Высшая математика» МВТУ: Г.С.Бараненков, Б.П.Демидович, В.А.Ефименко, С.М.Коган, Г.Л.Лунц, Е.Ф.Поршнева, Е.П.Сычева, С.В.Фролов, Р.Я.Шостак, А.Р.Янпольский.

 

Длительный период методического совершенствования математической подготовки студентов МВТУ был отражен в написанном С.В.Фроловым и Р.Я.Шостаком «Курсе высшей математики», выпущенном двумя изданиями (в 1966 г. и 1973 г.). В этом учебнике просто и доступно изложены все основные разделы высшей математики, изучаемые в технических вузах: векторная алгебра и аналитическая геометрия, теория пределов, дифференциальное и интегральное исчисление функций одной и нескольких переменных, теория поля, числовые, степенные и тригонометрические ряды, дифференциальные уравнения, элементы теории вероятностей.

 

В 1968 году вышло учебное пособие Р.Я.Шостака по операционному исчислению.

Доцент Фролов Сергей Васильевич (1906-1980), кандидат физико-математических наук, проработал на кафедре более сорока лет. В середине 1960-х годов исполнял обязанности заведующего кафедрой высшей математики.

 

Научные работы С.В.Фролова посвящены критическим значениям функций, заданных на многообразиях. Кроме того,  С.В.Фролов принял участие в создании учебника по высшей математике и нескольких сборников задач.

С.В.Фролов - участник Великой Отечественной войны. Кавалер многочисленных наград, среди которых медали за победу над Германией в Великой Отечественной войне, за оборону Москвы.

Доцент Шостак Родион Яковлевич (1902-1981), кандидат физико-математических наук, работал на кафедре «Высшая математика» с 1938 по 1971 годы. Был заместителем заведующего кафедрой.

Р.Я.Шостак - автор ряда научных работ различной тематики: «О сравнительной точности формул механических квадратур Ньютона-Котеса с четным и нечетным числом ординат», «О формулах механических квадратур с кратными узлами», «Интегрирование линейных дифференциально-разностных уравнений методом разложения операторов в бесконечные ряды», «О главной части остаточного члена формулы Тейлора», «О производных с произвольным указателем порядка дифференцирования от аналитических функций комплексного переменного».

 

В своей работе «Алексей Васильевич Летников» Р.Я.Шостак изложил подробную биографию выдающегося ученого, а также провел исследование научного наследия А.В.Летникова.

Обширно учебно – методическое наследие Р.Я.Шостака. Он принял участие в создании задачника по математическому анализу, учебника по высшей математике, пособий по операционному исчислению, теории рядов, теории функций комплексной переменной.

Кроме МВТУ им. Н.Э.Баумана Р.Я.Шостак работал консультантом по математике в Ленинской библиотеке, а также в Московском статистическом управлении.

 

 

Доцент Ефименко Валентина Афанасьевна (1906-1986), кандидат физико-математических наук, после окончания аспирантуры механико-математического факультета МГУ работала в Математическом институте им. В.А.Стеклова. Ей принадлежит ряд научных работ, посвященных приближенному вычислению собственных значений и собственных функций краевых задач дифференциальных уравнений различных видов.

 

С 1934 по 1973 годы В.А.Ефименко работала на кафедре «Высшая математика» МВТУ, в течение нескольких лет была заместителем заведующего кафедрой. Приняла участие в создании сборника задач по математическому анализу.

 

С 1934 по 1952 годы на кафедре высшей математики работал кандидат физико – математических наук, доцент Лунц Григорий Львович (1911-1977).

 

Научные интересы Г.Л.Лунца были сосредоточены в области комплексного анализа. Он был специалистом по теории рядов Дирихле, которые связаны с различными интегральными преобразованиями, дифференциальными уравнениями, специальными классами функций. В большом цикле работ, посвященных рядам Дирихле, автор получил глубокие результаты относительно областей сходимости таких рядов, особенностей их сумм, их приложений к теории целых функций.

 

Другим направлением научной деятельности Г.Л.Лунца было исследование творчества Николая Ивановича Лобачевского. Ряд статей Г.Л.Лунца посвящены работам Н.И.Лобачевского по интегральному исчислению, теории рядов, гамма - функциям. Г.Л.Лунц является автором вводных статей и комментариев к ряду работ Н.И.Лобачевского в полном собрании его сочинений.

 

Обширно методическое наследие Г.Л.Лунца. Он является автором учебников и методических пособий по теории функций комплексного переменного, теории вероятностей, операционному исчислению. Также Г.Л.Лунц принял участие в создании сборника задач по математическому анализу и краткого физико – технического справочника. Эти книги были переведены на английский, французский, испанский и другие языки, были изданы в Англии, США, Китае, Японии, Бразилии, Чехословакии.

 

После ухода из МВТУ Г.Л.Лунц работал в ряде высших учебных заведений, среди которых Московский институт химического машиностроения, где он заведовал кафедрой высшей математики. В 1963 году Г.Л.Лунц защитил докторскую диссертацию на тему «Ряды Дирихле с комплексными показателями и ряды Тейлора – Дирихле» и был утвержден в ученом звании профессора.

 

Г.Л.Лунц был членом научно – методического совета по математике Минвуза СССР, членом программной комиссии и комиссии по учебной литературе. Он принимал активное участие в разработке втузовской программы по математике.

 

Г.Л.Лунц – участник Великой Отечественной войны.

С 1931 по 1964 годы на кафедре работала доцент Сычева Елена Павловна (1908-1965), кандидат физико – математических наук. Ей принадлежит ряд научных работ в области высшей геометрии и топологии. В частности, Е.П.Сычева построила достаточно полную систему инвариантов компактного топологического пространства, включающую все ранее известные инварианты гомологического типа. Сверх того, она получила ряд новых инвариантов и исследовала для них вопрос о теоремах двойственности.

 

Также Е.П.Сычева приняла участие в создании задачников по математическому анализу.

 

С 1949 по 1951 годы Е.П.Сычева работала в Монголии, в Государственном университете Улан-Батора, заведовала кафедрой высшей математики и была деканом педагогического факультета.

 

Более тридцати лет на кафедре «Высшая математика» работала старший преподаватель Поршнева Екатерина Федоровна (1903-1978). Она приняла участие в создании задачника по математическому анализу.

 

Е.Ф.Поршнева была разносторонне одаренным человеком. Она была членом литературного объединения при редакции газеты «Бауманец», писала замечательные стихи.

 

Доцент Бараненков Георгий Сергеевич, кандидат педагогических наук, проработал на кафедре «Высшая математика» более тридцати лет. Его диссертация посвящена организации и методике преподавания математики в заочном высшем техническом учебном заведении.

 

Г.С.Бараненков был методистом высшего уровня. Он принял участие в создании ряда сборников задач по математическому анализу, а также методического пособия по аналитической геометрии. В середине 1960-х годов, будучи опытным преподавателем, Г.С.Бараненков брал шефство над молодыми ассистентами, пришедшими на кафедру сразу после окончания института. Он помогал им в составлении плана занятий, посещал их семинары, а также давал рекомендации, как лучше объяснить студентам наиболее трудные разделы курса высшей математики.

 

Старший преподаватель Коган Сергей Михайлович (1916-1992) работал на кафедре «Высшая математика» с 1948 по 1973 годы. С 1973 по 1984 годы – на кафедре «Прикладная математика». Он принял участие в создании задачника по математическому анализу, а также методического пособия по теории функций комплексной переменной.

 

С.М.Коган – участник Великой Отечественной войны. Он воевал в артиллерийском подразделении четвертой ударной армии. Был награжден медалями.

 

С.М.Коган был кандидатом в мастера спорта по шахматам. Он неоднократно принимал участие в различных турнирах.

Ассистент Николай Васильевич Сахаров пришел на кафедру еще в 1921 году и проработал около сорока лет. В 1927 году им был составлен задачник по алгебре для абитуриентов. Н.В.Сахаров – автор ряда работ, посвященных интегрированию дифференциальных уравнений Риккати. В 1957 году, будучи одним из старейших сотрудников кафедры (ему было 68 лет), Н.В.Сахаров написал очерк по истории кафедры высшей математики за период 1920-1956 годы. Материалы этого очерка использованы в данной работе.

 

С 1946 по 1961 годы на кафедре «Высшая математика» работал доктор физико - математических наук, профессор Петр Михайлович Риз (1906-1990). Он занимался такими проблемами, как вопросы прочности в самолетостроении, теория случайных процессов, фундаментальные проблемы теории упругости. Среди его работ отметим следующие: «Определение собственных частот вибраций лопастей воздушных винтов», «Деформации и напряжения естественно закрученных стержней», «К асимптотическому интегрированию уравнений теории упругости в применении к пластинкам и дискам переменной толщины».

 

П.М.Риз долгое время читал лекции для аспирантов и сотрудников института по различным разделам математики и механики, как, например, «Теория случайных процессов», «Теория нелинейных колебаний», «Исследование операций», «Методы функций в гидро- и аэродинамике».

 

В конце 1940-х – начале 1950-х годов на кафедре вели занятия (преимущественно по совместительству) ряд математиков, основная деятельность которых была связана с другими научными и учебными институтами.

 

Доцент Арсенин Василий Яковлевич (1915-1990), специалист в области математической физики, в 1937 году окончил Московский пединститут им. К. Либкнехта. Далее учился в аспирантуре у П.С. Новикова. Первые научные работы, посвященные вопросам теории множеств, легли в основу его кандидатской диссертации. После войны В. Я. Арсенин работал в МИФИ, в Институте прикладной математики АН СССР, а также в МВТУ им. Н. Э. Баумана (по совместительству). В 1970 г. В. Я. Арсенин защитил докторскую диссертацию, в 1972 г. ему присвоено звание профессора.

 

В своей научной деятельности В. Я. Арсенин плодотворно занимался разработкой методов решения задач математической физики. Последние годы его научные интересы были сосредоточены в области решения некорректных задач вычислительной диагностики.

 

В. Я. Арсенин – автор более ста научных работ. Ему принадлежат учебные пособия и монографии, посвященные методам математической физики, специальным функциям, задачам компьютерной томографии, методам решения некорректных задач.

 

В. Я. Арсенин принимал активное участие в ряде крупных исследований, имеющих большое народнохозяйственное значение. В 1984 г. ему была присуждена Государственная премия СССР за создание базовой конструкции ряда рентгеновских томографов и разработку единой системы их математического обеспечения (в составе коллектива авторов).

 

В. Я. Арсенин – участник Великой Отечественной войны. Награжден боевым орденом «Красной Звезды» и медалями.

 

Ассистент Жидков Николай Петрович (1918 - 1993) работал на кафедре «Высшая математика» МВТУ им. Н. Э. Баумана с 1947 по 1949 годы. В 1949 году защитил кандидатскую диссертацию на тему «Дискретные динамические системы». С 1949 по 1993 годы работал в МГУ им. М. В. Ломоносова (до 1970 года доцент кафедры вычислительной математики механико-математического факультета, а с 1970 по 1993 годы -  доцент кафедры вычислительной математики, затем математической физики факультета ВМК).

 

Н. П. Жидков принимал активное участие в организации учебной и научной работы кафедры вычислительной математики механико-математического факультета, создании курса лекций по методам вычислений, в постановке практикумов. Внес большой вклад в формирование научной тематики Вычислительного центра МГУ, в течение ряда лет заведовал лабораторией теоретических исследований ВЦ. В 1970 году Н. П. Жидков перешёл на только что созданный факультет вычислительной математики и кибернетики.

 

Н. П. Жидков - автор около 120 научных работ по численным методам, оптимизации, распознаванию образов, математическим методам в кристаллографии. Он принимал участие в решении прикладных задач космонавтики, ядерной физики, гидродинамики, структурного анализа кристаллов. Широко известны монографии и учебники: Бахвалов Н. С., Жидков Н. П., Кобельков Г. М. «Численные методы», Березин И. С., Жидков Н. П. «Методы вычислений», Жидков Н. П. «Линейные аппроксимации функционалов», Жидков Н. П., Щедрин Б. М. «Геометрия кристаллического пространства».

 

Н. П. Жидков - ветеран войны с Финляндией и Великой Отечественной войны. Участвовал в боях на Ленинградском и Третьем Прибалтийском фронтах, был семь раз ранен. Награждён орденами Отечественной войны II и I степени, орденом Красной Звезды и многими медалями.

 

Доцент Коробов Николай Михайлович (1917 – 2004), кандидат физико-математических наук, работал на кафедре «Высшая математика» МВТУ им. Н. Э. Баумана по совместительству. В 1953 году защитил докторскую диссертацию на тему «Об арифметических свойствах показательных функций». Профессор кафедры теории чисел механико-математического факультета МГУ им. М. В. Ломоносова.(1956–2004).

 

Научные интересы Н. М. Коробова лежали в области теории чисел и вычислительной математики. Ему принадлежат более шестидесяти научных работ, посвященных вопросам распределения дробных долей, оценкам тригонометрических сумм, приближенному вычислению кратных интегралов. Среди его работ монографии «Теоретико-числовые методы в приближенном анализе» (1963) и «Тригонометрические суммы и их приложения» (1989).

 

Ассистент Полосуев Александр Михайлович (1925 – 2003) преподавал на кафедре «Высшая математика» МВТУ им. Н. Э. Баумана с 1951 по 1955 годы. Он вел научные исследования в области равномерного распределения дробных долей функций. В 1959 году защитил кандидатскую диссертацию на тему «Многомерные задачи теории диофантовых приближений с показательными функциями». Доцент кафедры математического анализа мехмата МГУ им. М. В. Ломоносова (1961–2003). Преподавал высшую математику на химическом факультете МГУ.

 

А.М.Полосуев был членом Научно-методического совета при MB и ССО СССР. Под его руководством комиссия, составленная из преподавателей математики и химии, подготовила типовую программу по математике для химических факультетов университетов СССР. В течение 10 лет возглавлял первичную организацию общества «Знание» на мехмате МГУ, принимал активное участие в пропаганде математических знаний. Многократно выступал в школах и техникумах Москвы, Курска, Махачкалы и других городов.

 

С 1952 по 1954 год на кафедре «Высшая математика» МВТУ им. Н. Э. Баумана работал доцент Лев Анатольевич Скорняков (1924-1989). С 1954 года он работал на кафедре высшей алгебры мехмата МГУ им. М. В. Ломоносова. В 1958 году защитил докторскую диссертацию и был утвержден в звании профессора.

 

 

Круг научных интересов Л. А. Скорнякова был необычайно широк. Его работы по теории проективных плоскостей, теории структур, теории колец, по абелевым группам и модулям, по гомологической алгебре, по логическим аспектам в алгебраических системах, стохастической алгебре и выпуклому анализу получили широкую известность среди специалистов. Результаты этих исследований оказали значительное влияние на развитие ряда разделов современной алгебры.

 

Среди работ Л.А. Скорнякова монографии и учебные пособия «Дедекиндовы структуры с дополнениями и регулярные кольца», «Абелевы группы и модули», «Элементы теории структур», «Элементы общей алгебры», «Элементы алгебры». Он был членом проблемной комиссии по алгебре при АН СССР, членом редколлегии журнала «Математический сборник». Возглавлял редколлегию межвузовского сборника «Абелевы группы и модули».

 

Л. А. Скорняков - участник Великой Отечественной войны, был артиллеристом. В марте 1943 года в бою при поселке Красный бор (Ленинградский фронт) он был ранен, в результате ранения он потерял левую руку. Был награжден медалями «За отвагу», «За победу над Германией».

 

Ассистент Агамалов Александр Степанович, автор ряда учебных пособий по криволинейным интегралам, теории вероятностей и ее применениям в расчетах надежности, преподавал в МВТУ им. Н.Э. Баумана с 1950 по 1952 годы. На протяжении многих лет он работал во Всесоюзном заочном электротехническом институте связи.

 

Выпускник МГПИ им. В. И. Ленина Иван Тимофеевич Бородуля известен своими методическими пособиями для учителей: «Показательная и логарифмическая функции», «Тригонометрические уравнения и неравенства», «Показательные и логарифмические управления и неравенства».

 

В течение ряда лет И. Т. Бородуля работал учителем математики в физико-математической школе №2, а также методистом РОНО Октябрьского района г. Москвы.

 

Константин Андреевич Карачаров, кандидат физико-математических наук, преподавал на кафедре «Высшая математика» МВТУ им. Н. Э. Баумана с 1951 по 1953 годы. Он является автором ряда учебных пособий по теории устойчивости движения. В течение многих лет К. А. Карачаров работал в Московском лесотехническом институте.

 

Ассистент Срагович Владимир Григорьевич работал на кафедре «Высшая математика» МВТУ им. Н. Э. Баумана с 1953 по 1956 годы. Вел научные исследования по теории самонастраивающихся систем. В 1957 году В. Г. Срагович защитил в вычислительном центре АН СССР кандидатскую диссертацию на тему «Синтез адаптивных управляющих систем в виде автоматов». Автор ряда монографий, среди которых отметим следующие: «Теория адаптивных систем» (1976), «Адаптивное управление» (1981),  «Управление и адаптация» (1985).

 

Упомянем также доцента Кузнецова Дмитрия Сергеевича, автора пособий «Специальные функции», «Операционное исчисление», а также  ассистента Ратникову Раису Дмитриевну, которая была медсестрой ЭГ-268 Ленинградского, затем II Белорусского фронта. Р. Д. Ратникова награждена орденом Отечественной войны II степени, медалями «За боевые заслуги», «За оборону Ленинграда», «За Победу в Великой Отечественной войне». В 1948 году она окончила математико-механический факультет ЛГУ по специальности «механика». Преподавала математику в МВТУ им. Н. Э. Баумана, Ленинградском Политехническом институте, Ленинградском институте инженеров железнодорожного транспорта.

 

С 1953 по 1987 годы на кафедре высшей математики работала Герой Советского Союза Евдокия Борисовна Пасько. В 1938 году она поступила на мехмат МГУ, но с четвёртого курса университета ушла добровольцем в армию. Окончила ускоренные штурманские курсы в авиационной школе города Энгельс. В действующей армии с мая 1942 года. С июля 1943 года Е.Б.Пасько – штурман эскадрильи, а с ноября 1944 года – помощник командира полка по воздушно – стрелковой службе.

 

 

Е.Б.Пасько совершила 790 боевых вылетов и 10 вылетов на спецзадания. Общий налёт составил 1220 часов. На позиции врага было сброшено более 100 тонн бомб. Е.Б.Пасько уничтожила несколько складов с горючим и боеприпасами, прожектора, переправы, 11 автомашин и 1 самолёт на земле. Кроме того, в тылу противника она сбросила до 2 миллионов листовок.

 

Е.Б.Пасько была награждена медалью «Золотая Звезда», орденом Ленина, орденом Боевого Красного Знамени, двумя орденами Красной Звезды, двумя орденами Отечественной войны первой степени, орденом Дружбы Народов.

 

В конце 1945 года гвардии старший лейтенант Е.Б.Пасько вышла в отставку. Вернулась к учебе и успешно окончила последние курсы мехмата МГУ, а затем аспирантуру кафедры теории упругости. На кафедре высшей математики МВТУ Е.Б.Пасько читала лекции и вела семинарские занятия по всем разделам общего курса, а также по теории функций комплексного переменного и операционному исчислению.

 

С 1951 по 1978 годы на кафедре «Высшая математика» работала старший преподаватель Валентина Александровна Тарасова (1917-1987). Она вела занятия по всем разделам общего курса: математическому анализу, аналитической геометрии, дифференциальным уравнениям, кратным интегралам, теории функций комплексного переменного. Преподаватель и методист высокого уровня, В.А.Тарасова умела ясно и доступно объяснить самые сложные разделы курса.

 

Не одно десятилетие на кафедре плодотворно работали старшие преподаватели Клариса Григорьевна Лобова, Людмила Петровна Макарова, Нина Николаевна Бурмистрова. Учебной лабораторией кафедры руководила Нина Степановна Демешева.

                                       

 

В 1960-1965 гг. кафедрой высшей математики руководил доктор технических наук, профессор Николай Константинович Куликов (1917-1999).

 

Н.К.Куликов окончил МВТУ им. Н.Э.Баумана по специальности «Гусеничные машины». Кроме того, он учился заочно на механико–математическом факультете МГУ им. М.В.Ломоносова (в связи с началом Великой Отечественной войны окончил только два курса). После окончания МВТУ Н.К.Куликов работал инженером на Кировском заводе в Ленинграде, в Научно–исследовательском автомобильном и автомоторном институте, во ВНИИ Стройдормаш. С 1955 по 1960 годы заведовал кафедрой «Тракторостроение и двигатели внутреннего сгорания» Сталинградского механического института. В 1947 году Н.К.Куликов защитил кандидатскую диссертацию на тему «Теория клиновых механизмов свободного хода», а в 1952 году - докторскую диссертацию на тему «Теория динамики и экономики автомобиля в процессе разгона».

 

Научные интересы Н.К.Куликова были разнообразны: ему принадлежат работы, посвященные повышению экономических и динамических свойств автомобиля, расчету автомобильных и гидростатических передач, расчету одноступенчатого гидротрансформатора на режиме наибольшего коэффициента трансформации.

 

Поставленные технические задачи требовали применения сложного математического аппарата. Н.К.Куликов разрабатывал методы решения систем обыкновенных дифференциальных уравнений с переменными коэффициентами, описывающих сложные динамические устройства, в том числе системы автоматического регулирования. Ему принадлежат работы, посвященные свободным и вынужденным колебаниям нелинейных систем, нахождения периодического решения нелинейного дифференциального уравнения первого порядка, нахождения предела общего решения данного уравнения. Отметим также монографию Н.К.Куликова «Инженерный метод решения и исследования обыкновенных линейных дифференциальных уравнений», опубликованную в 1964 году.

 

Ряд работ Н.К.Куликова посвящен общим  принципам научной организации труда и применению их в учебном процессе и научно-исследовательской работе втуза, а также роли математики в формировании научного мировоззрения у студентов.

После ухода из МВТУ Н.К.Куликов заведовал кафедрой высшей математики в Пищевом институте,кафедрой «Системы управления» Академии МВД СССР, работал в Челябинском Политехническом институте, сотрудничал с Казахским государственным университетом.

 

В 1966-1969 гг. заведующим кафедрой был доктор физико - математических наук, профессор Ивлев Дюис Данилович (1930-2013). Его научные исследования посвящены механике деформируемого тела. Д.Д.Ивлев построил общую теорию идеальной пластичности с единым математическим аппаратом статически определимых уравнений гиперболического типа, соответствующим сдвиговой природе идеально пластического деформирования.

 

Д.Д.Ивлев исследовал разрывные решения пространственного состояния идеально пластических тел, получил решения различных задач о вдавливании штампов в идеально пластическое полупространство, о предельном состоянии материала, сжатого шероховатыми плитами. В его работах дальнейшее развитие получило изучение стационарных и нестационарных течений идеально пластических сред. Д.Д.Ивлев распространил представления ассоциированного закона течения на случай обобщенных переменных, определение соотношений в подобной форме позволило выделить члены, определяющие влияние анизотропии материала.

 

Значительное место в работах Д.Д.Ивлева уделено вопросам двойственности: эквивалентному построению теории пластичности на основе определения функции нагружения и ассоциированного закона пластического течения, либо определения диссипативной функции и ассоциированного закона нагружения. Им проанализированы различные постулаты, лежащие в основе построения теории пластичности, определена симметричная сводка интегральных неравенств, приводящих к ассоциированному закону пластического течения и ассоциированному закону нагружения.

 

В теории упрочняющихся пластических сред Д.Д.Ивлев развивал представления, основанные на трансляционном механизме упрочнения. Им предложен алгоритм построения моделей сложных сред, обладающих внутренними механизмами пластичности, вязкости, упругости.

 

Цикл работ Д.Д.Ивлева посвящен линеаризированным задачам упругопластического состояния тел. Метод малого параметра, развитый в работах Д.Д.Ивлева, позволил получить решение ряда плоских, осесимметричных, пространственных задач упругопластического состояния тел и определить неизвестную границу, отделяющую область пластического состояния материала, описываемую уравнениями гиперболического типа, от области упругого состояния тела, описываемой уравнениями эллиптического типа.

Ряд исследований Д.Д.Ивлева посвящен деформационной теории пластичности, вопросам построения моделей теории упругостии гидродинамики, предельному состоянию конструкций, статике и динамике сыпучих сред, механике квазихрупкого разрушения.

 

Работы Д.Д.Ивлева внесли фундаментальный вклад в механику деформируемого твёрдого тела. Он является автором более 300 научных трудов, среди которых монографии «Теория идеальной пластичности», «Теория уплотняющегося пластического тела», «Метод возмущений теории упруго-пластичного тела», 30 авторских свидетельств на изобретения. Под научным руководством Д.Д.Ивлева защищено более 70 кандидатских диссертаций. Среди его учеников доценты кафедры «Высшая математика» МВТУ им. Н.Э.Баумана В.В.Дуров и В.В.Кузнецов.

 

В 1970 году группа преподавателей кафедры «Высшая математика» бала награждена медалями «В ознаменование 100-летия со дня рождения Владимира Ильича Ленина».

 

 

---

 

Организация общетехнического факультета

 

В 1964 году в МВТУ был вновь образован общетехнический факультет. Он объединил кафедры высшей математики, физики, химии, теоретической механики, и другие (всего 11 кафедр). В связи с необходимостью конкретизировать учебно-методическую работу с учетом специальностей на кафедрах общетехнического факультета были организованы секции по факультетскому принципу. Каждый преподаватель работал только в одной секции и вел занятия только на одном выпускающем факультете.

 

Коллектив преподавателей общетехнического факультета принял участие в работе по теме «Научные основы учебного процесса». Исследования привели к выводу о том, что училище должно продолжать развивать традицию подготовки инженеров широкого профиля для отраслей машиностроения и приборостроения. Эти исследования позволили разработать рекомендации по усовершенствованию форм, методов и организации учебного процесса на младших курсах. На их базе были составлены и утверждены новые учебные планы.

 

В 1960-е годы кафедра пополнилась талантливыми исследователями и педагогами, среди которых доценты Н.Т.Вилисова, Л.Д.Покровский, Л.П.Паршев, В.В.Кузнецов, И.О.Янов, Я.Г.Ковалев, Г.И.Богомолов, В.Г.Крапоткин, В.В.Дуров, Р.С.Зотина, Г.С.Зайцева, Э.И.Агаева, А.Ф.Пелевина, В.С.Каменский, С.В.Синегуб, ассистенты О.А.Бархатова, И.В.Дубограй, А.Ф.Чудакова, И.Б.Клунникова, Э.П.Ганина, Т.И.Белова, Р.Ф.Сперанская, Е.В.Максимова, О.В.Роткова.

 

Профессор Богомолов Георгий Иванович (1922-2008), доктор технических наук, после окончания МАИ им. С.Орджоникидзе несколько лет работал в ЦНИИМАШ, а с 1961 по 1997 годы - на кафедре «Высшая математика» МГТУ им. Н.Э.Баумана. С 1997 года Г.И.Богомолов работал на кафедре «Вычислительная математика и математическая физика».

 

Научная деятельность Г.И.Богомолова посвящена исследованию аэродинамических форм гиперзвуковых летательных аппаратов. Ему принадлежат более шестидесяти научных работ и авторских свидетельств. Г.И.Богомолов был заместителем заведующего кафедрой по научной работе.

 

Г.И.Богомолов читал лекции как по общему курсу, так и ряд специальных курсов, таких как: численные методы анализа, уравнения математической физики, теория вероятностей и математическая статистика. Методы оптимизации, разработанные Г.И.Богомоловым, нашли свое отражение в курсе вариационного исчисления, который читался им на факультете повышения квалификации преподавателей. Г.И.Богомолов руководил научными студенческими кружками в области прикладной математики.

 

Г.И.Богомолов - участник боевых действий на Халхин-Голе в составе 289 мотострелкового полка. Награжден медалью «За победу над Японией», а также юбилейными медалями.

 

Более сорока лет работал на кафедре «Высшая математика» доцент Мирославлев Евгений Николаевич (1914-1990), кандидат физико-математических наук. Он был заместителем заведующего кафедрой, членом программно – методической комиссии министерства Высшего образования, заместителем председателя бюро секции ВТУЗов в математическом обществе.

 

Научные работы Е.Н.Мирославлева посвящены исследованию устойчивости нелинейных систем, периода колебания баланса. Кроме того, Е.Н.Мирославлев – автор ряда методических пособий по линейной алгебре, вариационному исчислению.

 

Е.Н.Мирославлев - участник Великой Отечественной войны. С августа 1941 года после окончания курсов радистов – разведчиков он находился в действующей армии. В декабре 1941 года принял участие в высадке десанта на Керчь и Феодосию, в 1942 году – в тяжелых оборонительных боях за Крым и Северный Кавказ. Затем в управлении контрразведки северной группы войск Кавказского фронта Е.Н.Мирославлев участвовал в подготовке радистов – разведчиков. После освобождения Крыма в 1944 году Е.Н.Мирославлев был направлен на третий прибалтийский фронт. Войну окончил в звании старшины. Награжден орденом «Красная звезда», медалями «За отвагу», «За оборону Кавказа», «За победу над Германией».

 

Доцент Дуров Виталий Васильевич (1938-2002), кандидат физико-математических наук, работал на кафедре «Высшая математика» с 1963 по 2002 годы. Был заместителем заведующего кафедрой по методической работе.

 

Научные труды В.В.Дурова посвящены изучению вдавливания твердых тел в пластическую среду, методов оценивания показателей надежности различных изделий, методов форсированных испытаний.

 

В.В.Дурову также принадлежит ряд методических пособий по математическому анализу, линейной алгебре, тензорному исчислению.

 

С 1966 по 1968 годы В.В.Дуров работал в Гвинее, в Педагогическом институте города Канкан. Читал лекции по математике на французском языке. А с 1974 по 1978 годы В.В.Дуров работал в Национальном институте нефти, газа и химии в Алжире, в городе Бумердесе.

 

Доцент Зотина Римма Сергеевна (1927-2011), кандидат физико-математических наук, работала на кафедре «Высшая математика» с 1961 по 1993 годы. В течение многих лет была заместителем заведующего кафедрой по методической работе, а в 1970 году исполняла обязанности заведующего кафедрой «Высшая математика».

 

Среди научных трудов Р.С.Зотиной – работы по истории развития математики в России. В своей диссертации на тему «Вопросы обоснования математического анализа в 18 и начале 19 века в России» Р.С.Зотина изучила деятельность Леонарда Эйлера как систематизатора огромного научного материала, накопленного Ньютоном, Лейбницем, братьями Бернулли, а также как создателя первой в России математической школы. Р.С.Зотина исследовала деятельность учеников Эйлера: Н.И.Фусса, С.К.Котельникова, а также математиков следующего поколения: С.Е.Гурьева, П.А.Рахманова, А.А.Барсова, выступавших за новые методологические установки в анализе бесконечно малых. Эти математики являлись проводниками и распространителями метода пределов, лежащего в основе строгого обоснования математического анализа.

 

Другим направлением научной деятельности Р.С.Зотиной были исследования развития, роста и старения организмов на базе термодинамики неравновесных процессов. В ряде статей рассмотрены системы дифференциальных уравнений биологии развития. Исследованы разные уровни аппроксимации, позволяющие получить уравнения, описывающие основные феноменологические явления, происходящие в онтогенезе животных и растений. Основные результаты данных исследований опубликованы в монографии: А.И.Зотин, Р.С.Зотина. «Феноменологическая теория развития, роста и старения организма».

 

Р.С.Зотина принимала активное участие в методической работе кафедры «Высшая математика». Ей принадлежит ряд методических пособий по векторной и линейной алгебре, теории вероятностей и математической стастике, теории функций комплексного переменного, линейному программированию.

 

Более двадцати лет на кафедре «Высшая математика» работал доцент Синегуб Сергей Владимирович (1913-1989), кандидат технических наук. В 1969 году он исполнял обязанности заведующего кафедрой.

 

В своих научных исследованиях С.В.Синегуб использовал операторный метод для решения проблем Майера и Лагранжа.

 

С 1965 по 1968 годы С.В.Синегуб работал в Алжире.

 

Доцент Савельев Сергей Иванович (1925-1983), кандидат физико-математических наук, работал на кафедре «Высшая математика» с 1957 по 1983 годы. Вел занятия по всем разделам общего курса, а также по уравнениям математической физики и по математической обработке результатов наблюдений. Был руководителем секции математики на факультете энергомашиностроения.

 

Научные труды С.И.Савельева посвящены методам нахождения приближенных решений дифференциальных уравнений второго порядка, а также исследованию динамики электропневматического клапана при закрывающем ходе мембраны. Кроме того, С.И.Савельев является автором нескольких методических пособий по уравнениям математической физики.

 

 

 

 

Доцент Ковалев Яков Григорьевич (1917-2004), кандидат физико-математических наук, работал на кафедре «Высшая математика» с 1955 по 1992 годы.

 

Научные интересы Я.Г.Ковалева лежали в области аэродинамики. В 1950 году он защитил кандидатскую диссертацию на тему «Применение вариационного метода к решению некоторых задач аэромеханики сжимаемого тела». Дальнейшие научные исследования Я.Г.Ковалева посвящены изучению демпфирующего момента крена крыла в сверхзвуковом потоке газа, расчету стационарного и нестационарного температурного поля в различных областях, численным методам решения уравнений в частных производных с помощью электроинтегратора.

 

Я.Г.Ковалев – участник Великой Отечественной войны. В сентябре 1941 года он был призван в Красную армию и направлен в военное училище, после окончания которого был назначен командиром стрелковой роты. В составе 1-го Украинского фронта участвовал в освобождении Праги. Награжден медалями «За освобождение Праги», «За победу над Германией».

 

Доцент Каменский Валентин Саввич, кандидат физико-математических наук, работал на кафедре «Высшая математика» более двадцати лет. Он является автором научных работ различной тематики: «Об одном частном случае решения задачи фильтрации сигналов», «О демпфировании вращательного движения твердого тела», «О задаче прогнозирования винеровского случайного процесса», «Об устойчивости демпфированного вращения твердого тела вокруг центра масс», «Об асимптотическом поведении решения нелинейной системы уравнений движения тела относительно неподвижной точки», «Об устойчивости движения в римановом пространстве».

 

Доцент Осипова Маргарита Зотовна (1925-2010), кандидат физико-математических наук, работала на кафедре «Высшая математика» с 1958 по 1982 годы.

 

М.З.Осипова является автором ряда научных работ по высшей геометрии и топологии, однако в первую очередь она известна как выдающийся методист. М.З.Осипова вела занятия по самым разным разделам курса высшей математики, работала со студентами всех факультетов, а также на вечернем и подготовительном отделениях. Особое внимание уделяла разработке вариантов типовых домашних заданий для студентов.

 

М.З.Осипова – автор методических пособий по числовым и функциональным рядам, теории поля, теории функций комплексного переменного, специальным функциям. Эти пособия написаны на высшем научно – методическом уровне и используются студентами МГТУ им. Н.Э.Баумана в течение нескольких десятилетий.

 

Более пятидесяти лет проработала в МВТУ – МГТУ им. Н.Э.Баумана доцент Щетинина Нина Николаевна (1923-2007), кандидат физико – математических наук. С 1950 по 1973 годы – на кафедре «Высшая математика», с 1973 по 1997 годы на кафедре «Прикладная математика», а с 1997 по 2002 годы – на кафедре «Математическое моделирование».

 

Научные исследования Н.Н.Щетининой посвящены вопросам механического поведения тел при интенсивном динамическом соударении (в частности, метеоритов), а также соударению и разлету частиц газа.

 

В течение многих лет Н.Н.Щетинина была заместителем заведующего кафедрой «Прикладная математика». Ей принадлежит ряд методических пособий по теории определителей и по приложениям дифференциального исчисления к исследованию функций.

 

 

Доцент Зайцева Галина Степановна, кандидат физико-математических наук, работала на кафедре «Высшая математика» с 1960 по 1995 годы. Была руководителем методического семинара кафедры, заведовала секцией.

 

Г.С.Зайцевой принадлежит ряд научных работ по теории дифференциальных уравнений. В частности, она получила новые оценки длины промежутка неосцилляции линейных дифференциальных операторов высших порядков путем некоторого обобщения классического метода Валле-Пуссена получения таких оценок. Кроме того, Г.С.Зайцева активно занималась научно-исследовательской работой совместно с различными кафедрами МВТУ: исследовала устойчивость суппортов металлорежущих станков, занималась оптимизацией наладки станков с ЧПУ, изучала оптимальные параметры поршневых компрессов общего назначения.

 

Также Г.С.Зайцева является автором ряда методических пособий по числовым и функциональным рядам.

 

Доцент Агаева Эльза Ибрагимовна (1932-1997), кандидат технических наук, работала на кафедре «Высшая математика» с 1967 по 1991 годы. Была заместителем заведующего кафедрой «Высшая математика» по методической работе.

 

После окончания механико-математического факультета МГУ им. М.В.Ломоносова Э.И.Агаева в течение нескольких лет работала в ЦИАМ им. П.И.Баранова, в научно – исследовательском секторе Московского Горного института. Проводила научные исследования в области газовой динамики, а также математического моделирования в горном деле.

 

Э.И.Агаевой принадлежит ряд методических пособий по аналитической геометрии, теории функций комплексной переменной.

 

Доцент Ершова Маргарита Игнатьевна (1930-2009), кандидат физико-математических наук, работала на кафедре «Высшая математика» с 1958 по 2000 годы. В течение нескольких лет руководила методическим семинаром кафедры «Высшая математика».

 

М.И.Ершовой принадлежит ряд научных работ и методических пособий по теории функций комплексного переменного и операционному исчислению.

 

М.И.Ершова увлекалась альпинизмом, туризмом, горными лыжами. Была организатором многих туристических и лыжных походов сотрудников кафедры. Вела фотолетопись жизни кафедры, была бессменным редактором стенгазеты кафедры.

 

Доцент Пелевина Алла Федоровна (1936-2013), кандидат физико-математических наук, работала на кафедре «Высшая математика» с 1968 по 1997 годы, а с 1997 по 2003 годы работала на кафедре «Вычислительная математика и математическая физика». Была профоргом кафедры.

 

Научные труды А.Ф.Пелевиной посвящены вопросам качественной теории дифференциальных уравнений и методам их решения: устойчивости решений дифференциальных уравнений с отклоняющимся аргументом, числам Рейнольдса и кривой Рейнольдса для уравнения Навье – Стокса, абсолютной устойчивости систем автоматического регулирования с запаздыванием, численным методам решения уравнения Пуассона.

 

А.Ф.Пелевина также является автором ряда методических пособий по аналитической геометрии и дифференциальным уравнениям.

 

Доцент Янов Игорь Олегович, кандидат технических наук, работал на кафедре «Высшая математика» с 1969 по 2012 годы. Заведовал вечерней секцией кафедры. Специалист в области исследования динамики систем ориентации самолетов и космических аппаратов с использованием солнечного давления, а также идентификации параметров водопроводных сетей. В течение долгого времени работал по совместительству на кафедре «Информационные системы и телекоммуникации» (ИУ-3) в должности старшего научного сотрудника. И.О.Янов - автор около пятидесяти научных работ и трех изобретений, а также методических пособий по линейной алгебре, дифференциальным уравнениям, кратным интегралам, числовым рядам, теории функций комплексного переменного.

 

Доцент Кузнецов Владимир Владимирович, кандидат физико – математических наук, работал на кафедре с 1966 по 2014 годы. Он участвовал в создании СУНЦ (физико-математический лицей №1580 при МГТУ им. Н. Э. Баумана), а также в течение восьми лет был его директором.

 

В.В.Кузнецов – заслуженный мастер спорта СССР, чемпион мира, призер Олимпийских игр по водному поло.

 

Научные труды В.В.Кузнецова посвящены исследованию упруго - пластических состояний толстой пластины, концентрации напряжений вблизи эллиптических отверстий под действием внутреннего давления.

 

В.В.Кузнецов является автором большого числа учебных пособий для студентов и школьников. Среди них сборники задач по аналитической геометрии и линейной алгебре, методические пособия по теории матриц, графикам элементарных функций, элементам теории множеств и математической логики, пособие по решению уравнений и неравенств для абитуриентов.

 

Старший преподаватель Бархатова Ольга Алексеевна (1940-2009) работала на кафедре «Высшая математика» с 1963 по 2009 годы. Ее научные труды посвящены разработке методов ускоренных испытаний изделий на безотказность и долговечность, проверке модели Седякина по результатам испытаний в случайном и переменном режимах.

 

В течение десяти лет О.А.Бархатова работала в предметной комиссии МГТУ им. Н.Э Баумана по приему вступительных экзаменов. Была членом совета по математической подготовке, координировала выпуск учебно-методической литературы по математике, была ученым секретарем кафедры «Высшая математика». Автор более двадцати научных и методических работ.

 

Старший преподаватель Клунникова Изабелла Борисовна работала на кафедре «Высшая математика» с 1964 по 1996 годы. Заведовала секцией МТ.

 

Научные труды И.Б.Клунниковой посвящены оценкам некоторых функционалов от случайных процессов, выбору весовых коэффициентов квадратичного функционала из заданных свойств динамической системы, методам оценки надежности изделий, выпускаемых мелкими партиями.

 

И.Б.Клунникова также является автором ряда методических пособий по числовым и степенным рядам.

 

Старший преподаватель Сперанская Римма Федоровна (1936-1996), работала на кафедре с 1963 по 1996 годы. Заведовала секцией К.

 

Р.Ф.Сперанская – автор ряда научных работ, посвященных методам форсированных испытаний технических изделий на ресурс, а также методических пособий по аналитической геометрии, линейной алгебре, степенным рядам.

 

Старший преподаватель Белова Тамара Ильинична (1941-2002) работала на кафедре «Высшая математика» с 1968 по 2002 годы. Была ученым секретарем кафедры, заведовала секцией МТ.

 

Т.И.Беловой принадлежит ряд научных работ, посвященных исследованию условий оптимальности в нелинейных системах автоматического регулирования, а также нескольких методических пособий по аналитической геометрии, интегральному исчислению, дифференциальным уравнениям.

 

Старший преподаватель Ганина Эльвира Петровна работала на кафедре «Высшая математика» с 1965 по 1998 годы. Вела занятия по всем разделам общего курса, а также по уравнениям математической физики. Была профоргом кафедры.

 

Э.П.Ганина – автор ряда методических пособий по математическому анализу и уравнениям математической физики.

 

Старший преподаватель Максимова Елена Владимировна работала на кафедре «Высшая математика» с 1965 по 1997 годы. С 1997 по 2002 годы работала на кафедре «Вычислительная математика и математическая физика».

 

Е.В.Максимова активно внедряла новые методы преподавания в учебный процесс, составляла карточки программированного контроля по различным разделам курса, разрабатывала плакаты и таблицы для кодоскопа. Участвовала в работе научного семинара «Теория поэтапного формирования умственных действий» в МГУ, сделала несколько докладов на конференции факультета «Новых методов обучения»  при Политехническом музее, на научно-методическом семинаре «Проблемы обучения в ВУЗе» в МВТУ.

 

Е.В.Максимова – автор ряда методических пособий по аналитической геометрии, числовым и степенным рядам.

Старший преподаватель Роткова Ольга Васильевна работала на кафедре «Высшая математика с 1965 по 1992 годы. Вела занятия по всем разделам общего курса.

 

Научные труды О.В.Ротковой посвящены особенностям и римановым поверхностям функций, определенных рядами Дирихле. Кроме того, О.В.Ротковой принадлежит ряд методических пособий по интегральному исчислению.

 

Старший преподаватель Чудакова Анна Филипповна работала на кафедре «Высшая математика» с 1964 по 1997 годы. С 1997 года работает на кафедре «Вычислительная математика и математическая физика». Была профоргом кафедры, заведовала секцией Э.

 

После окончания механико-математического факультета МГУ А.Ф.Чудакова работала на предприятии оборонной промышленности, где создавался зенитно-ракетный комплекс «Круг», в лаборатории, занимающейся проблемами флуктуации при наведении ракет на цель.

 

А.Ф.Чудакова является автором ряда научных статей в области теории управляющих систем, а также методических пособий по теории пределов, степенным рядам, дифференциальным уравнениям, теории вероятностей, теории функций комплексного переменного.

 

На протяжении многих лет А.Ф.Чудакова входила в состав предметной комиссии по приему вступительных экзаменов по математике.

 

Доцент Дубограй Ирина Валерьевна работала на кафедре «Высшая математика» с 1966 по 1997 годы. С 1997  года работает на кафедре «Вычислительная математика и математическая физика».

 

И.В.Дубограй является автором ряда научных статей в области теории управляющих систем, а также методических пособий по аналитической геометрии, линейной алгебре, дифференциальному и интегральному исчислению, дифференциальным уравнениям, теории поля, степенным рядам.

 

На протяжении многих лет И.В.Дубограй входила в состав предметной комиссии по приему вступительных экзаменов по математике.

 

И.В.Дубограй – кандидат в мастера спорта по художественной гимнастике.

 

Старший преподаватель Дьякова Людмила Николаевна работала на кафедре «Высшая математика» с 1972 по 1997 годы. С 1997 года работает на кафедре «Вычислительная математика и математическая физика». Была заместителем профорга, членом редколлегии кафедры «Высшая математика».

 

Л.Н.Дьякова является автором ряда научных статей в области теории управляющих систем, а также методических пособий по теории пределов, степенным рядам, дифференциальным уравнениям, теории вероятностей, теории функций комплексного переменного.

 

Старший преподаватель Тесалина Анастасия Андреевна работала на кафедре «Высшая математика» с 1961 по 1997 годы. С 1997 по 2001 годы работала на кафедре «Вычислительная математика и математическая физика». Вела занятия на ракетно – космическом факультете (Королев). Была ученым секретарем кафедры.

 

До прихода в МВТУ им. Н.Э. Баумана А.А. Тесалина работала в метеослужбе военной части. В 1965 - 1967 гг. вела занятия в Национальном институте нефти, газа и химии в Алжире, в городе Бумердесе.

 

А.А. Тесалина является автором методических пособий по аналитической геометрии и интегральному исчислению.

 

А.А. Тесалина увлекалась волейболом, горнолыжным спортом, туризмом, ходила в походы на байдарках.

 

Старший преподаватель Лунева Майя Степановна работала на кафедре «Высшая математика» с 1964 по 1989 годы. Вела занятия на ракетно – космическом факультете (Королев). Заведовала секцией РКТ. До прихода на кафедру работала на предприятии космической отрасли. Проводила исследования, посвященные посадке летательного аппарата на Луну.

 

М.С. Лунева является автором методических пособий по интегральному исчислению.

 

Старший преподаватель Киреева Юлия Григорьевна работала на кафедре «Высшая математика» с 1964 по 1989 годы. Вела занятия на ракетно – космическом факультете (Королев). До прихода на кафедру работала в ЦНИИМАШ, в лаборатории колебаний.

 

Ю.Г. Киреева участвовала в работе предметной комиссии по приему вступительных экзаменов по математике. Она является автором методических пособий по интегральному исчислению.

 

Ю.Г. Киреева – кандидат в мастера спорта по спортивной гимнастике. Она принимала участие в универсиадах.

 

Доцент Белова Людмила Дмитриевна, кандидат технических наук, работала в МГТУ им. Н.Э. Баумана с 1961 по 2012 годы.

 

Л.Д. Белова закончила МВТУ им. Н.Э. Баумана по специальности «Технология специального машиностроения». С 1961 по 1970 годы работала на кафедре М8, занималась оптимизацией технологических процессов.

 

С 1970 по 1997 годы Л.Д. Белова работала на кафедре «Высшая математика». Была членом культмассового сектора кафедры, организовывала посещения театров. Участвовала в работе предметной комиссии по приему вступительных экзаменов по математике.

 

С 1997 по 2012 годы Л.Д. Белова работала на кафедре «Вычислительная математика и математическая физика». В течение пяти лет была заместителем заведующего кафедрой по учебной работе.

 

Л.Д. Белова – автор методических пособий по линейной алгебре, кратным интегралам, теории функций комплексного переменного, линейному программированию. 

 

 

---

 

К началу 1970–х годов общее число преподавателей на кафедре было уже  около сотни, и встал вопрос о разделении кафедры. 12 июля 1971 года вышел приказ по Министерству высшего и среднего специального образования СССР об организации кафедры «Прикладная математика» в МВТУ им. Н.Э.Баумана. В соответствии с приказом по министерству ректор МВТУ Г.А.Николаев 19 февраля 1973 года издал приказ о разделении кафедры «Высшая математика» на две кафедры: «Высшая математика» и «Прикладная математика». Основу коллектива новой кафедры составили преподаватели секций машиностроительного и приборостроительного факультетов доценты С.В.Фролов, В.Ф.Панов, Ю.А.Почерников, О.И.Тескин, Н.Н.Щетинина, Э.П.Казанджан, Н.К.Брушлинский, В.Д.Морозова, Ю.И.Малов, В.Б.Чадов, И.Д.Фаликова, Е.В. Бекнева, ассистенты и старшие преподаватели С.М.Коган, К.Г.Лобова, Л.П.Макарова, Т.А.Хереско, Г.М.Цветкова, М.М.Сержантова, Г.П.Стась, З.Ф.Столярова, Г.С.Холмская, И.В.Шарохина, О.С. Петрухина.

 

В составе кафедры «Высшая математика» остались секции факультетов энергомашиностроения, механико-технологического и конструкторского.

 

Кафедру «Прикладная математика» возглавил лауреат Государственной премии СССР доктор технических наук, профессор Ростислав Сергеевич Судаков (1936-2012), создатель научной школы по теории испытаний систем. Р.С.Судаков – автор более 320 научных трудов, в том числе 25 монографий, среди которых «Основы теории надежности ракетных двигателей», «Статистические задачи отработки систем и таблицы для числовых расчетов показателей надежности», «Избыточность и объем испытаний технических систем и их элементов», «Теория псевдополуобратных матриц и ее применение в задачах надежности», «Испытания систем; выбор объемов и продолжительности», «Математические методы в прикладных задачах».

 

 

В 1985 – 2008 годах кафедрой «Прикладная математика» заведовал доктор технических наук, профессор Владимир Степанович Зарубин, специалист в области термомеханики материалов и теплонапряженных конструкций. Заслуженный деятель науки и техники Российской Федерации, академик Российской академии космонавтики. В.С.Зарубин внес существенный вклад в становление и развитие научного направления «Математическое моделирование термомеханических процессов в материалах и конструкциях». Он является автором  автор более 350 печатных работ, среди которых учебники и учебные пособия, десять монографий.

 

 

В.С. Зарубин является председателем секции термомеханики Совета по тепловым режимам машин и аппаратов РАН, членом Национального комитета РАН по тепломассообмену и Экспертного совета ВАК по авиационной и ракетно-космической технике, председателем диссертационного совета Д 053.15.12 по математическому моделированию, членом ещё четырех докторских диссертационных советов, входит в состав редколлегий журналов «Информационные технологии» и «Тепловые процессы в технике».

 

С 2008 года кафедрой «Прикладная математика» заведует доктор технических наук, профессор Кувыркин Георгий Николаевич, специалист в области математического моделирования термомеханических процессов в материалах и элементах конструкций. Ему принадлежат около 170 печатных работ, в том числе четыре монографии.

 

 

Г.Н.Кувыркин является членом Научного совета РАН по тепловым режимам машин и аппаратов, членом редколлегии журнала «Вестник МГТУ. Сер. Естественные науки», заместителем председателя диссертационного совета Д 212.141.15 по математическому моделированию.

 

Кафедру «Высшая математика» в 1973 году возглавил доктор физико - математических наук, профессор Михаил Сергеевич Яров-Яровой (1929–2004), известный математическими работами в области небесной механики, математики и численного интегрирования. Он разработал аналитическую теорию полетов космического корабля к Луне, выполнил исследование движения больших планет, провел численное интегрирование уравнений движений по уточненным формулам с использованием высших производных от решения, вывел новые представления потенциала небесных тел в эллипсоидальных координатах.

 

 

В 1976 году кафедру «Высшая математика» возглавил Геннадий Дмитриевич Карташов (1938–2008), заслуженный деятель науки Российской Федерации, крупный специалист в области ускоренных испытаний технических систем на надежность. Его кандидатская диссертация была посвящена решению проблемы восстановления многомерной функции распределения по ее известным маргинальным распределениям (если это возможно) или в оценке ее некоторых характеристик. В 1980 году Г.Д. Карташов защитил докторскую диссертацию «Исследование проблемы инвариантности в теории форсированных испытаний», в которой заложил основы теории ускоренных испытаний в нашей стране. Г.Д. Карташову удалось решить ряд сложных задач, возникающих в различных областях теории надёжности. В частности, им решена проблема планирования экспериментов с ненаблюдаемыми одновременно случайными величинами, проблема инвариантности в теории надёжности, установления области применимости различных моделей расходования ресурса изделий. На основе полученных теоретических результатов при помощи метода вложенных множеств Г.Д.Карташовым разработан новый подход к прогнозированию надежности изделий. В отличие от традиционного – аппроксимации реализаций изменения технических параметров по времени – предложена аппроксимация по ансамблю. Для последовательных систем, состоящих из большого количества разнотипных элементов, предложены приближенные асимптотические методы форсированных испытаний. Показано, в частности, что для дискретных систем асимптотически выполняется модель Пальмгрена-Майнера (линейного суммирования повреждений) и форсированные испытания таких систем можно проводить в рамках линейной модели, если отказы элементов полные. Г.Д.Карташов – автор более 250 работ, среди которых монографии: Г.Д.Карташов «Принципы расходования ресурса и их использование для оценки надежности» (1984); А.И.Перроте, Г.Д.Карташов, К.Н.Цветаев «Основы ускоренных испытаний радиоэлементов на надежность» (1968); Г.Д. Карташов «Ускоренные испытания элементов и систем» (1990), а также государственных стандартов.

 

 

 

Г.Д.Карташов уделял большое внимание научному росту сотрудников кафедры. Непосредственно под его руководством было подготовлено и защищено 18 кандидатских и 4 докторских диссертаций. А всего за более чем тридцатилетний период руководства Г.Д.Карташовым кафедрой «Высшая математика» ее преподавателями защищено более десяти докторских и несколько десятков кандидатских диссертаций.

 

 

В 1970-80-е годы кафедра «Высшая математика» пополнилась следующим поколением преподавателей, среди которых были профессора Е.М.Шахов, А.А.Грешилов, А.В.Печинкин, Г.С.Садыхов, доценты Л.П.Котельникова, С.К.Соболев, В.И.Тимонин, Л.Г.Ветров, В.Н.Белов, Л.Д. Белова, Н.И.Сидняев, В.Ю.Чуев, В.И.Леванков, В.И.Асатурян, П.Н.Антонюк, Б.Т.Добрица, К.В.Титов, В.Ф.Бережной, К.К.Василевский, Г.А.Кокотушкин, А.В.Копаев, В.Г.Богомолов, Л.М.Будовская, И.Г.Шведова, И.Г.Зорина, А.В.Неклюдов, В.В.Станцо, А.В.Филиновский, А.А.Федотов, П.В.Храпов, А.В.Мастихин, ассистенты и старшие преподаватели А.Г.Блюмин, Е.А.Воробьева, В.А.Ефрюшкина, Г.Н.Кошелева, Т.А.Цветкова.

 

 

Заместителями заведующего кафедрой были: по научной работе – доцент Лия Петровна Котельникова, по учебной работе – доцент Нина Трофимовна Вилисова, по методической работе – доцент Виталий Васильевич Дуров.

 

 

Среди основных научных направлений на кафедре были теория испытаний на надежность и использование физико-математических методов в технике. Кафедра осуществляла научное руководство семинаром по надежности в политехническом музее.

 

 

Основной формой методической работой были регулярные заседания научного семинара. На этих заседаниях рассматривались новые темы и программы курсов, новые методические пособия, новые методики изложения, а также изменения в школьной программе по математике. Все преподаватели кафедры должны были регулярно выступать на семинаре с докладом, причем на каждый доклад назначались по два оппонента, которые готовили письменные отзывы. Лучшие доклады рекомендовались к включению в сборник «Труды методического семинара кафедры высшей математики». Методическим семинаром кафедры руководила доцент Галина Степановна Зайцева.

 

 

С 1974 по 2002 годы учебной лабораторией кафедры руководила инженер Позднякова Татьяна Викторовна.

 

Доцент Котельникова Лия Петровна, кандидат технических наук, работала на кафедре «Высшая математика» с 1973 по 2001 годы, была заместителем заведующего кафедрой по научной работе.

 

 

После окончания МВТУ им. Н.Э.Баумана и механико-математического факультета МГУ им. М.В.Ломоносова Л.П.Котельникова работала на Уралмаше, затем в ВНИИМЕТМАШ. Она разработала новые технологические процессы прокатки колец, изготовления шланговых компенсаторов.

 

Научные труды Л.П.Котельниковой посвящены решению ряда практических задач, среди которых расчет цилиндрической оболочки, нагруженной внутренним давлением, расчет кабеля на прочность и надежность, оценка надежности изделий, выпускаемых мелкими партиями. Л.П.Котельникова – автор более двадцати научных работ и изобретений, большинство из которых внедрены.

 

Доцент Василевский Константин Константинович (1919-2006), кандидат физико-математических наук, работал на кафедре «Высшая математика» с 1971 по 1997 годы. С 1997 по 2002 годы работал на кафедре «Вычислительная математика и математическая физика». Читал лекции по всем разделам общего курса, а также специальный курс по уравнениям течения вязкого сжимаемого газа.

 

К.К.Василевский - автор около сорока научных работ, в которых использовал различные методы (метод функции Грина, операционный метод, метод разделения переменных) при решении уравнений параболического типа, возникающих в задачах теплофизики. Разрабатывал методики расчета тепловых нагрузок.

 

 

К.К.Василевский неоднократно выступал с докладами на различных научных конференциях, был членом секции Всесоюзного научного совета по проблемам массо – и теплопереноса в технологических процессах.

 

К.К.Василевский - участник Великой Отечественной войны. В июле – августе 1941 года в составе студенческого отряда МГУ он участвовал в сооружении противотанковых рвов под Смоленском, а уже в сентябре 1941 года был призван в Красную армию. Был командиром взвода, роты, военным переводчиком. С февраля 1945 года служил на первом Белорусском фронте. Участвовал в штурме Берлина. Войну закончил в звании старшего лейтенанта. Награжден медалями, среди которых «За взятие Берлина», «За победу над Германией».

 

С 1974 по 1998 годы на кафедре «Высшая математика» работал доцент Бережной Вячеслав Фирсович, кандидат технических наук. Автор более двадцати научных работ в области ускоренных испытаний технических систем.

 

 

В течение нескольких  лет В.Ф.Бережной входил в состав предметной комиссии по приему вступительных экзаменов по математике. Был секретарем партбюро кафедры.

 

В.Ф.Бережной активно использовал в учебном процессе вычислительную технику. Он является автором диалоговых обучающих программ, а также ряда методических пособий по численным методам математического анализа, линейной алгебры, уравнений математической физики.

 

В. Ф. Бережной – кандидат в мастера спорта по скоростному бегу на коньках. Был чемпионом Москвы среди юношей.

 

Доцент Чебурахин Игорь Федорович, кандидат технических наук, работал на  кафедре  «Высшая математика»МГТУ им. Н.Э.Баумана с 1971 по 1992 годы. Читал лекции по основным и специальным курсам высшей математики: «Дискретная математика», «Прикладное программирование», «Теория информации», «Теория конечных автоматов», «Схемотехника». Вел работу по созданию методического обеспечения и использованию ЭВМ в учебном процессе.

 

 

Областью научных интересов И. Ф. Чебурахина является теория и синтез дискретных управляющих систем: получение и анализ функционалов, характеризующих показатели качества представления булевых функций в различных базисах; точные верхние оценки сложности представления булевых функций в классе формул и классе схем из функциональных элементов. Ему принадлежит более 90 научных работ, среди которых отметим монографию «Синтез дискретных управляющих систем и математическое моделирование: теория, алгоритмы, программы», а также учебные пособия «Логическое управление: задачи, алгоритмы, показатели качества» и «Основные понятия теории конечных автоматов и некоторые ее приложения».

 

И. Ф. Чебурахин неоднократно принимал участие в работе различных симпозиумов, конференций, семинаров («Актуальные проблемы фундаментальных наук», «Интеллектуальные системы», «Дискретная математика и ее приложения», «Дискретные модели в теории управляющих систем», «Системы и комплексы автоматического управления в космонавтике и народном хозяйстве», «Проблемы теоретической кибернетики», Международный аэрокосмический конгресс).

 

С 2002 по 2014 годы И. Ф. Чебурахин заведовал кафедрой  «Кибернетика» МАТИ  им. К.Э.Циолковского. В 2004 году он защитил докторскую диссертацию и был утвержден в звании профессора.

 

Доцент Шведова Ирина Гавриловна, кандидат физико - математических наук, работала на кафедре «Высшая математика»МГТУ им. Н.Э.Баумана с 1977 по 1997 годы. С 1997 по 2003 годы работала на кафедре «Вычислительная математика и математическая физика». Была заместителем профорга кафедры.

 

 

И. Г. Шведова вела исследования в области ускоренных испытаний технических систем на надежность. В круг ее научных интересов входили оценки надежности по результатам приемо – сдаточных испытаний, оценки надежности изделий, эксплуатируемых в сложных режимах, решение экстремальных задач из теории управляемых марковских случайных процессов.

 

Под руководством Г. Д. Карташова И. Г. Шведова защитила кандидатскую диссертацию на тему «Приближенные методы оценивания некоторых функционалов от регрессии в задачах теории надежности».

 

И. Г. Шведова является автором ряда методических пособий по теории пределов, несобственным интегралам, интегралам, зависящим от параметра, а также пособия по геометрии для учителей.

 

В течение ряда лет на кафедре «Высшая математика» МГТУ им. Н. Э. Баумана работал по совместительству доцент Швартин Сергей Михайлович (1924 - 2009), кандидат физико-математических наук, инженер-исследователь Отдела математических проблем распознавания и методов комбинаторного анализа Вычислительного центра им. А. А. Дородницына РАН.

 

 

С. М. Швартин был специалистом в области планирования и оптимизации перевозок. Ему принадлежат важные результаты в теории транспортных задач линейного программирования.

 

С. М. Швартин – участник Великой Отечественной войны, награжден Орденом Красной звезды и медалями.

 

С 1987 по 2000 годы на кафедре «Высшая математика» работал профессор Печинкин Александр Владимирович (1946-2014), доктор физико – математических наук, признанный специалист в области разработки аналитических методов исследования систем массового обслуживания. Ему принадлежат более 200 научных работ в области теории вероятностей, математической статистики, теории массового обслуживания, моделирования информационно-вычислительных сетевых систем. Среди работ А.В.Печинкина 18 учебников, учебных пособий, монографий, в том числе изданных за рубежом. За создание серии учебников «Математика в техническом университете» А.В.Печинкин в составе коллектива авторов из МГТУ им. Н.Э.Баумана в 2004 году стал лауреатом премии Правительства РФ в области науки и техники.

 

 

А.В.Печинкин - участник большого числа Всесоюзных и Всероссийских и международных научных конференций. Был руководителем и исполнителем нескольких грантов РФФИ.

 

 

Профессор Садыхов Гулам Садыхович, доктор технических наук, работал на кафедре «Высшая математика» с 1991 по 2006 годы. С 2006 года работает на кафедре «Вычислительная математика и математическая физика».

 

После окончания Азербайджанского ГПИ и защиты кандидатской диссертации в Математическом институте им. В.А.Стеклова Г.С.Садыхов более 20 лет проработал на предприятиях радиоэлектронной промышленности, возглавляя отделы и лаборатории надежности. В 1989 году защитил докторскую диссертацию.

 

 

Г.С.Садыхов разработал фундаментальные научные основы оценок и контроля безопасности техногенно опасных объектов. Введенные показатели безопасности позволяют определять временные интервалы эксплуатации технических объектов с заданным уровнем безопасности, а также планировать испытания объектов на безопасность. Научные результаты Г.С.Садыхова в области оценок и контроля остаточного ресурса нашли широкое инженерное применение в задачах продления назначенного ресурса технических объектов. Определенные показатели ресурса «Средняя доля безотказной наработки», «Гамма-процентный остаточный ресурс» и др. вошли в государственные стандарты СССР и РФ.

 

Г.С.Садыхов - автор более 200 научных изданий и публикаций, среди которых монографии, справочники по надежности, государственные стандарты.

 

Г.С.Садыхов входит в состав диссертационного совета в ВЦ РАН РФ по специальности «Безопасность в чрезвычайных ситуациях», является членом редколлегии журнала «Методы менеджмента качества» Госстандарта России, членом Оргкомитета и руководителем секции «Реновация средств и объектов материального производства» ежегодного Международного симпозиума «Надежность и качество». Среди учеников Г.С.Садыхова 12 кандидатов и 2 доктора наук.

 

С 1994 по 2005 годы на кафедре «Высшая математика» работал профессор Баскаков Валерий Николаевич, доктор физико-математических наук, специалист в области актуарной математики. Автор более ста статей по пенсионному страхованию, восьми монографий, касающихся реформы пенсионных систем Российской Федерации и Республики Молдова и пяти учебных пособий по актуарной математике.

 

 

В. Н. Баскаков принимает активное участие в становлении российской пенсионной системы, входит в состав экспертных советов по вопросам негосударственного пенсионного обеспечения. Он является главным редактором журнала «Актуарий», членом редколлегии журнала «Пенсионные фонды и инвестиции».

 

Доцент Кокотушкин Георгий Александрович (1942-2014), кандидат физико – математических наук, работал на кафедре «Высшая математика» с 1988 по 2010 годы. Заведовал вычислительной секцией кафедры.

 

 

Основное направление научных исследований Г.А.Кокотушкина - численное решение дифференциальных уравнений в частных производных. Среди них - исследование внутреннего строения земной коры с помощью электромагнитных волн (поиск полезных ископаемых), задачи теплопроводности (в частности: распределение температуры и остывание доменных печей).

 

Г.А.Кокотушкин принимал активное участие в становлении курсов «Численные методы», «Вычислительная математика». Он подготовил несколько учебных пособий по данным курсам, разработал лабораторный практикум.

 

Старший преподаватель Блюмин Алексей Григорьевич (1951-2010)  работал на кафедре «Высшая математика» с 1978 по 2010 годы. Он вел занятия по всем разделам общего курса, а также по численным методам.

 

 

А.Г.Блюмин принимал активное участие в разработке лабораторного практикума, отладке и внедрению в учебный процесс обучающих программ на ЭВМ. Автор ряда методических пособий по численным методам.

 

 

 

 

Московский государственный технический университет имени Н.Э.Баумана

 

Начиная с 1989 года, наш вуз носит свое нынешнее название — Московский государственный технический университет (МГТУ) имени Н.Э.Баумана. В эти годы в стране происходили большие изменения, что, конечно, не могло не сказаться и на высшем образовании. Развивающиеся рыночные отношения требовали от вузов постоянного реагирования на их изменения. Рассматриваемый период времени совпал с интенсивным развитием информационных технологий и их внедрением во все сферы деятельности, в том числе в учебный процесс и научные исследования. Россия стала полноправным членом мирового сообщества, что вызвало активизацию международной деятельности вузов. Придание  многим техническим вузам статуса университета привело к улучшению фундаментальной, гуманитарной и экономической подготовки студентов. Эти и другие причины расширили сферы деятельности российских высших учебных заведений, в том числе МГТУ им. Н.Э. Баумана.

 

Становление и развитие нашего вуза как технического университета началось в очень сложное время. Распад Советского Союза в 1991 году, радикальное изменение политической ситуации и социально-экономических отношений привели к значительным трудностям в хозяйственной деятельности предприятий, краху многих из них, резкому снижению финансирования бюджетных организаций, в частности вузов.

 

Положение в МГТУ было настолько серьезным, что в начале 1990-х годов речь зачастую шла не о развитии образовательной деятельности, а о собственном выживании. Требовалось адаптироваться к изменившейся ситуации, сберечь научно-педагогические школы и кадровый состав.

 

Несмотря на все сложности, руководству кафедры «Высшая математика» удалось в целом сохранить коллектив. Более того, состав кафедры в 1990-е годы пополнился многими преподавателями высокой квалификации, среди которых были профессора И.В.Павлов, Р.С.Исмагилов, А.С.Савин, А.В.Калинкин, А.Т.Ильичев, Г.Г.Цыпкин, И.Б.Бахолдин, В.Ф.Кравченко, Э.Р.Смольяков, доценты Т.Е.Бояринцева, Л.Ю.Соломатина, В.Я.Томашпольский, А.В.Гласко, Д.А.Мельников, О.Н.Агеев, С.М.Акбаров, С.Б.Табалдыев, Л.Ю.Крыжановская, старшие преподаватели М.Н.Шевченко, Н.В.Золотова, Г.А.Шумова, Т.И.Лапшенкова, М.П.Григорьева.

 

В 1997 году было проведено еще одно разделение кафедры «Высшая математика». На ее базе была образована новая кафедра «Вычислительная математика и математическая физика», которую возглавил профессор Грешилов Анатолий Антонович, доктор технических наук, автор более 200 научных статей, 30 изобретений, более 30 монографий. Основные направления его научной деятельности - ядерная физика, конфлюэнтный анализ, некорректные задачи, математические методы принятия решений.

 

 

Основу коллектива новой кафедры составили преподаватели секции факультета энергомашиностроения кафедры «Высшая математика» профессора Г.И.Богомолов, А.И.Лошкарев, М.С.Яров-Яровой, доценты Б.Т.Добрица, М.В.Будилович, К.К.Василевский, Л.Д.Белова, В.Ю.Чуев, П.Н.Антонюк, К.В.Титов, А.Ф.Пелевина, старшие преподаватели И.В.Дубограй, Л.Н.Дьякова, А.Ф.Чудакова, Ю.В.Журавлев, Т.А.Цветкова.

 

В 2002 году заведующим кафедрой «Вычислительная математика и математическая физика» стал профессор Димитриенко Юрий Иванович, доктор физико-математических наук, крупный ученый в области механики сплошных сред, вычислительной механики и механики композитов, автор около 300 научных работ, в том числе 12 монографий и учебных пособий. С его приходом кафедра была полностью реформирована - в ее состав из кафедры «Прикладная математика» перешла большая секция на Аэрокосмическом факультете, в результате кафедра «Вычислительная математика и математическая физика» стала выпускающей: она стала готовить специалистов по направлению "Прикладная математика" на Аэрокосмическом факультете МГТУ им.Н.Э.Баумана.

 

 

Также в 1997 году было проведено разделение кафедры «Прикладная математика». На ее основе была образована новая кафедра «Математическое моделирование», которую возглавил профессор Крищенко Александр Петрович, доктор физико-математических наук, член-корреспондент РАН. Основные научные результаты А.П. Крищенко получены в области разработки методов анализа нелинейных систем и методов синтеза алгоритмов управления для нелинейных систем. Научные исследования, проводимые А.П. Крищенко, связаны с анализом аффинных систем, изучением их свойств управляемости, наблюдаемости, решением задач терминального управления в виде программных управлений и управлений в виде обратных связей, качественным анализом нелинейных систем.

 

 

Основу коллектива новой кафедры составили преподаватели секций факультетов ИУ и РЛ кафедры «Прикладная математика» профессора В.В.Феоктистов, И.К.Волков, доценты Ю.И.Малов, В.Б.Чадов, Н.Н.Щетинина, М.М. Сержантова, Т.А. Митюшкина, Т.В. Муратова, Е.Н. Жидков, старшие преподаватели И.В.Шарохина, И.Е.Кандаурова.

 

В 1999 году кафедра "Высшая математика" стала выпускающей. Она осуществляет подготовку инженеров-математиков по специальности "прикладная математика", специализирующихся в области стохастического анализа и моделей обработки информационных массивов.

 

Для студентов факультета ФН преподаватели кафедры разработали специальные курсы, некоторые из которых являются уникальными. Производственную практику студенты проходят на таких известных предприятиях, как научно-исследовательские институты ОАО «Газпром», «Росатом», Радиотехнический институт им. А.Л.Минца, «Центральный научно-исследовательский институт машиностроения».

 

В 2004 году вступил в строй учебно-лабораторный корпус МГТУ. Кафедра «Высшая математика» переехала в новое, более просторное помещение. В распоряжении кафедры две преподавательские, кабинет заведующего, две лаборатории, библиотека и аудитория для консультаций.

 

В 2008 году кафедру «Высшая математика» возглавил доктор технических наук, профессор Сидняев Николай Иванович.

 

---

 

Приложение

 

Программа курса математики ИМТУ 1892 года.

 

Курс 1 общего класса при 5 лекциях в неделю

 

А) Аналитическая геометрия на плоскости

 

Определение положения точки на оси. Правило знаков. Найти абсциссу точки, разделяющей расстояние между двумя данными точками в данном отношении. Проекция на ось. Величина и знак проекции прямой на данную ось. Проекция замыкающей стороны незамкнутого многоугольника. Сумма проекций сторон замкнутого многоугольника.

 

Проекция на плоскость. Теорема о площади проекции. Декартовы и полярные координаты на плоскости. Соотношение между прямоугольными и полярными координатами. Определение расстояния между двумя точками. Определение координат точки, разделяющей расстояние между двумя точками в данном отношении.

 

Декартовы и полярные координаты в пространстве. Соотношение между прямоугольными и полярными координатами. Определение расстояния между двумя точками. Определение координат точки, делящей расстояние между двумя точками в данном отношении.

 

Определение направления прямой. Найти косинусы углов, которые прямая, соединяющая две данные точки, образует с осями координат. Определить косинусы углов по их отношению. Определить косинусы углов радиуса вектора с осями по долготе и полярному углу. Определить косинусы угла между двумя прямыми. Соотношение между площадью данной фигуры и ее проекцией на плоскости координат.

 

Неравенства между сторонами и углами сферического треугольника. Вывод основной формулы сферического треугольника. Формула четырех синусов.

 

Формула косинуса угла сферического треугольника. Формула с котангенсами. Формулы прямоугольного сферического треугольника. Решение прямоугольных сферических треугольников.

 

Понятие о геометрическом месте и уравнении кривой. Уравнение в полярных координатах. Примеры.

 

Составление и исследование уравнения прямой. Уравнение круга и его вид в частных случаях.

 

Парабола как геометрическое место и ее построение. Составление уравнения параболы и исследование ее вида. Построение параболы, выводимое из ее уравнения.

 

Эллипс как геометрическое место и его построение непрерывным движением и по точкам. Составление уравнения эллипса и исследование его вида. Эксцентриситет и параметры эллипса. Построение эллипса, основанное на его уравнении. Эллипсограф.

 

Гипербола как геометрическое место и ее построение непрерывным движением и по точкам. Составление уравнения гиперболы и исследование ее вида. Асимптоты гиперболы, ее эксцентриситет и параметры. Построение гиперболы, выводимое из ее уравнения.

 

Конхоида и ее приложение к делению угла на три равные части. Циссоида и удвоение куба. Овал Кассини, лемниската.

 

Синусоида, кривая тангенсов, циклоида. Спирали: архимедова, логарифмическая и гиперболическая.

 

Формулы преобразования координат. Доказательство неизменности степени уравнения кривой с переменой координат.

 

Всякое уравнение прямой первой степени между двумя координатами представляет прямую. Различные формы уравнения прямой: по отрезку на оси координат и углу с осью абсцисс, по двум отрезкам, по данной точке и углу с осью абсцисс, по двум данным точкам, нормальная форма, полярное уравнение прямой.

 

Условие параллельности двух прямых. Составление уравнения кривой, проходящей через данную точку параллельно данной прямой. Координаты точки пересечения двух прямых.

 

Уравнение прямой, проходящей через точку пересечения двух данных прямых. Тангенс угла между двумя прямыми. Условие перпендикулярности двух прямых. Уравнение прямой, проходящей через данную точку перпендикулярно данной прямой. Длина перпендикуляра, опущенного из данной точки на прямую. Площадь треугольника по координатам его вершин.

 

Условие пересечения трех прямых в одной точке. Доказать, что перпендикуляры, опущенные из вершин треугольника на противоположные стороны, пересекаются в одной точке.

 

Условия, при котором три точки лежат на одной прямой. Доказать, что точки пересечения диагонали полного четырехугольника лежат на одной прямой.

 

Признак, при котором общее уравнение 2-ой степени представляет круг. Построение круга по данному уравнению. Полярное уравнение круга.

 

Уравнение касательной и нормали круга. Провести касательную параллельно данной прямой. Провести касательную к кругу из внешней точки. Радиальная ось двух кругов. Теорема о радиальных осях трех кругов.

 

Кривые второго порядка пересекают прямую в двух точках и не имеют точек перегиба. Построение прямой второго порядка с помощью решения ее уравнения в случае В²-4АС<0.

 

Построение прямой второго порядка с помощью решения ее уравнения в случае В²-4АС>0. Построение асимптот гиперболы.

 

Построение прямой второго порядка с помощью решения ее уравнения в случае В²-4АС=0.

 

Построение гиперболы в случае С=0. Построение параболы при В=0 и С=0.

 

Изыскание координат центра кривых 2-го порядка. Случаи, когда координаты центра бесконечны и не определены. Преобразование уравнения центральных кривых через перенесения начала координат в центр.

 

Изыскание направления главных осей центральных кривых второго порядка. Приведение уравнения центральной кривой к виду x²/a² ± y²/b²=1 .

 

Преобразование уравнения кривых, не имеющих центра: выбор направления оси абсцисс параллельно оси параболы, перенесение начала координат в вершину параболы.

 

Вывод уравнения эллипса из его свойств по отношению к фокусу и направляющей. Расстояние направляющей от центра, величина параметра. Выражение радиуса вектора в линейной функции абсциссы.

 

Вывод уравнения гиперболы из ее свойств по отношению к фокусу и направляющей. Расстояние направляющей от центра, величина параметра. Выражение радиуса вектора в линейной функции абсциссы. Вывод подобного выражения для параболы.

 

Полярное уравнение кривых второго порядка. Исследование формы.

 

Общее уравнение кривых второго порядка, отнесенных к вершине и фокальной оси. Парабола как предел эллипса и гиперболы.

 

О конических сечениях. Сечения цилиндра.

 

Общий вид уравнения касательных 2-го порядка. Уравнение поляры. Теоремы о полярах и полюсах.

 

Касательная к эллипсу. Углы, образуемые касательной с радиусами векторами. Произведение перпендикуляров, опущенных из фокусов на касательную. Геометрический способ проведения касательной через внешнюю точку. Место оснований перпендикуляров, опущенных из фокусов на касательную.

 

Касательная к гиперболе. Углы, образуемые касательной с радиусами векторами. Произведение перпендикуляров, опущенных из фокусов на касательную. Геометрический способ проведения касательных через внешнюю точку. Место оснований перпендикуляров, опущенных из фокусов на касательную.

 

Уравнение гиперболы, отнесенной к асимптотам. Площадь параллелограмма, построенного на координатах точки гиперболы. Доказать, что точка прикосновения разделяет отрезок касательной гиперболы между асимптотами пополам.

 

Касательная к параболе. Субтангенс и субнормаль. Угол касательной с радиусом вектором. Геометрический способ построения касательных из внешней точки.

 

Общий вид уравнения диаметров кривых второго порядка. В центральных кривых диаметры проходят через центр, а в параболе параллельны между собой. Сопряженные диаметры. Касательная в конце диаметра параллельна сопряженному диаметру. Вид уравнения параболы, отнесенной к диаметру и касательной, проходящей через его конец.

 

Сопряженные диаметры эллипса. Произведение тангенсов углов, образуемых сопряженными диаметрами с фокальной осью. Тангенс угла между двумя сопряженными диаметрами. Дополнительные хорды. Задача на дополнительные хорды.

 

Отнесение уравнения эллипса к сопряженным диаметрам. Длины сопряженных полудиаметров. Теоремы Апполония для эллипса.

 

Сопряженные диаметры гиперболы. Произведение тангенсов углов, образуемых сопряженными диаметрами с фокальной осью. Тангенс угла между сопряженными диаметрами. Доказать, что отрезки секущей между гиперболой и асимптотами равны между собой.

 

Отнесение уравнения гиперболы к сопряженным диаметрам. Величины действительного и мнимого полудиаметра. Показать, что параллелограмм, построенный на сопряженных диаметрах, имеет диагоналями асимптоты. Теоремы Апполония для гиперболы.

 

Уравнения диаметров параболы. Отнесение уравнения параболы к диаметру и касательной, проходящей через его конец. Геометрическое значение нового параметра в найденном уравнении.

 

 

Б) Начала высшей алгебры

 

Мнимые количества. Геометрическое и тригонометрическое представление их.

 

Сложение и вычитание.

 

Умножение и деление мнимых количеств. Возведение в степень и извлечение корня.

 

Решение двучленного уравнения вида: Xⁿ-1=0.

 

Решение двучленного уравнения вида: Xⁿ+1=0.

 

Решение уравнений третьей степени. Формула Кардано. Число корней. Случай равных корней.

 

Преобразование корней уравнения 3-ей степени в тригонометрическую форму в случае одного действительного корня.

 

Преобразование корней уравнения третьей степени в тригонометрическую форму в случае трех действительных корней.

 

Решение уравнений 4-ой степени по способу Декарта.

 

 

В) Дифференциальное исчисление

 

Процессы изменений. Величины постоянных и переменных.

 

Понятие о пределе. Основание способа пределов.

 

Понятие о бесконечном малом количестве. Отношение бесконечно малых.

 

Понятие о бесконечно большом количестве. Отношение бесконечно больших.

 

Понятие о функции. Функции явные и неявные. Классификация явных функций.

 

Понятие о непрерывном изменений независимого переменного и функция.

 

Геометрическое представление функции.

 

Основное свойство непрерывной однозначной функции.

 

Ряды сходящиеся и расходящиеся. Простейший признак сходимости ряда.

 

Наиболее общий признак сходимости ряда.

 

Теорема о перемножении рядов. Применение ее к биноминальному ряду.

 

Общие свойства биноминального ряда. Распространение формулы Ньютона.

 

Производная и ее геометрическое значение. Проведение касательной к данной кривой.

 

Производная степени с целым положительным показателем. Производная синуса.

 

Производная логарифма. О пределе: (1+1/m)^m. Несоизмеримость числа е. Неперовы логарифмы.

 

Производная алгебраической суммы. Производная постоянного. Производная произведения и частного.

 

Производная функции от функции.

 

Дифференцирование произвольной степени, логарифма и показательной функции.

 

Дифференцирование прямых круговых функций.

 

Дифференцирование обратных круговых функций.

 

Дифференцирование показательной функции с переменным основанием.

 

Дифференцирование выражений, содержащих функциональные знаки.

 

Производные высших порядков простейших функций.

 

Дифференцирование неявных функций. Дифференцирование системы уравнений, определяющих несколько неявных функций.

 

Признак непрерывности функции. Признак возрастания и убывания функции.

 

Теорема Ролля. Выражение приращения функции через среднее значение ее производной.

 

Следствие формулы, выражающей приращение функции через среднее значение ее производной.

 

Последовательный вывод формулы Тейлора с остатком Лагранжа.

 

Общий вывод формулы Тейлора с остатками Шлемильха, Лагранжа и Коши.

 

Ряд Маклорена. Разложение показательных и логарифмических функций. Преобразование логарифмических рядов.

 

Разложение синуса и косинуса. Мнимая показательная функция. Связь с тригонометрическими функциями. Периодичность мнимых показательных функций.

 

 

Курс 2 общего класса при 3 лекциях в неделю

 

А) Аналитическая геометрия в пространстве

 

Представление поверхности уравнением; примеры сферы и параболоида вращения.

 

Геометрическое значение уравнения с одного, двумя и тремя переменными; примеры.

 

Представление линии двумя уравнениями; примеры.

 

Геометрическое значение двух уравнений; примеры.

 

Уравнение плоскости.

 

Уравнение прямой.

 

Углы перпендикуляра к плоскости с осями координат.

 

Углы прямой с осями координат.

 

Уравнение прямой, проходящей через одну и две точки.

 

Уравнение прямой, проходящей через одну точку и имеющей данные углы с осями; уравнение прямой, проходящей через точку и параллельной данной прямой.

 

Пересечение прямых, плоскостей и прямой с плоскостью.

 

Уравнение плоскости, проходящей через одну точку и через три точки.

 

Уравнение параллельности плоскостей; уравнение плоскости, проходящей через точку, параллельно данной плоскости.

 

Уравнение плоскости, проходящей через линию и точку.

 

Условие перпендикулярности прямой и плоскости; уравнение прямой, проходящей через точку перпендикулярно данной плоскости.

 

Длина перпендикуляра из точки на линию.

 

Длина перпендикуляра из точки на плоскость.

 

Угол двух прямых.

 

Угол двух плоскостей.

 

Угол прямой с плоскостью.

 

Общее преобразование координат.

 

Преобразование Декартовых координат в Декартовы координаты.

 

Формулы Лагранжа.

 

Формулы Эйлера.

 

Классификация поверхностей.

 

Сферическая поверхность.

 

Общее уравнение цилиндров; примеры цилиндра косого с эллиптической направляющей и с направляющей кривой второго порядка.

 

Общее уравнение конусов; примеры кругового и эллиптического конусов.

 

Общее уравнение коноидов; примеры прямого коноида и коноидального клина.

 

Общее уравнение поверхности вращения около одной из осей координат; поверхность, получаемая от вращения прямой около оси.

 

Поверхности, получаемые от вращения кривых второго порядка.

 

Общее уравнение поверхности вращения около произвольной оси.

 

Теоремы о центре поверхности второго порядка.

 

Разыскание центра поверхности второго порядка.

 

Диаметральные плоскости поверхности второго порядка.

 

Разыскание главных диаметральных плоскостей поверхностей второго порядка.

 

Упрощение уравнения центральных поверхностей.

 

Упрощение уравнения поверхностей, не имеющих центра.

 

Трех-осный эллипсоид.

 

Однополостный гиперболоид.

 

Двуполостный гиперболоид.

 

Частные виды центральных поверхностей.

 

Эллиптический параболоид.

 

Гиперболический параболоид.

 

Построение образующих однополостного гиперболоида.

 

Построение образующих гиперболического параболоида.

 

Теоремы о свойствах образующих однополостного гиперболоида.

 

Теоремы о свойствах образующих гиперболического параболоида.

 

Образование однополостного гиперболоида движением прямой.

 

Образование гиперболического параболоида движением прямой.

 

 

Б) Высший анализ

 

Количества бесконечно малые. Разделение их на порядки. Отношение двух бесконечно малых. Произведение и сумма бесконечно малых.

 

Способ бесконечно малых. Два принципа способа бесконечно малых.

 

Понятие о дифференциале функции и его геометрическое значение. Правила дифференцирования явных функций одного независимого переменного. Производные высших порядков.

 

Различные случаи дифференцирования неявных функций одного независимого переменного. Производные высших порядков от неявных функций.

 

Дифференциал площади в прямоугольных и полярных координатах.

 

Предел отношения бесконечно малой дуги к хорде.

 

Дифференциал дуги плоской кривой в прямоугольных и полярных координатах.

 

О неопределенных видах 0/0 и "бесконечность"/"бесконечность" . Определение их истинных значений. Примеры.

 

Неопределенные виды "бескнечность"⁰, 1^{"бесконечность"}, 0⁰, "бесконечность"-"бесконечность". Замечание о неопределенных видах в неявных функциях. Примеры.

 

Наибольшие и наименьшие значения функции. Определение их и различение. Примеры.

 

Наибольшие и наименьшие значения неявных функций. Примеры.

 

Признаки наибольших и наименьших значений, выводимые из рассмотрения первой производной. Примеры.

 

О неопределенном интеграле. Доказательства его существования и его общее выражение. Основные формулы для интегрирования. Замечания для некоторых из них.

 

Интегрирование непосредственное. Приведение данных интегралов к основным формулам. Интеграл суммы. Интегрирование через разложение. Примеры.

 

Интегрирование по частям. Интегрирование через введение нового переменного. Примеры.

 

Интеграл как предел суммы. Пример непосредственного вычисления такого предела. Интеграл однопредельный. Интеграл определенный.

 

Касательные и нормали к плоским кривым. Касательная к трохоиде. Касательная к цепной линии.

 

Касательная к эпициклоидам и гипоциклоидам.

 

О выпуклости и вогнутости плоских кривых. Применение к эллипсу.

 

Разыскание точек перегиба. Примеры.

 

О кривизне плоских кривых. Радиус круга кривизны и центр его.

 

Выражение радиуса кривизны в Декартовых координатах. Применение к коническому сечению и к цепной линии.

 

О развертках. Общие свойства их. Радиус кривизны и развертка циклоида.

 

Составление уравнения развертки. Радиус кривизны и развертка параболы.

 

Радиус кривизны и развертка эллипса.

 

Касательные к кривым в полярных координатах. Спираль Архимеда.

 

Спирали гиперболическая и логарифмическая.

 

Радиус кривизны в полярных координатах. Кардиоида и развертывающая круга. Проведение к ним касательных.

 

Квадратура в Декартовых координатах. Определение замкнутой площади. Квадратура параболы и круга.

 

Квадратура в полярных координатах. Квадратура лемнискаты и Декартова листа.

 

Формула Симпсона. Геометрическое значение ее.

 

Ректификация в Декартовых координатах. Длина циклоиды.

 

Ректификация параболы.

 

Ректификация эллипса.

 

Ректификация в полярных координатах. Длина кардиоиды.

 

Дифференциал объема. Объемы, определяемые одним интегрированием. Объем отрезков эллипсоида и параболоида.

 

Объемы тел вращения. Объем от вращения циклоиды. Объем тора.

 

Дифференциал поверхности вращения. Поверхность шарового пояса. Поверхность удлиненного эллипсоида вращения.

 

Поверхность сжатого эллипсоида вращения.

 

 

Курс 3 общего класса механического отделения при 2 лекциях в неделю

 

А) Дифференциальное исчисление функций нескольких переменных

 

Дифференцирование сложной функции нескольких аргументов, зависящих от одного независимого переменного.

 

Независимость результата дифференцирования по нескольким аргументам от порядка дифференцирования.

 

Производные высших порядков сложных функций.

 

Производные неявных функций одного независимого переменного.

 

Дифференцирование функции нескольких независимых переменных. Теорема о дифференциале постоянного выражения.

 

Дифференцирование сложных функций нескольких переменных.

 

Дифференцирование неявных функций нескольких переменных.

 

Отдельное вычисление частных производных неявных функций.

 

Теорема Тейлора для функции многих переменных.

 

Наибольшие и наименьшие значения функций многих переменных.

 

Касательная линия и нормальная плоскость к кривым двоякой кривизны.

 

Касательная плоскость и нормальная линия к поверхностям.

 

Соприкасающаяся плоскость.

 

Главная нормаль.

 

Радиус первой кривизны и его различные выражения.

 

Тождество соприкасающегося круга с кругом кривизны.

 

Радиус второй кривизны.

 

Применение всех формул к винтовой линии.

 

 

Б) Высшая алгебра

 

Основные теоремы об изменении целой функции.

 

Теорема Коши о существовании корня.

 

Разложение функции на линейных множителей в случае однократных корней. Соотношение коэффициентов и корней.

 

Теорема о сопряженности мнимых корней.

 

Разложение функции на множителей второй степени в случае мнимых корней.

 

Теоретическое основание процесса выделения кратных корней.

 

Практическое выполнение процесса кратных корней.

 

Простейшие теоремы о числе действительных корней между данными пределами.

 

Теорема Декарта о числе положительных корней.

 

Теоремы о соизмеримых корнях. Выделение соизмеримых корней.

 

Теорема Штурма.

 

Отделение несоизмеримых корней по теореме Штурма. Первое вычисление корней по способу Лагранжа.

 

Вычисление корней по способу Ньютона и Фурье и по способу пропорциональных частей.

 

 

В) Интегральное исчисление

 

О неопределенном интеграле. Доказательство его существования и его общее выражение. Основные формы интегрирования. Замечания о некоторых из них.

 

Интегрирование непосредственное. Приведение данных интегралов к основным формулам. Интеграл суммы. Интегрирование через разложение. Примеры.

 

Интегрирование по частям. Интегрирование через введение нового переменного. Примеры.

 

Об интеграле определенном. Доказательство его существования. Площадь кривой линии. Способ для нахождения величины определенного интеграла. Интеграл исчезающий. Введение нового переменного в определенном интеграле.

 

Теоремы об определенном интеграле. Сравнение величин двух определенных интегралов. Замечание об интеграле с бесконечными пределами и об интеграле, в котором подынтегральная функция обращается в бесконечность при одном из пределов или между пределами интегрирования.

 

Вывод теоремы Тейлора с выражением остатка через определенный интеграл. Формула Лагранжа.

 

Интегрирование рациональных дробей. Случаи простых и действительных корней знаменателя. Примеры.

 

Интегрирование рациональных дробей в случае простых мнимых корней знаменателя. Примеры.

 

Разложение рациональных дробей в случае кратных действительных дробей знаменателя. Примеры интегрирования дроби для этого случая.

 

Разложение и интегрирование рациональной дроби в случае мнимых кратных корней знаменателя. Примеры интегрирования.

 

Интегралы, содержащие иррациональные одночлены, и другие интегралы, приводимые к этому виду. Примеры.

 

Интегралы, содержащие квадратный корень из функций 2-ой степени. Три преобразования. Интегралы, содержащие два корня из функции 1-ой степени.

 

Условия интегрируемости дифференциальных биномов. Примеры интегрирования. Замечания об эллиптических интегралах и функциях. Лежандровы интегралы.

 

Интегрирование логарифмических и показательных функций. Примеры.

 

Интегрирование круговых функций. Общий прием для вычисления интегралов с тригонометрическими функциями. Примеры.

 

Интегралы простых видов от тригонометрической функции. Интегралы от целых степеней синуса и косинуса.

 

Интегралы от степеней тангенса и котангенса и от произведения степеней синуса и косинуса. Вычисление интегралов от иррациональных функций через приведение их к тригонометрическим.

 

Определенный интеграл от степени синуса. Валлисово выражение π.

 

Об интегрировании помощью рядов. Разложение в ряд эллиптического интеграла 1-го рода.

 

О разложении функций в ряды помощью интегрирования. Вычисление арксинуса и арктангенса. Вычисление π.

 

Дифференцирование и интегрирование определенных интегралов по параметрам.

 

Выражение некоторых определенных интегралов, получаемых через дифференцирование и интегрирование известных выражений других определенных интегралов. Функция Гамма.

 

О двойных определенных интегралах. Двойной интеграл как предел суммы бесконечно малых. Геометрическое представление значений, получаемых переменными в двойном интеграле. Интегрирование по данной площади.

 

О тройных интегралах. Общая формула кубатур в двойных и тройных интегралах. Общая формула компланаций. Задачи на вычисление части поверхности сферы.

 

Понятие о дифференциальном уравнении. Существование общего интеграла для дифференциального уравнения 1-го порядка. Происхождение дифференциального уравнения из общего интеграла.

 

Отделение переменных. Однородные дифференциальные уравнения и приводимые к однородным. Линейные уравнения первого порядка. Уравнение Бернулли.

 

Полные дифференциальные уравнения. Примеры.

 

Об интегральном факторе, существование факторов.

 

Интегрирование дифференциальных уравнений первого порядка, но высших степеней. Интегрируемые формы.

 

Уравнение Клеро, его общее решение; геометрическое значение особого решения. Геометрическая задача, приводимая к уравнению Клеро.

 

Существование общего интеграла дифференциального уравнения n-го порядка. Происхождение такого уравнения.

 

Общий интеграл дифференциального линейного уравнения n-го порядка без известного члена. Уравнение с постоянными коэффициентами. Его интегрирование в разных случаях.

 

Интегрирование линейного уравнения с известным членом по способу изменения произвольных постоянных. Случай уравнения с постоянными коэффициентами. Интегрирование его, когда известно одно частное его решение.

 

Подробности

Категория: Общее

Опубликовано: 15 октября 2012

• Гранты для молодых ученых
• Поддержка ведущих научных школ
• Конкурсы РФФИ

 

Подробности

Категория: Общее

Опубликовано: 02 апреля 2012

История кафедры ФН-1

«Математика – наука о количественных отношениях и
пространственных формах действительного мира»

Кафедре «Высшая математика» Московского государствен­ного технического университета им. Н.Э. Баумана свыше – 140 лет.
Именно возраст заставил нас обратиться к истории кафедры, коллектив которого вписал не одну замечательную страницу в становление славы нашего университета.
Профессорско-преподавательский коллектив кафедры принимал самое активное участие в формировании базового образования, глубокой общенаучной и общеинженерной подготовки специалиста широкого профиля, способного работать не только по своей узкой специальности, но и в смежных областях науки и техники. И мы гордимся тем, что в достижения выпускников нашего вуза вложен и наш труд. Труд педагогического коллектива, усилиями которого успешно решается главная задача университета — обеспечение студентов современными знаниями в области математики. За время своего существования наш вуз выпустил, по самым скромным подсчетам, более 150 тысяч инженеров. И в успехах каждого из них есть вклад преподавателей кафедр, составляющих факультет «Фундаментальные науки» сегодня.
За время существования кафедры сменилось не одно поколение педагогов. Мы помним наших учителей – ученых и педагогов, усилиями которых была сформирована педагогическая школа воспитания инженеров, названная «русской». Конечно, упомянуть всех их в этом издании не представляется возможным, но мы испытываем чувство огромной благодарности ко всем, кто своим самоотверженным трудом ученого, педагога, воспитателя выковал целую плеяду инженерных кадров нашей Родины.
Предлагаемое вниманию читателя издание представляет собой коллективный труд. В подготовке материалов для него, уточнении содержания и редактировании участвовали несколько человек. Активное участие принимали в сборе материалов и сотрудники музея МГТУ им. Н.Э. Баумана.
Мы надеемся, что данное издание станет еще одним свидетельством славных традиций МГТУ им. Н.Э. Баумана, воспитанных многими поколениями ученых, педагогов, выпускников.

 

---

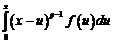
напечатанной в «Математическом сборнике» (т. 7, 1874 г.). При помощи предложенной им теории дифференцирования с дробным показателем ему удалось создать новый метод анализа особенностей решений обыкновенного дифференциального уравнения

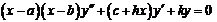
которое обобщает важные классы дифференциальных уравнений: гипергеометрическое, Бесселя, уравнения многочленов Лежандра и Чебышева. В 1882-1885 гг. в тт. 10-12 «Математического сборника» он опубликовал статьи о модификации этого метода применительно к сферическим функ­циям. Научные труды А.В.Летникова заслужили всеобщее признание, что было подтверждено избранием его членом-корреспондентом Петербургской академии наук.
Идеи А.В.Летникова в работах этого цикла непосредственно перекликались с идеями магистерской диссертации М.Е.Ващенко-Захарченко «Символическое исчисление и приложение его к интегрированию линейных дифференциальных уравнений» (1862 г., Киев) об упрощении решения дифференциальных и разностных уравнений. Серия работ английского ученого О.Хевисайда по применению операционного исчисления к решению электротехнических задач была начата лишь в 1887 г., причем в этих работах использовались подходы, сходные с идеями М.Е.Ващенко-Захарченко и А.В.Летникова, но без достаточно строгого математического обоснования. Научная работа А.В.Летникова была тесно связана с его педагогической деятельностью, что сыграло важную роль в математической подготовке инженеров в училище. Сложился характерный для А.В.Летникова стиль чтения лекций: простота, ясность при одновременной оригинальности математических доказательств.
Программа курса математики для различных отделений училища в то время включала аналитическую геометрию, анализ, сферическую геометрию, начала дифференциальной геометрии и высшей алгебры. Из специальных курсов выделялся прочитанный А.В.Летниковым курс вариационного исчисления, позднее вышедший отдельным изданием. Он был автором руководств по общим разделам анализа — дифференциальному и интегральному исчислению и их приложениям, дифференциальным уравнениям.
А.В.Летников помимо кафедры высшей математики возглавлял в учи­лище и комиссию по разработке общей системы теоретической и практи­ческой подготовки инженеров, получившей всемирную известность как «русский метод обучения ремеслам», преподавал математику в Межевом институте, а с 1883 г. был директором Московского коммерческого училища. Будучи одним из инициаторов создания и учредителей Московского математического общества, ученый сделал на его заседаниях 15 докладов, материалы которых печатались в выпускаемом этим обществом «Матема­тическом сборнике». В частности, в т. 3 этого сборника (1868) он впервые опубликовал на русском языке в своем переводе с немецкого одну из определяющих работ Н.И.Лобачевского «Геометрические основания теории параллельных». В предисловии к этой публикации А.В.Летников по достоинству оценил революционный переворот в геометрии, осуществленный Н.И.Лобачевским, и в дальнейшем в числе немногих русских математиков настойчиво пропагандировал его идеи. По инициативе А.В.Летникова в «Математическом сборнике» был создан специальный раздел по вопросам методики преподавания математики, причем не только высшей, но и элементарной. В этом разделе он напечатал несколько статей методического характера. Этим же вопросам была посвящена его речь «О системах реального образования», произнесенная им в ИМТУ в 1871 г. во время ежегодной торжественной церемонии выпуска студентов.
 

С 1872 г. начал свою работу в училище в должности преподавателя математики выдающийся русский ученый-механик, создатель кафедры теоретической механики в ИМТУ Николай Егорович Жуковский (1847-1921), который своими математическими исследованиями оказал влияние на развитие научной школы математики, в том числе в области качественной теории дифференциальных уравнений.
В своей магистерской диссертации «Кинематика жидкого тела», опубликованной в т. 8 «Математического сборника» (1876), при рассмотрении некоторых случаев плоскопараллельного движения несжимаемой жидкости он ввел классификацию особых точек дифференциальных уравнений первого порядка, которая содержала все четыре основных вида особых точек («узел», «седло», «фокус», «центр»), систематизированных затем в работах одного из признанных создателей качественной теории дифференциальных уравнений французского математика А.Пуанкаре.
Н.Е.Жуковский также исследовал поведение интегральных кривых в окрестности особой точки каждого вида. Однако это направление исследо­ваний, являвшееся лишь ответвлением его работ по механике, в дальнейшем не получило продолжения. Но авторитет Н.Е.Жуковского в развитии качественной теории дифференциальных уравнений был настолько высок, что в 1892 г. он выступил в Московском университете оппонентом на защите А.М.Ляпуновым докторской диссертации «Общая задача об устойчивости движения», в значительной мере определившей основные идеи и методы последующих работ в этой области.
Глубокая и взаимно обогащающая связь научных исследований по математике и механике, ярко проявившаяся в работах Н.Е.Жуковского, была характерна для научных школ этих направлений. Например, решение им задачи определения гидродинамических сил, в том числе подъемной силы при обтекании крыла воздушным потоком, в значительной мере повлияло на развитие разделов теории функций комплексного переменного, связанных с методами конформных отображений. Следует отметить, что за работу «О прочности движения» Н.Е.Жуковский в 1882 г. получил ученую степень доктора прикладной математики. Признанием авторитета Н.Е.Жуковского в области математики явилось избрание его в 1905 г. президентом Московского математического общества, постоянным членом которого он состоял с 1876 г.
 

Преподававший в ИМТУ в 1896-1906 гг. на кафедре теоретической механики его ученик, один из основоположников современной гидроаэродинамики, академик Сергей Алексеевич Чаплыгин (1869-1942) разработал приближенный метод интегрирования обыкновенных дифференциальных уравнений первого порядка и их систем, вошедший затем в математическую литературу под названием метода Чаплыгина.
В 1896 году начал свою работу на кафедре Евгений Александрович Болотов (1870-1922), известный математик и механик, выпускник Казанского университета. Его научные исследования относятся главным образом к аналитической механике. В 1907 г. Е.А. Болотов был утвержден в степени магистра прикладной математики за работу на тему «О движении материальной плоской фигуры, стесненной связями с трением». В своем отзыве на эту работу Н.Е. Жуковский отметил, что главная заслуга Болотова в этой работе – его геометрический анализ.

Самой значительной работой Болотова по аналитической механике является его исследование наиболее общего вариационного принципа механики – принципа наименьшего принуждения Гаусса. Е.А. Болотову принадлежит обобщение принципа наименьшего принуждения, которое легло в основу дальнейших исследований этого принципа учеными казанской школы механики. Представляют также интерес работы Болотова по гидромеханике и учебные руководства по курсам математического анализа и аналитической геометрии, которые ученый много лет читал в Московском техническом училище. В училище он читал курс аналитической геометрии и одновременно вел упражнения по теоретической и аналитической механике, которую читал Н.Е. Жуковский.
В лекциях по аналитической геометрии Болотов излагал аналитическую геометрию на плоскости и в пространстве, а также сферическую тригонометрию, увязывая многие разделы этого курса с отдельными вопросами теоретической механики и астрономии.
Е.А. Болотов уделял большое внимание подготовке своих лекций. Он обрабатывал их настолько детально и тщательно, что при издании их почти не требовалось редактировать.
С 1914 по 1921 гг. Е.А. Болотов заведовал кафедрой теоретической механики Казанского университета, а в 1921-1922 – кафедрой теоретической механики ИМТУ.

На формирование научной школы математики в училище не могла не оказать влияния деятельность выдающегося русского математика и механика академика Пафнутия Львовича Чебышева (1821-1894), у которого с преподавателями училища были давние дружеские отношения, несмотря на то, что научная жизнь ученого была связана главным образом с Санкт-Петербургом. В отчете училища за 1871 г. впервые была опубликована его работа «О центробежном уравнителе», которая явилась первым фундаментальным исследованием по теории регуляторов. В статье «О зубчатых колесах», напечатанной в 1872 г. в сборнике «Отчет и речи, произнесенные в торжественном собрании Императорского Московского технического училища 22 сентября 1872 года», он изложил аналитический метод расчета зубчатого зацепления.
В последующие годы П.Л.Чебышев регулярно посещал училище, чтобы руководить изготовлением и испытаниями в механической лаборатории спроектированных им регуляторов и других механизмов и устройств. Стремление усовершенствовать шарнирный механизм, называемый параллелограммом Уатта, натолкнуло его на постановку проблемы наилучшего приближения функций, заложившей основы глубокой математической теории, значение которой оказалось существенно шире первоначальной прикладной задачи. Ему принадлежит полушутливое высказывание о взаимосвязи теории и практики: «Математика пережила ранее два периода. В первом задачи ставились богами (делосская задача об удвоении куба), во втором — полубогами (Б.Паскаль, П.Ферма). Мы вошли теперь в третий период — задачи ставит нужда (практика), причем чем задача труднее, тем плодотворнее должны быть математические методы ее решения и тем шире область их последующего применения».

Отмеченная связь математических исследований с работами по механике и их определенная прикладная направленность прослеживаются и на последующих этапах развития научной школы математики. В 1936-1941 гг. кафедрой высшей математики заведовал д-р техн. наук, проф. Дмитрий Юрьевич Панов (1904–1975), специалист в области вычислительной математики, известный своими трудами по численному решению дифференциальных уравнений в частных производных, по нелинейной теории упругости и вибрации непризматических стержней сложного профиля.

 

Исследования в этих направлениях применительно к расчету воздушных винтов самолетов развивали в тесном контакте с ЦАГИ сотрудники кафедры Б.П. Демидович, П.М.Риз, Б.О. Солоноуц, А.Р. Янпольский.

 

 

 

С 1936 по 1948 гг. на кафедре работал доцент (в последствие профессор) Борис Павлович Демидович (1906-1977). Основными направлениями его научной деятельности были качественная теория обыкновенных дифференциальных уравнений, математическая физика и теория функций. В своих работах (их у него около шестидесяти) Б.П. Демидович исследовал динамические системы с интегральными инвариантами, периодические и почти периодические решения, ограниченные решения обыкновенных дифференциальных уравнений, правильные и вполне правильные дифференциальные системы, устойчивость обыкновенных дифференциальных уравнений, в частности, орбитальная устойчивость динамических систем.

С 1946 по 1961 гг. на кафедре работал д.ф.-м.н., профессор Петр Михайлович Риз (1902-1990). Он занимался такими проблемами как вопросы прочности в самолетостроении, теория случайных процессов, фундаментальные проблемы теории упругости. Его работы по математике и механике всегда отличались исключительной ясностью, глубиной исследований и одновременно краткостью изложения. П.М. Риз долгое время читал лекции для аспирантов и сотрудников института по совершенно различным разделам математики и механики, как, например, «Теория случайных процессов», «Теория нелинейных колебаний», «Исследование операций», «Методы функций в гидро- и аэродинамике».

 

В 1953-1958 гг. кафедру возглавлял д-р техн. наук, проф. Кирилл Петрович Станюкович (1916-1989), выдающийся физик-теоретик, астроном, газодинамик, заслуженный деятель науки и техники РСФСР. Всего им опубликовано более 600 научных работ. Он занимался проблемами метеорной астрономии, кратерообразования на Луне и планетах, вопросами гравитации, космогонии и космологии. В области газовой динамики изучал неустановившиеся движения сплошной среды, взрывные явления, проблемы космической газодинамики. В области теоретической физики – теорию гравитации и элементарных частиц. Его работы сыграли заметную роль в развитии ряда научных направлений в газовой динамике, теории детонации, релятивистской механике сплошной среды.
В 1959 г. кафедрой заведовал д-р техн. наук, проф. И.А.Паничкин, научные работы которого были посвящены вопросам обтекания тел вращения высокоскоростным воздушным потоком. Руководивший кафедрой в 1960-1965 гг. д-р техн. наук, проф. Н.К.Куликов разрабатывал методы решения систем обыкновенных дифференциальных уравнений с переменными коэффициентами, описывающих сложные динамические устройства, в том числе системы автоматического регулирования.
В 1966-1970 гг. заведующим кафедрой был д-р физ.-мат. наук, проф. Дюис Данилович Ивлев, известный своими работами по математической теории идеальной пластичности, предельному равновесию оболочек вращения и теории упрочняющегося пластического тела. Автор более 120 научных трудов, среди которых монографии «Теория идеальной пластичности», «Теория уплотняющегося пластического тела», «Метод возмущений теории упруго-пластичного тела», 30 авторских свидетельств на изобретения.
Высокий уровень математических исследований прикладного характера в МВТУ базировался на прочном теоретическом фундаменте, в создании которого на кафедре высшей математики училища участвовали многие видные математики, в том числе профессора Московского университета С.П. Фиников, А.Я. Хинчин, А.О. Гельфонд, Л.А.Тумаркин, работавшие в училище в сравнительно молодом возрасте, в период своего научного расцвета.
 

В конце 19 – начале 20 века на кафедре работал Леонид Кузьмич Лахтин (1863-1927), российский математик, специалист в области решения алгебраических уравнений высших степеней, а также в области математической статистики. Заслуженный профессор Московского университета, ректор Московского университета (1904—1905), декан Физико-математического факультета Московского университета (1912—1918). Его магистерская диссертация «Алгебраические уравнения, разрешимые в гипергеометрических функциях» посвящена исследованию уравнений 3-й, 4-й, 5-й и одного вида 6-й степени. В 1897 году он защитил докторскую диссертацию «Дифференциальные резольвенты алгебраических уравнений высших родов».
В 1924 году Л.К. Лахтин опубликовал большой учебник по теории вероятностей.

Известный специалист в области дифференциальной геометрии Сергей Павлович Фиников (1883-1964), работая на кафедре с 1913 г., в 1920-е годы возглавлял математическую подготовку на инженерно-строительном и электромеханическом факультетах МВТУ. Первые работы С.П. Финикова посвящены поиску главных оснований для заданного линейного элемента поверхности. Им исследовано изгибание поверхностей на кинематическом основании. Он был одним из первых геометров, перешедших в своих исследованиях на метод внешних дифференциальных форм. С.П. Фиников сыграл большую роль в распространении идей и методов Картана. В 1948 году вышла его монография «Метод внешних форм Картана», в которой наряду с изложением теории Картана, а также работ Рикье и Томаса, изложены методы определения характеристических многообразий и особых решений систем дифференциальных уравнений.

В 1929-1930 гг. кафедрой высшей математики училища заведовал Александр Яковлевич Хинчин (1894-1959), один из создателей советской школы теории вероятностей, избранный в 1939 г. членом-корреспондентом АН СССР. Он перенес методы метрической теории функций в теорию чисел и теорию вероятностей, открыл закон повторного логарифма, заложил основы теории случайных процессов, разработал методы теории массового обслуживания, использовал методы теории вероятностей в качестве математического аппарата статистической физики. А.Я.Хинчин является автором ряда учебников и учебных пособий по математике, выдержавших по три-четыре издания, а «Элементарное введение в теорию вероятностей», написанное им в соавторстве с Б.В.Гнеденко, издавалось 9 раз.

В 1931 г. кафедру возглавлял Александр Осипович Гельфонд (1906-1968) — специалист в области теории чисел, теории функций комплексного переменного и конечно-разностных методов. Ему удалось установить глубокие связи между аналитическими свойствами функций комплексного переменного и теорией чисел и создать аналитические методы доказательства трансцендентности чисел. В работах 1929 г. и 1934 г. им была решена седьмая проблема Гильберта о трансцендентности чисел специального вида, а затем доказан ряд теорем о взаимной трансцендентности чисел. В теории функций ему принадлежат работы по интерполированию целых функций и связи между ростом целых функций и арифметическими свойствами их значений. В 1939 г. А.О. Гельфонд был избран членом-корреспондентом АН СССР.
 

В 1931-1936 гг. кафедрой заведовал Лев Абрамович Тумаркин (1904-1974). У нас в стране и за рубежом он известен своими работами в области топологии, и прежде всего по теории размерности, которые публиковались начиная с 1925 г. Одним из его наиболее важных результатов является решение поставленной П.С.Урысоном проблемы о возможности разбиения компакта n-мерным подкомпактом. Л.А. Тумаркин показал, что все основные факты теории размерности, установленные в категории компактов, справедливы и вне этой категории, поскольку найденные им доказательства не используют условий компактности, а требуют лишь метризуемости пространства и наличия в нем счетной базы.
С 1930 г. на кафедре работал, а в период 1941-1952 гг. заведовал кафедрой доктор физ.-мат. наук, проф. Адольф (Андрей) Павлович Юшкевич (1906-1993) — видный историк математики, инициатор издания трудов многих классиков математики, один из основателей и ответственный редактор сборников «Историко-математические исследования», президент Международной академии истории науки (1965-1968). Он много сделал для установления тесных научных и методических связей кафедры высшей математики МВТУ с ведущими математическими кафедрами вузов страны, что способствовало высокому уровню научных исследований и преподавания математики в училище.

Влияние научного потенциала кафедры высшей математики на качество математической подготовки в училище и на уровень методического обеспечения математических курсов прослеживается, начиная с деятельности А.В. Летникова. В 1888 г. кафедру возглавил проф. Николай Александрович Шапошников (1851-1920), курсы лекций которого были для своего времени образцовыми, а составленные им учебные пособия долгое время являлись основными почти во всех технических вузах России. Он, как и А.В.Летников, интересовался вопросами методики преподавания элементарной математики и ее связью с методикой преподавания высшей математики. Н.А.Шапошников являлся автором ряда учебников по элементарной и высшей математике («Курс арифметики», «Основания общей арифметики и алгебры», «Основания теории детерминантов», «Курс тригонометрии», «Алгебра», «Основной курс математического анализа»), а составленный им в соавторстве с Н.К.Вальцевым «Методический сборник алгебраических задач» выдержал с 1887 г. по 1917 г. 24 издания, а после 1917 г. — еще 28 изданий.
Одним из лучших исследований Н.А.Шапошникова является оригинальная работа «Интегрирование дифференциальных уравнений с полными дифференциалами и частными производными первого порядка», содержащая достаточно общий прием упрощения исходного уравнения и сведения его к стандартному виду. Под руководством Н.А.Шапошникова профессорами кафедры были подготовлены и изданы важнейшие курсы: «Курс аналитической геометрии» К.А.Андреева, «Анализ и аналитическая геометрия» Д.Н.Горячева, «Математический анализ» Е.А.Болотова, курсы по аналитической геометрии Л.К.Лахтина.
Вот что вспоминал об этом времени выпускник, а позднее профессор, заведующий кафедрой теоретической механики В.П.Ветчинкин: «После ухода из МТУ преподавателя Н.А.Шапошникова Е.А. Болотов занял его кафедру высшего анализа, передав кафедру аналитической геометрии заслуженному профессору К.А.Андрееву. Несмотря на это, еще долгое время основным руководством для студентов по аналитической геометрии служил литографированный курс Е.А. Болотова.»
Что касается курса математического анализа, то учебник Н.А.Шапошникова (достаточно полный, но сухой по изложению и несколько трудный для понимания) быстро был вытеснен двухтомным литографированным курсом Е.А.Болотова, который отличался оригинальностью изложения и содержал важные для практических приложений сведения — например, вывод весьма удобной формулы квадратур Понселе, которого не присутствуют ни в одном из курсов анализа других авторов, русских и иностранных, есть более 30 таких курсов — как общих, так и специально посвящен­ных приближенным вычислениям.
В годы революции Н.А. Шапошников, уже вышедший на пенсию, оказался в Геленджике, где преподавал в женской гимназии. В сентябре 1918 он был приглашен Б.Л. Розингом в Екатеринодар (ныне Краснодар), где стал ректором только что открывшегося Северо-Кавказского политехнического института и его профессором математики. Н.А. Шапошников отстаивал сохранение СКПИ, когда над ним нависла угроза закрытия со стороны белоказачьих властей, в частности, в своей статье «Два законопроекта», опубликованной газетой «Кубанский край» (15 ноября 1918).
После 1917 г. кафедра высшей математики МВТУ играла заметную роль в организации и совершенствовании математического образования в вузах страны. В 1920-х годах при унификации в стране учебных планов подготовки инженеров-механиков по курсу высшей математики за основу был принят учебный план механического факультета МВТУ, представленный и обоснованный деканом этого факультета И.И.Куколевским. В период введения в учебный процесс всевозможных неопробированных новаций научно-педагогическая общественность училища настояла на сохранении лекционной формы обучения, в том числе по математике и другим обще­научным дисциплинам. Представители кафедры активно участвовали в многочисленных дискуссиях по проблемам преподавания математики в вузах (см., например, журналы «Естествознание и марксизм», 1930, №2,3 и «Вестник высшей школы», 1941, № 5) и последовательно отстаивали свои позиции. Научно-методические работы преподавателей кафедры регулярно публиковались в сборниках трудов, издававшихся в МВТУ.
Накопленные на кафедре в процессе преподавания методические материалы после тщательного отбора и длительной апробации использовались в многочисленных учебных пособиях для студентов. В частности, опыт ведения практических занятий по математике был обобщен в изданном в 1944 г. в МВТУ «Задачнике по высшей математике», подготовленном большим коллективом преподавателей кафедры, в который входил и погибший в декабре 1941 г. в ополчении С.Ф.Шурлапов. Этот задачник выдержал четыре издания и на его основе был составлен в 1959 г. под редакцией проф. Б.П.Демидовича сборник «Задачи и упражнения по математическому анализу для втузов». Сборник содержал более 3000 задач по всем основным разделам втузовского курса математики (за исключением аналитической геометрии) с ответами, методическими указаниями и решениями типовых примеров. Он переиздавался десять раз, был переведен на французский, испанский и португальский языки. Его авторами были преподаватели, в разное время работавшие на кафедре высшей математики МВТУ: Г.С.Бараненков, Б.П.Демидович, В.А.Ефименко, С.М.Коган, Г.Л.Лунц, Е.Ф.Поршнева, Е.П.Сычева, С.В.Фролов, Р.Я.Шостак, А.Р.Янпольский.
Длительный период методического совершенствования математической подготовки будущих инженеров в МВТУ был отражен в написанном доцентами кафедры Сергеем Васильевичем Фроловым и Родионом Яковлевичем Шостаком «Курсе высшей математики», выпущенном двумя изданиями (в 1966 г. и 1973 г.), а в 1968 г. вышло учебное пособие Р.Я.Шостака по операционному исчислению.
В 1973 г. из состава кафедры высшей математики выделилась кафедра прикладной математики, которую возглавил лауреат Государственной премии СССР д-р техн. наук, проф. Р.С.Судаков.

Кафедру «Высшая математика» возглавил д-р физ.мат. наук, проф. Михаил Сергеевич Яров-Яровой (1929–2004) известный математическими работами в области небесной механики, математики и численного интегрирования. Он разработал аналитическую теорию полетов космического корабля к Луне, выполнил исследование движения больших планет, провел численное интегрирование уравнений движений по уточненным формулам с использованием высших производных от решения, вывел новые представления потенциала небесных тел в эллипсоидальных координатах.

 

 

Современная история кафедры «Высшая математика»

В 1976 г. кафедру «Высшая математика» возглавил Геннадий Дмитриевич Карташов (1938–2008), заслуженный деятель науки Российской Федерации, крупный специалист в области ускоренных испытаний технических систем на надежность. Его кандидатская диссертация была посвящена решению проблемы восстановления многомерной функции распределения по ее известным маргинальным распределениям (если это возможно) или в оценке ее некоторых характеристик. В 1980 году Г.Д. Карташов защитил докторскую диссертацию «Исследование проблемы инвариантности в теории форсированных испытаний», в которой заложил основы теории ускоренных испытаний в нашей стране. Г.Д. Карташову удалось решить ряд сложных задач, возникающих в различных областях теории надёжности. В частности, им решена проблема планирования экспериментов с ненаблюдаемыми одновременно случайными величинами, проблема инвариантности в теории надёжности, установления области применимости различных моделей расходования ресурса изделий. На основе полученных теоретических результатов при помощи метода вложенных множеств Карташовым Г.Д.разработан новый подход к прогнозированию надежности изделий. В отличие от традиционного – аппроксимации реализаций изменения технических параметров по времени – предложена аппроксимация по ансамблю. Для последовательных систем, состоящих из большого количества разнотипных элементов, предложены приближенные асимптотические методы форсированных испытаний. Показано, в частности, что для дискретных систем асимптотически выполняется модель Пальмгрена-Майнера (линейного суммирования повреждений) и форсированные испытания таких систем можно проводить в рамках линейной модели, если отказы элементов полные. Г. Д. Карташов – автор более 250 работ, среди которых монографии: Г.Д.Карташов «Принципы расходования ресурса и их использование для оценки надежности» (1984); А.И.Перроте, Г.Д.Карташов, К.Н. Цветаев «Основы ускоренных испытаний радиоэлементов на надежность» (1968); Г.Д. Карташов «Ускоренные испытания элементов и систем» (1990), а также государственных стандартов. Под руководством Г.Д.Карташова было подготовлено и защищено 18 кандидатских и 4 докторских диссертаций.
В 1997 году было проведено еще одно разделение кафедры «Высшая математика». На ее основе была образована новая кафедра «Вычислительная математика и математическая физика», которую возглавил профессор Грешилов А. А. Кафедрой «Высшая математика» продолжал до самой смерти заведовать Карташов Г. Д.

В 2008 году кафедру возглавил доктор технических наук, профессор Сидняев Николай Иванович. Сидняев Н.И. закончил Московский государственный технический университет им. Н.Э. Баумана, Московский государственный университет им. М.В.Ломоносова, аспирантуру при Московском государственном техническом университете им. Н.Э.Баумана и без отрыва от производства Академию народного хозяйства при Правительстве Российской Федерации. Автор более 200 научных трудов.
Сидняев Н.И. стажировался в ЦНИИМаш, ЦАГИ им. Н.Е. Жуковского, НПО им. Лавочкина, Институте Механики МГУ им. М.В. Ломоносова, Ecole Centrale de Lyon, l’Université Sorbonne (France). Занимался научно-исследовательской работой по оборонной тематике. Направления: аэромеханика, газовая динамика многофазных сред, механика жидкости газа и плазмы, прикладная механика, динамика полета и управления, прочностные расчеты, численные методы, разработка программных комплексов.
Руководил научно-исследовательскими темами и направлениями по отраслям машиностроения, авиационно-космической, металлургической и атомной промышленности (математическое моделирование, численные расчеты разработка устройств различного назначения и внедрение в производство). Работал с зарубежными и с отечественными фирмами по выполнению НИР. Работал по грантам Российского Фонда Фундаментальных Исследований (РФФИ), Минобразования и ряда ведомств. В настоящее время руководит Правительственной темой между МГТУ им. Н.Э. Баумана и ОАО «ГАЗПРОМ», по созданию комплекса новейших методик и программ, необходимых для вовлечения в разработку углеводородного сырья. Под его руководством подготовлена и разработана образовательная программа для госкорпорации «РОСНАНО». Сидняев Н.И. активно работал в рабочей группе аппарата правительства РФ. Занимался экспертизой документов для проектов Законов РФ.

Одно из научных направлений Сидняева Н.И. – это взаимодействия газовых сред с обтекаемыми телами. В последние десятилетия эти исследования были сосредоточены в основном на двух направлениях. Первое связано с математическим моделированием обтекания высокоскостных летательных аппаратов, второе – с научными разработками в области фундаментальных проблем сверхзвуковых и гиперзвуковых течений газа. Изучены следующие проблемы: обтекание профилей дозвуковым и трансзвуковым потоком и вычисление аэродинамических коэффициентов; обтекание профиля в системе крыла и учет взаимного влияния элементов компоновки; решение обратных задач газодинамики для определения профиля по заданным распределениям нагрузки или скорости потока по его поверхности; расчет пограничного слоя в условиях ламинарно-турбулентного обтекания с вычислением точки перехода; обтекание профилей с усложненными свойствами; расчет аэродинамических характеристик различных тел при внесении конструктивных изменений и вариациях положения элементов компоновки; оптимизация профиля.
В области фундаментальных проблем высокоскоростных течений газа значительное внимание Сидняевым Н.И. уделялось вопросам совершенствования формы быстро летящих тел с целью достижения оптимальных значений аэродинамических характеристик в условиях разрушения поверхности. Сидняевым Н.И. проведены в широкие теоретические и экспериментальные исследования в области сверх- и гиперзвукового обтекания оптимальных пространственных тел, включающих изучение структуры возмущенного течения, свойств аэродинамических характеристик при различных режимах полета и наборах геометрических параметров и создание на этой основе достаточно простых и эффективных моделей расчета, позволяющих с достаточной точностью получать оценки аэродинамического сопротивления указанных тел и проводить их оптимизацию.
Теоретически в рамках модели идеальной жидкости и экспериментально с использованием различных методов, в том числе – специального оптического метода для изучения невидимых течений. В частности, теоретически обнаружены и получили экспериментальное подтверждение топологически новые структуры конических линий тока с особенностями в ударном слое при наличии маховской конфигурации ударных волн. Показано, что при их реализации нагрузка на угловую конфигурацию в окрестности режимов обтекания с плоскими ударными волнами, лежащими в плоскости передних кромок и принадлежащими на передних кромках к сильному семейству, терпит разрыв. Построены новые типы ударных волн в конических течениях с висячими скачками уплотнения, обнаруженные в эксперименте. Обнаружены режимы автоколебаний, обусловленные отрывом пограничного слоя.
Исследовано взаимодействие ударных волн с турбулентным пограничным слоем в конических течениях и его влияние на структуру течения в ударном слое и режимы обтекания. Установлена фундаментальная общность свойств отрыва турбулентного пограничного слоя в конических и плоских потоках. Построены эмпирические соотношения, позволяющие определять положение и размер области отрыва турбулентного пограничного слоя для широкого круга типов взаимодействия конических ударных волн и систем скачков уплотнения с пограничным слоем, а также прогнозировать глобальную перестройку структуры течения в конических угловых конфигурациях. Эти результаты значительно опережают соответствующие зарубежные исследования.
Определена роль каждого из параметров геометрии в снижении сопротивления сложных тел по сравнению с эквивалентными телами вращения. Определена область изменения параметров, где сложные тела обладают значительно меньшим полным сопротивлением по сравнению с эквивалентными конусами и оптимальными степенными телами вращения. Определена область ее справедливости для характерных параметров геометрии тела и различного состояния пограничного слоя, в которой модель может быть эффективно использована для постановки и решения оптимизационных задач.
Решена проблема устойчивости полета пространственных тел, с учетом известных способов стабилизации, которая потребовала изучения ряда фундаментальных вопросов: о положении центра давления пространственных тел и его зависимости от условий полета; о возможности создания компоновок, обладающих запасом статической устойчивости без использования дополнительных стабилизирующих устройств, значительно снижающих преимущество в сопротивлении по сравнению с эквивалентными телами вращения; об аэродинамике оптимальных пространственных форм при их стабилизации вращением. Впервые поставлена задача о форме конических тел в сверхзвуковом потоке, положение центра давления которых не зависит от числа Маха и угла атаки. Найдены точные и приближенные решения, представляющие практический интерес. Построена теория конических тел, обладающих максимальным запасом статической устойчивости при различных изопериметрических условиях. Получено экспериментальное подтверждение результатов теории, в том числе обнаруженного закона подобия, что позволяет рекомендовать найденные пространственные конфигурации в качестве формы устойчивого сверхзвукового летательного аппарата с малым сопротивлением и высокими несущими свойствами, обеспечивающими быстрое затухание колебаний тела около центра масс. Построена теория оптимальных пространственных тел минимального волнового сопротивления, вращающихся в гиперзвуковом потоке. Кроме исследований, связанных с выбором оптимальных форм аппаратов, летящих с большой скоростью, Сидняевым Н.И. выполнен цикл работ по сверхзвуковому обтеканию источников тепловыделения, а также развита линейная теория обтекания осесимметричных тел в условиях поверхностного массообмена, изучено обтекание затупленных тел в широком диапазоне скоростей набегающего потока.
С использованием аналитических и численных методов выявлены новые физические эффекты взаимодействия газа с источником тепломассообмена, сформулированы новые принципы формирования сверхзвуковых потоков с нужными для приложений свойствами, проведены расчеты влияния массоподвода на аэродинамические характеристики быстро летящих тел. Показана возможность эффективного управления параметрами теплообмена с помощью двухфазного вдува на обтекаемой поверхности. Предложен новый лагранжев метод расчета течений сред, описываемых уравнениями континуума без собственных напряжений. Метод основан на привлечении дополнительных уравнений для компонент якобиана перехода от эйлеровых к лагранжевым переменным, тем самым позволяя рассчитывать все параметры среды (включая плотность) из решения обыкновенных дифференциальных уравнений на фиксированных траекториях.
Исследования по механике вязких жидкостей развиваются Сидняевым Н.И., главным образом, по трем направлениям: пограничный слой, гидродинамическая неустойчивость и переход к турбулентности, развитие и приложение численных методов к решению уравнений Навье-Стокса, Эйлера, Прандтля. В течение многих лет эти исследования проводились в связи с запросами развития аэрокосмической техники, в частности, тепловой защиты летательных аппаратов. Основу многих исследований составили работы Н.И.Сидняева по гидродинамической устойчивости аэродинамических следов, вихревых слоев и течений в каналах. Что касается численных решений задач вязкой жидкости, то исследования в этом направлении всегда были связаны с идеей об особой эффективности прямых методов Галеркина в комбинации с конечноразностными процедурами. Один из таких подходов, известный как метод Галеркина-Петрова, оказался особенно полезным не только для решения линейных задач устойчивости, но и для анализа нелинейных колебательных и волновых процессов в течениях вязкой жидкости.

Обширный цикл работ по гидродинамике вязких жидкостей на кафедре выполнен под руководством проф. Н.И.Сидняева. Продолжались традиционные для кафедры исследования фундаментальных свойств вязких потоков, дисперсных сред таких, как неустойчивость и переход к турбулентности, вихреобразование и перенос завихренности при обтекании тел конечных размеров, отрывы и автоколебания в зонах отрыва, образование и динамика поверхностей раздела и свободных поверхностей в вязких потоках, перестройки потока под воздействием внешних объемных и поверхностных сил. Выбор конкретных задач определялся актуальными запросами современной технологии, экологии, техники. Значительная часть проводимых исследований посвящена течениям со свободными поверхностями и с поверхностями раздела, в частности, капиллярным течениям в струях и пленках при различной геометрии удерживающих и формирующих поток твердых поверхностей.
Большой интерес представляют исследования Сидняева Н.И. по изучению свойств нелинейных, и особенно, сильно нелинейных волн в вязкой жидкости в условиях, когда они развиваются под воздействием сил давления в грунтах, силы тяжести и внешних воздействий. Исследование их с применением прямых методов приводит к нелинейным математическим моделям с диссипацией и дисперсией. Объект исследования составляют пограничные слои, ограниченные свободными поверхностями, и пограничные слои вблизи поверхностей раздела. Для адекватного описания движений свободной поверхности с большой амплитудой, например, сильно нелинейных волн, разработан способ соответствующего обобщения уравнений Прандтля. Выполнен большой цикл работ по аэрогидромеханике. Такие исследования включают: решение уравнений Навье-Стокса в приближении пограничного слоя для течений сред со свободными границами и границами раздела, исследование гидродинамической неустойчивости стационарных и нестационарных течений, анализ нелинейного развития возмущений и формирование волн.
Установлен ряд закономерностей фундаментального характера. Роль вязкости, формирующей профиль скорости в слое, оказывается существенной, т.к. может приводить к появлению профильной неустойчивости, отличной от неустойчивости Релея и Кельвина-Гельмгольца. Исследованы струйные течения, в которых развитием неустойчивости можно достаточно эффективно управлять с помощью наложенных вращений, геометрией удерживающей поверхности и свободной пленки. Новое развитие получила задача о пограничном слое на поверхности раздела, развивающемся под воздействием трения на поверхности. Проведенные расчеты спектров неустойчивости таких пограничных слоев открыли новые моды неустойчивости и наметили направление исследований для истолкования сложной картины турбулизации поверхности. Процессы гидродинамической неустойчивости, порождающие волновые структуры на поверхности, развиваются при сравнительно небольших числах Рейнольдса. Это обстоятельство позволяет успешно применять прямые методы для изучения динамики волновых пленок жидкости. Содержательная нелинейная модель течения построена осреднением по толщине пленки системы уравнений Навье-Стокса. Проведено численное исследование уравнений течений при задании в качестве начальных условий малых гармонических волн, а также регулярных нелинейных решений. Уравнения содержат внешний параметр, возрастающий вместе с числом Рейнольдса и средней толщиной пленки. Особое внимание уделено случаю малых волновых чисел, при которых на каждом пространственном периоде квазистационарной волны имеется четко выраженный участок невозмущенной поверхности, так что регулярная волна по существу представляет уединенную волну. Установлены общие закономерности динамики развивающихся волновых фронтов, которые заключаются в следующем. Все регулярные нелинейные волновые решения, также как малые гармонические волны, неустойчивы и автоматически перестраиваются в устойчивые волновые структуры.
В течение ряда лет на кафедре проводятся исследования по теории нелинейных волн в пленках. Решению модельных уравнений Сидняевым Н.И. посвящен целый ряд оригинальных работ и обзорных статей. Разработанные Сидняевым Н.И. методы находят эффективное приложение к изучению неустойчивости и нелинейных волн, усложненных процессами тепло- и массообмена. Анализ проблем обобщения и приложений модельных уравнений показал, что часто применяемые слабонелинейные модельные уравнения являются частными случаями модельных уравнений при стремлении к нулю единственного свободного параметра подобия, отражающего условия экспериментов. Как следствие этого, нелинейные волновые решения предельных модельных уравнений представляют лишь математические волны. Проведено подробное численное исследование нестационарных решений предельного модельного уравнения и построена наиболее полная картина динамики их развития во времени. В развитие проблемы о тепломассопереносе, выполнен ряд работ, в которых основной результат обобщен на другие случаи. В связи с нелинейностью основных уравнений численные методы играют существенную роль в аэрогидродинамике. Они применяются не только для доведения до конечного численного результата решений отдельных задач, но, главным образом, для выявления фундаментальных свойств течений. Особенно это относится к течениям вязкой жидкости. Развитие численных методов Сидняевым Н.И. ориентировано на применение прямых методов при гибком комбинировании их с методами конечных разностей. Численные методы решения линейных и нелинейных проблем гидродинамической устойчивости разрабатывались для изучения неустойчивости, нелинейного развития возмущений и переходов к сложным пространственным структурам в потоках с границами раздела и зонами отрыва, формирующихся в закрученных потоках и при обтекании плоских тел вязкой жидкостью. Исследованы критические значения параметров, при которых происходит потеря устойчивости стационарных течений, изучается нелинейный переход к новым периодическим или квазипериодическим состояниям и находятся решения уравнений Навье-Стокса для вторичных течений. В частности, решена проблема отыскания собственных чисел для системы уравнений Орра-Зоммерфельда в двух областях с условиями плавного сопряжения на границе раздела. Это создает возможность находить области неустойчивости и наиболее растущие возмущения в течениях. Численными экспериментами показано, что возможно надежное моделирование ламинарного и турбулентного закрученного течения с застойной зоной ламинарным потоком с эффективным числом Рейнольдса, которому соответствует подходящее решение уравнений Навье-Стокса. Для истолкования гидродинамических механизмов разрушения вихрей исследована неустойчивость закрученных потоков с застойной зоной, которые характеризуются тем, что основное течение не плоскопараллельное. Обнаружены новые моды для свободного вихря, изучено возникновение, исчезновение, переход мод друг в друга при изменении чисел Рейнольдса, закрутки, геометрических параметров.
Проведены исследования взаимодействий неустойчивостей и зон отрыва при обтекании профиля крыла с перфорированной и непроницаемой поверхностью дозвуковым и трансзвуковым потоком газа. Усовершенствована вычислительная схема для расчета базовой задачи об обтекании кругового цилиндра, сопровождаемым формированием нестационарной зоны отрыва с вихревой дорожкой, при учете перемещений цилиндра. Отработаны алгоритмы, программы и постановки задач, учитывающих развитие неустойчивости в пограничном слое от носика профиля до зон отрыва. Прямыми вычислениями показана возможность затягивания перехода и отрыва с помощью управляемого вдува. Включение перфорации поверхности в анализ позволяет конструировать сверхзвуковые течения, в которых зона отрыва, вызываемая размытым скачком, оказывается минимальной.
Новый нелинейный эффект обнаружен прямыми вычислениями в задаче о вторичных течениях после потери устойчивости вращающегося течения. Наряду с вихрями Тейлора, самопроизвольно развивающимися из малых возмущений, существуют также периодические структуры, которые устанавливаются при начальных возмущениях конечной амплитуды. Развиты математические модели пограничного слоя в условиях массопереноса. Широкий круг вопросов, связанных с теорией пластических деформаций, химической технологией, течениями многофазных сред, геофизикой и геологией, исследован профессором Н.И. Сидняевым, а также построена математическая модель фильтрации газа через тепловыделяющую грунтовую среду, на основе которой удалось объяснить данные наблюдений за поведением криолитозоны. Учет неньютоновских реологических свойств мантийных пород грунтов позволил воспроизвести ряд известных в геологии особенностей эволюции глобального геодинамического процесса в районах Крайнего Севера.

 

---

Кафедра «Высшая математика» сегодня

В настоящее время на кафедре «Высшая математика» работают 15 профессоров, 29 доцентов, 9 старших преподавателей, 8 ассистентов. Среди преподавателей кафедры выпускники МГУ им. М. В. Ломоносова (механико-математического, физического факультетов, факультета вычислительной математики и кибернетики), МФТИ, МГТУ им. Н. Э. Баумана, физико-математических факультетов других университетов. Более сорока лет на кафедре работают доценты Вилисова Н. Т., Крапоткин В.Г., Кузнецов В.В., Паршев Л.П., Покровский Л.Д., Янов И.О.

Доц. Паршев Л. П. в течение многих лет возглавляет предметную комиссию по математике университета.

Профсоюзный комитет кафедры возглавляет старший преподаватель Шевченко М. Н.
Доц. Крапоткин В. Г. С 1981 по 1985 г. Работал в Алжире, в институте нефтегазовой химии, а с 1985 по 1988 г. В Мали, в высшей инженерной школе.
Доц. Соболев С. К. с 1983 по 1987 г. работал в Мозамбике, заведовал кафедрой теоретической математики на математическом факультете Мозамбикского университета.
Доц. Кузнецов В. В. участвовал в создании СУНЦ (физико-математический лицей №1580 при МГТУ им. Н. Э. Баумана), а также в течение восьми лет был его директором.
Доц. Леванков В. И. в течение многих лет ведет занятия в ГУИМЦ для слабослышащих студентов.

Доц. Кузнецов В. В. является заслуженным мастером спорта СССР, бронзовым призером Олимпийских игр 1964 года, чемпионом мира 1966 года в составе сборной СССР по водному поло. Доц. Леванков В. И. является мастером спорта по бадминтону. Доц. Крапоткин В. Г. – кандидат в мастера спорта по самбо, двукратный чемпион Москвы, проф. Васильев Н. С. – мастер спорта по спортивной гимнастике.
Проф. Смольяков Э. Р. является специалистом по нетрадиционным методам сохранения и восстановления здоровья. Об этом он написал в книге «Тайны жизни. Практика умственного и физического самосовершенствования».
Проф. Ильичев А. Т. является автором справочника по русской истории.

 

---

Научная работа

Круг научных интересов специалистов, работающих на кафедре, очень широк. По ряду направлений они занимают ведущие позиции в разрабатываемых проблемах теоретической и прикладной математики. Многие результаты, полученные преподавателями кафедры, получили признание не только в нашей стране, но и за рубежом. На кафедре работает научный семинар «Динамика возмущений в сплошных средах» под руководством профессоров А. Т. Ильичева и А. С. Савина, проводятся научные конференции по актуальным направлениям развития прикладной математики в энергетике, энергоэффективности и информационно-коммуникационных технологиях.

Основными направлениями исследований на кафедре являются:

• Дифференциальные уравнения и уравнения в частных производных (проф. Филиновский А. В., доц. Гласко А. В., доц. Зорина И. Г., доц. Неклюдов А. В., доц. Станцо В. В., доц. Копаев А. В., доц. Павельева Е. Б., доц. Покровский Л. Д., доц. Аникин А. Ю.).
• Теория вероятностей, математическая статистика, математическая теория надежности (проф. Белов В. Н., доц. Ветров Л. Г., проф. Калинкин А. В., проф. Павлов И. В., проф. Тимонин В. И., доц. Сунчалина А. Л.).
• Исследование операций (проф. Васильев Н. С., проф. Грешилов А.А., проф. Смольяков Э.Р.).
• Функциональный анализ и алгебра (проф. Исмагилов Р. С., доц. Табалдыев С. Б., доц. Храпов П. В., доц. Огнева О. С.).
• Механика сплошной среды (проф. Ильичев А.Т., проф. Савин А. С., проф. Сидняев Н. И., доц. Томашпольский В. Я., доц. Федотов А.А., проф. Шахов Е. М., доц. Богомолов В. Г., доц. Бояринцева Т. Е., доц. Янов И. О.).
• Теория атомарных и R – функций, вейвлеты, фракталы (проф. Кравченко В. Ф., ст. преп. Коновалов Я.Ю.).

 

Фундаментальные научные направления

1. Дифференциальные уравнения и уравнения в частных производных.

Профессор Филиновский Алексей Владиславович, доктор физико-математических наук, крупный специалист в области уравнений математической физики. Он автор более 100 научных работ, им опубликованы 2 монографии по исследуемой тематике. Его научные результаты относятся к решению задач стабилизации при больших значениях времени решений нестационарных смешанных задач для эллиптических операторов в неограниченных областях; исследованию экстремальных задач для уравнений в частных производных; изучению спектральных свойств несамосопряженных краевых задач. Среди главных результатов:

• изучено асимптотическое поведение при больших значениях времени решений внешних краевых задач для нестационарных уравнений высокого порядка;
• получены интегральные оценки скорости убывания решений первой смешанной задачи для волнового уравнения в областях с компактными незвездными границами;
• получены равномерные по спектральному параметру оценки резольвентны первой краевой задачи для оператора Лапласа и ее производной по спектральному параметру в неограниченных областях;
• получено достаточное условие непрерывности спектра первой краевой задачи для полигармонического оператора в областях с некомпактными границами;
• изучены классы существования решений экстремальных задач с несамосопряженными краевыми условиями для параболических уравнений.

Результаты исследований частично изложены в монографиях:

• Асташова И.В., Кондратьев В.А., Муравей Л.А., Филиновский А.В. Качественная теория дифференциальных уравнений. – М.: МАТИ-РГАТУ, 2001. – 141с.
• Astashova I.V., Filinovskii A.V., Kondratiev V.A., Muravey L.A. Some Problems in Qualitative Theory of Differential Equations. – London.; Jnan Bhawan Publishers, 2002.

Доцент Гласко Андрей Владленович, кандидат физико– математических наук, автор около 30 научных работ.
Область научных интересов Гласко А.В. распространяется на использование уравнений математической физики для создания математических моделей, моделирующих как поведение живых систем, так и процессы самоорганизации искусственных систем (в частности, наноматериалы).
К основным результатам относятся:
- создана и частично обоснована математическая модель динамики внимания в процессе восприятия элементарного внешнего стимула;
- разработка модели конвергентных процессов, имеющей приложения в процессе описания самоорганизации материи и самосборки наноструктур, представляющих основу восходящих технологий.
Доцент Павельева Елена Борисовна, кандидат физико – математических наук, автор около 10 научных работ. Занимается исследованием асимптотических свойств решений уравнения переноса излучения в неодномерных протяженных цилиндрических областях.
На основе асимптотической теории разработаны алгоритмы поиска асимптотических режимов в протяженных неодномерных цилиндрических областях и получены тестовые результаты для радиационных полей в задачах о глубоко проникающем излучении.

Доцент Неклюдов Алексей Владимирович, кандидат физико – математических наук. Область научных интересов – изучение поведения решений эллиптических уравнений, в т.ч. нелинейных, в неограниченных областях. Получены результаты по поведению решений задачи Неймана для уравнений произвольного порядка в областях, близких к цилиндрическим. Исследованы особенности решений в цилиндрической области нелинейного уравнения второго порядка с экспоненциальной нелинейностью. Результаты исследований опубликованы в нескольких статьях журналов АН Российской Федерации.

Доцент Станцо Виталий Владимирович, кандидат физико–математических наук. Он является специалистом по качественной теории дифференциальных уравнений. Его исследования посвящены исследованию возникновения предельных циклов в трехпараметрических двумерных динамических системах. В частности, ему принадлежит результат, показывающий, что количество таких циклов в ограниченной области может быть сколь угодно большим. Интенсивно занимается вопросами приложений дифференциальных уравнений в экономико-математическом моделировании. Станцо В.В. опубликовал 20 научных работ по теоретическим и прикладным вопросам теории дифференциальных уравнений.
Доцент Зорина Ирина Григорьевна, кандидат физико – математических наук. Имеет более 10 научных публикаций по исследованию процессов теплообмена при фазовопереходных процессах в различных средах. Получены интересные результаты в теории подобия систем плазменной аэродинамики. Ее работы нашли практическое применение, в частности, при оптимизации ультразвуковых составных электроакустических преобразователей для обработки инфицированных ран.

Доцент Покровский Леонид Дмитриевич, кандидат физико – математических наук. Высококвалифицированный специалист по задачам газовой динамики с нелинейной теплопроводностью, теории пограничного слоя. Его главные результаты относятся к области классификации и свойств решений уравнения переноса с нелинейностями общего вида (включая турбулентную фильтрацию).
Леонид Дмитриевич в совершенстве владеет французским языком, что позволяет ему регулярно принимать участие в научных конференциях во Франции. Автор около 40 научных и методических работ. Он подготовил 3 кандидата физико – математических наук (среди них доцент кафедры Гласко А. В.).

Доцент Копаев Анатолий Владимирович – кандидат физико – математических наук. Его научные интересы сосредоточены в области решения краевых задач теории аналитических функций (одной и нескольких переменных) и их применения в математической физике. Им предложен универсальный метод «функциональных уравнений» для решения задач сопряжения аналитических и гармонических функций, возникающих при описании установившихся фильтрационных течений несжимаемой жидкости в кусочно-однородных средах. Для решения одного из важнейших функциональных уравнений удалось построить интегро-дифференциальное преобразование, которое каждой гармонической в полупространстве функции трех переменных ставит в соответствие гармоническую в полуплоскости функцию двух переменных, зависящую от одного действительного параметра, а также найдено обратное преобразование. А.В. Копаевым опубликовано более 20 работ по данной тематике.

Доцент Аникин Анатолий Юрьевич, кандидат физико – математических наук, ведет исследования в области динамических систем классической механики. Основные направления его работы: гамильтонова динамика; хаос и интегрируемость в гамильтоновой динамике; локальные методы в гамильтоновой динамике; квазиклассический анализ; квантовая и статистическая механика с точки зрения классической. Им опубликованы три работы в зарубежных изданиях, в которых, в частности, доказан квантовый аналог теоремы Мозера о сходимости нормализующего преобразования для случая полутора степеней свободы; получен альтернативный язык, более алгебраический по сравнению со стандартным, для канонического формализма в неавтономном случае; получен квантовый аналог этого языка.

 

2. Теория вероятностей, математическая статистика, математическая теория надежности.
На кафедре сложился сильный коллектив специалистов, работающих в области теории вероятности и математической статистики, а также научных и технических приложений этих направлений. В частности, в области планирования, проведения и анализа результатов ускоренных испытаний, оценки надежности изделий в переменных режимах, а также прогнозирования показателей надежности сложных систем кафедра является одним из основных центров разработки новых идей и направлений.

Профессор Белов Владимир Николаевич, доктор технических наук, автор 60 научных работ и 2 монографий. Является известным специалистом в области оценки показателей надежности сложных технических систем. Основное направление исследований: моделирование (скалярное, векторное) временных процессов различной природы.
Полученные результаты:

• построены функционалы специального вида, позволяющие (при достаточно общих ограничениях на временной процесс) осуществлять пересчеты характеристик процесса от одних условий реализации к другим (статический, циклический, динамический режимы). Это позволило построить методы прогнозирования характеристик временного процесса в условиях (статических, циклических), требующих проведения длительных экспериментов, по результатам кратковременных испытаний (например, в динамических режимах);
• разработана процедура построения режима изменения внешних условий, обеспечивающего изменение требуемой характеристики процесса по заданной (но реализуемой) траектории;
• разработаны методы прогнозирования показателей надежности изделий радиоэлектроники в условиях эксплуатации по результатам лабораторных испытаний.

Частично результаты исследований представлены в двух монографиях:

• Белов В.Н. Детерминированные модели временных процессов. – Волгоград: Политехник, 2002;
• Белов В.Н. Стохастические модели временных процессов. – Волгоград: Политехник, 2002.

Доцент Ветров Леонид Георгиевич, кандидат физико – математических наук. Являясь специалистом по теории вероятности (основные работы относятся к теории фильтрации мартингалов), он получил ряд интересных результатов в самых разнообразных прикладных областях. Им, в частности, исследовались вопросы построения системы бонус – малус в задачах автострахования; разработаны модели и методы проведения форсированных испытаний сложных систем и систем «без памяти»; получены модели поведения игроков на финансовом рынке валютных «фьючерсов». По этим направлениям им опубликовано более 40 научных публикаций в нашей стране и за рубежом.

Профессор Калинкин Александр Владимирович, доктор физико-математических наук. Опубликовал около 60 научных работ по исследованию и моделированию стохастических систем с взаимодействием с марковскими процессами при дискретных состояниях.
Разработанные им схемы взаимодействия широко используются для исследования вероятностных объектов физической кинетики, химической кинетики, экологии, в теории надежности технических систем (на рис. 2 представлены фазовая плоскость (а) и гистограмма (б)). Основные результаты:

• введены и классифицированы общие марковский процессы со взаимодействием при счетном множестве состояний на основе схемы взаимодействий;
• разработаны новые методы решения уравнений Колмогорова для производящих функций переходных вероятностей в нестационарном и стационарном случаях;
• для ряда процессов со взаимодействием выявлено нелинейное свойство (кинетическое уравнение) переходных вероятностей путем построения точных замкнутых решений первого и второго (линейных) уравнений Колмогорова.

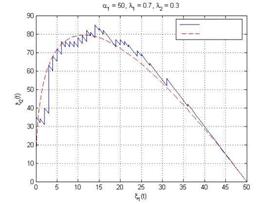
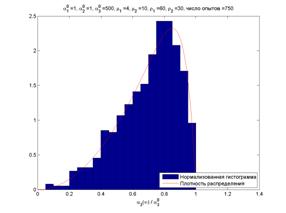
Полученные результаты: найдены решения первого и второго (линейных) уравнений Колмогорова для специальных классов марковских процессов: ветвящихся процессов, ветвящихся процессов с взаимодействием и других. Марковские процессы с взаимодействием определяются как модели эволюции систем частиц нескольких типов, согласно данной кинетической схеме. В случае независимости эволюций отдельных частиц друг от друга известно обыкновенное нелинейное дифференциальное уравнение для одночастичной производящей функции переходных вероятностей (кинетическое уравнение для одночастичной функции распределения). Фундаментальная проблема вывода третьего (нелинейного) уравнения теории марковских процессов разрешима через построение точных замкнутых решений линейных уравнений Колмогорова. Результаты исследований частично изложены в монографии “Markov’s branching processes with interaction”, Russian Mathematical Surveys, 2002, v. 57, p. 241-304.

Профессор Павлов Игорь Валерианович, доктор физико-математических наук. Лауреат премии правительства РФ в области науки и техники за 2003 г. Видный специалист в области оценки и прогноза надежности больших технических систем на основе данных по испытаниям их компонент (элементов, подсистем). Его научные результаты отражены более чем в 60 научных трудах, а также в двух монографиях. Одним из основных направлений научной работы кафедры высшей математики (ФН -1) является математическая теория надежности и ряд связанных с ней направлений:

• Надежность и безопасность сложных технических систем, таких как современные системы энергетики, транспортные сети, системы радиоэлектроники, приборостроения и др.
• Испытания сложных технических систем
• Ускоренные испытания
• Оценка остаточного ресурса сложных технических систем

Математическая теория надежности как система соответствующих идей, математических моделей и методов оценки, прогноза и оптимизации показателей надежности, начала развиваться в послевоенные годы в связи с возрастающими требованиями к новой сложной технике. В 50-х годах вопросы надежности, испытания на надежность и задачи повышения надежности ракет и электронного оборудования стали привлекать значительное внимание, как математиков, так и инженеров – разработчиков новой техники. После чего в последующие годы появилось значительное число работ в этой области, в основном российских и американских ученых. При этом многие исследования шли параллельно и в некоторых вопросах удалось продвинуться дальше американским специалистам, а в некоторых – нашим. Основные работы сотрудников кафедры высшей математики МГТУ им. Н.Э.Баумана в области математической теории надежности и смежных областях.
Научные результаты: