Перейти к списку | Аннотация | Содержание
 Аннотация
Аннотация
Книга является шестым выпуском комплекса учебников «Математика в техническом университете». Знакомит читателя с понятиями неопределенного и определенного интегралов и методами их вычисления. Уделено внимание приложениям определенного интеграла, приведены примеры и задачи физического, механического и технического содержания.
Содержание учебника соответствует курсу лекций, который автор читает в МГТУ им. Н.Э. Баумана.
Для студентов технических университетов. Может быть полезен преподавателям и аспирантам.
Содержание
| Предисловие | ||
| Основные обозначения | ||
| 1. | Неопределенный интеграл | |
| 1.1. | Вводные замечания | |
| 1.2. | Понятия первообразной и неопределенного интеграла | |
| 1.3. | Свойства неопределенного интеграла | |
| 1.4. | Основные неопределенные интегралы | |
| 1.5. | Интегрирование подстановкой и заменой переменного | |
| 1.6. | Интегрирование по частям | |
| Д.1.1. | Первообразная непрерывной функции | |
| Вопросы и задачи | ||
| 2. | Интегрирование рациональных дробей | |
| 2.1. | Дробно-рациональные подынтегральные функции | |
| 2.2. | Интегралы от простейших рациональных дробей | |
| 2.3. | Разложение правильной рациональной дроби на простейшие | |
| 2.4. | Интегрирование дробно-рациональных функций | |
| Д.2.1. | Метод Остроградского | |
| Д.2.2. | Интегрирование рациональных функций, содержащих биномы | |
| Вопросы и задачи | ||
| 3. | Интегрирование иррациональных выражений | |
| 3.1. | Рациональные функции от радикалов | |
| 3.2. | Интегрирование функций, содержащих радикалы от дробно-линейной функции | |
| 3.3. | Подстановки Эйлера | |
| 3.4. | Другие приемы интегрирования | |
| 3.5. | Тригонометрические и гиперболические подстановки | |
| 3.6. | Интегралы от дифференциального бинома | |
| Д.3.1. | Геометрический смысл подстановок Эйлера | |
| Д.3.2. |
Об интегрировании функций вида 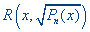 |
|
| Вопросы и задачи | ||
| 4. | Интегралы от некоторых трансцендентных функций | |
| 4.1. | Рациональные функции синуса и косинуса | |
| 4.2. | Рациональные степени синуса и косинуса | |
| 4.3. | Экспоненциальные и гиперболические функции | |
| 4.4. | Различные трансцендентные выражения | |
| Вопросы и задачи | ||
| 5. | Интеграл Ньютона | |
| 5.1. | Понятие определенного интеграла Ньютона | |
| 5.2. | Формула Ньютона - Лейбница | |
| 5.3. | Свойства интеграла Ньютона | |
| 5.4. | Теорема о среднем значении и ее следствия | |
| 5.5. | Интеграл Ньютона с переменными пределами | |
| 5.6. | Геометрическая и механическая интерпретации интеграла Ньютона | |
| 5.7. | Способы вычисления интеграла Ньютона | |
| Вопросы и задачи | ||
| 6. | Определенный интеграл | |
| 6.1. | Интегральная сумма и ее предел | |
| 6.2. | Интеграл Римана | |
| 6.3. | Суммы и интегралы Дарбу | |
| 6.4. | Критерий существования определенного интеграла | |
| 6.5. | Классы интегрируемых функций | |
| 6.6. | Свойства интегрируемых функций | |
| 6.7. | Основные свойства определенного интеграла | |
| 6.8. | Теоремы о среднем значении для определенного интеграла | |
| 6.9. | Определенный интеграл с переменным пределом | |
| 6.10. | Вычисление определенного интеграла | |
| Д.6.1. | Доказательство теорем о классах интегрируемых функций | |
| Д.6.2. | Доказательство теорем 6.19 и 6.20 | |
| Д.6.3. | Связь интегралов Ньютона и Римана | |
| Д.6.4. | Обобщение теорем о среднем значении | |
| Вопросы и задачи | ||
| 7. | Несобственные интегралы | |
| 7.1. | Интегралы по бесконечному промежутку | |
| 7.2. | Основные свойства сходящихся несобственных интегралов по бесконечному промежутку | |
| 7.3. | Признаки сходимости интегралов по бесконечному промежутку | |
| 7.4. | Интегралы от неограниченных функций | |
| 7.5. | Сходимость интегралов от неограниченных функций | |
| 7.6. | Абсолютная и условная сходимость несобственных интегралов | |
| 7.7. | Другие признаки сходимости несобственных интегралов | |
| 7.8. | Примеры исследования несобственных интегралов на сходимость | |
| 7.9. | Преобразование несобственных интегралов | |
| 7.10. | Главные значения несобственных интегралов | |
| Вопросы и задачи | ||
| 8. | Интегралы, зависящие от параметра | |
| 8.1. | Определенные интегралы, зависящие от параметра | |
| 8.2. | Дифференцирование интегралов по параметру | |
| 8.3. | Интегрирование по параметру | |
| 8.4. | Равномерная сходимость несобственных интегралов | |
| 8.5. | Признаки равномерной сходимости несобственных интегралов | |
| 8.6. | Непрерывность и дифференцируемость несобственных интегралов по параметру | |
| 8.7. | Интегрирование несобственных интегралов по параметру | |
| 8.8. | Эйлеровы интегралы | |
| Вопросы и задачи | ||
| 9. | Приложения определенного интеграла | |
| 9.1. | Общая схема применения интеграла | |
| 9.2. | Длина кривой | |
| 9.3. | Площадь плоской фигуры | |
| 9.4. | Объем тела | |
| 9.5. | Площадь поверхности | |
| 9.6. | Вычисление масс и моментов инерции | |
| 9.7. | Статические моменты и координаты центра масс | |
| 9.8. | Работа, энергия, сила давления | |
| Д.9.1. | Движение материальной точки в центральном поле тяготения | |
| Вопросы и задачи | ||
| 10. Численное интегрирование | ||
| 10.1. | Существо подхода к численному интегрированию | |
| 10.2. | Формула трапеций | |
| 10.3. | Формула парабол | |
| 10.4. | Формулы прямоугольников | |
| 10.5. | Приближение многочленами высших степеней | |
| 10.6. | Квадратурная формула Гаусса | |
| 10.7. | Практическая оценка погрешности численного интегрирования | |
| 10.8. | Учет особенностей поведения подынтегральной функции | |
| 10.9. | Приближенное вычисление несобственных интегралов | |
| 10.10. | Особенности вычисления неопределенных интегралов | |
| Вопросы и задачи | ||
| Приложение. Таблица неопределенных интегралов | ||
| Список рекомендуемой литературы | ||
| Предметный указатель | ||



