Глава 6. Магнитные цепи при постоянной

 

магнитодвижущей силе (МДС).

6.1. Введение.

Магнитная цепь (МЦ) – часть электротехнического устройства, предназначенного для создания в определенном месте пространства магнитного поля требуемой интенсивности и направленности. Магнитные цепи составляют основу практически всех электротехнических устройств и многих измерительных приборов.

В составе МЦ имеются элементы, возбуждающие магнитное поле (одна или несколько намагничивающих обмоток или постоянные магниты) и магнитопровод, выполненный в основном из ферромагнитных материалов. Использование ферромагнетиков обусловлено их способностью многократно усиливать внешнее (по отношению к ним) магнитное поле, создаваемое намагничивающими обмотками или постоянными магнитами. Ферромагнетики отличает высокая магнитная проницаемость по сравнению с окружающей средой, что дает возможность концентрировать и направлять магнитные поля.

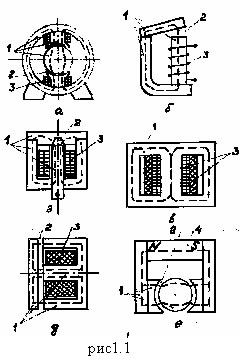
На рис. 1.1 в качестве примера представлены МЦ некоторых электромагнитных устройств:  а – машин постоянного тока, б – электромагнитного реле,  в – трансформатор, г и д  –  тормозных электромагнитов, е  – магнитоэлектрического измерительного прибора. Цифрой 1- обозначены ферромагнитные части магнитопроводов, 2 – воздушные зазоры, 3 – намагничивающие катушки, 4 – постоянный магнит.

 

 

МЦ с постоянной МДС называются цепи, в которых магнитное поле возбуждается постоянными токами намагничивающих обмоток или постоянными магнитами.

При анализе и расчете магнитных цепей пользуются следующими величинами, характеризующими магнитное поле:

– вектор магнитной индукции. Характеризует интенсивность и направленность магнитного поля в данной точке пространства. Единица измерения – тесла (1 Тл =1 = 1 )

– вектор напряженности магнитного поля в данной точке. Единица измерения – ампер на метр (А/м).

Отношение – абсолютная магнитная проницаемость. Для вакуума, а также для любых неферромагнитных материалов принимается равной  m0= 4π·10-7  Гн/м; отношение – относительная магнитная проницаемость ( для конкретных ферромагнетиков может доходить до 104 – 106 ).

Ф – магнитный поток – поток вектора магнитной индукции через площадь S (рис. 1.1), единица измерения вебер (1Вб=1Тл×1м2).

1.1.

В случае однородного магнитного поля, когда B=const в любой точке поля и вектор магнитной индукции  ^S  (Ða=0),  магнитный поток

Ф=B×S     1.2.

Расчет магнитной цепи невозможен, если неизвестна основная кривая намагничивания (ОКН) ферромагнетика, используемого в магнитопроводе.

ОКН задается в справочной литературе на электротехнические материалы как зависимость В(Н)  либо в табличной форме, либо графически (рис. 1.3).

Отметим, что  на участке оа, отношение const. – магнитная цепь не насыщена. При дальнейшем увеличении Н темп увеличения индукции В снижается и прекращается полностью, когда наступает магнитное насыщение материала магнитопровода.

 

↑ Вверх, к содержанию раздела ↑

6.2. Законы магнитных цепей.

Наиболее общим законом является закон полного тока. Этот закон устанавливает взаимосвязь между напряженностью магнитного поля и вызвавшим её током.

Формулировка закона:

Линейный интеграл от вектора напряженности по замкнутому контуру равен алгебраической сумме токов, охватываемых этим контуром – полному току (Iполн).

При определении полного тока в уравнение закона полного тока со знаком «+» следует включать токи, положительные направления которых связаны с произвольно выбранным направлением обхода правилом правоходового винта.

На рис. 1.4 контур интегрирования пронизывает три отдельных витка с токами I1, I2, I3.

 

рис.1.4

Закон полного тока 1.3.

Для практических целей наибольший интерес представляет частный случай, когда контур интегрирования проходит внутри обмотки с числом витков w и током I (рис. 1.5) В этом случае полный ток .

 

 

Произведение (w×I) называют магнитодвижущей силой (МДС). МДС возбуждает магнитный поток Ф в магнитной цепи подобно тому, как ЭДС возбуждает ток в электрической цепи.

Как и ЭДС, МДС является величиной направленной, ее положительное направление указывается на схеме. Положительное направление МДС  w×I принимают совпадающим с поступательным движением правоходового винта, если вращать его по направлению тока в обмотке.

Удобно использовать и другое правило для определения направления МДС обмотки, а именно: если мысленно обхватить правой рукой сердечник, расположив пальцы по направлению тока, то отогнутый большой палец покажет направление МДС (рис. 1.6).

 

 

↑ Вверх, к содержанию раздела ↑

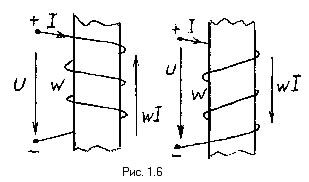6.3. Магнитное напряжение на участке магнитной цепи.

Магнитным напряжением между точками а и b магнитной цепи называют линейный интеграл от вектора напряженности магнитного поля между этими 1.4.

Если на участке магнитной цепи H=const и совпадает по направлению с элементом пути обхода , то

1.5.

Если принять в внимание, что Н=В/mа, где mа – абсолютная магнитная проницаемость, а В=Ф/S, то формулу 1.5 магнитного напряжения можно представить в виде

,       1.6.

где – магнитное сопротивление.

Выражение 1.6 называют законом Ома для магнитной цепи по аналогии с электрической цепью (поток Ф – аналог тока I, Rm – аналог электрического сопротивления R). Так же, по аналогии с электрической цепью и закон полного тока, представленный в виде

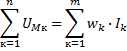, 1.7.

называют вторым законом Кирхгофа для магнитной цепи (алгебраическая сумма магнитных напряжений вдоль любого замкнутого контура равна алгебраической сумме МДС).

↑ Вверх, к содержанию раздела ↑

6.4. Задачи расчета магнитных цепей.

Существует два типа задач, а именно:

прямая задача – по заданному значению потока Ф определяют МДС w×I обмотки;

2.обратная задача - задается значение МДС w×I и требуется определить поток Ф.

В обоих случаях должны быть известны геометрические размеры магнитопровода (длины l и площади поперечных сечений S всех участков магнитопровода), материалы участков и кривые намагничивания.

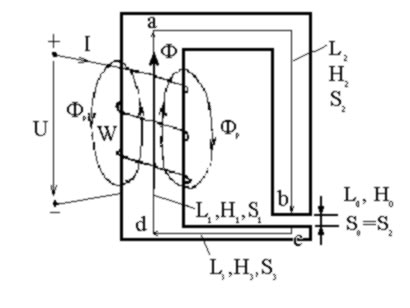
Для упрощения расчета пренебрегают магнитными потоками рассеяния Фр (рис. 1.8) и не учитывают выпучивание магнитного поля в воздушных зазорах, считая площадь сечения воздушного зазора S0 (рис. 1.8) равной площади поперечного сечения ферромагнитного магнитопровода.

 

рис.1.8.

6.4.1. Решение прямой задачи.

6.4.1.1. Неразветвленная магнитная цепь.

Пример подобной цепи представлен на рис. 1.8.

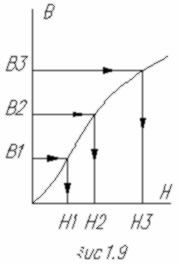
Эту цепь можно разбить на четыре участка,  три из которых выполнены из ферромагнитного материала ( например: электротехническая сталь Э2 ),  кривая  намагничивания  которого  известна рис. 1.9. Четвёртый участок – воздушный зазор.

 

 

Характерный признак неразветвлённой магнитной цепи – магнитный поток Ф на всех участках один и тот же (рис. 1.8). Его значение задано в условии задачи. Магнитный поток Ф называется основным. Этот поток замыкается по магнитопроводу в отличие от потока рассеяния Фр, силовые линии которого замыкаются вокруг витков катушки по воздуху. Обычно Ф значительно больше Фр.

Магнитная проницаемость воздуха m0=4p×10-7 Гн/м ничтожно мала по сравнению с проницаемостью ферромагнитного магнитопровода и магнитное сопротивление потоку Фр несравненно выше, чем для потока Ф (Фр<<Ф).

Чтобы использовать при расчете закон полного тока, выберем контур интегрирования, проходящий внутри катушки с числом витков w и совпадающий со средней линией магнитной индукции. Разобьем магнитную цепь на отдельные участки: участок da – длина средней линии магнитной индукции l1, площадь поперечного сечения S1, на участке ab длина l2, площадь поперечного сечения S2 , на участке cd длина l3 , площадь поперечного сечения S3 , на участке воздушного зазора длина l0 , площадь S0=S2.

Пусть S1> S0=S2> S3 , тогда магнитная индукция по участкам:

Учитывая соотношения между площадями сечений, получим B1<B2=B0<B3. Далее по кривой намагничивания рис. 1.9, определим напряжённость магнитного поля на ферромагнитных участках Н1 ,H2, Н3.

Напряженность поля в зазоре рассчитывается по формуле: ,где =4p×10-7 Гн/м – магнитная постоянная.

Так как напряженность поля на каждом из четырех участков постоянна, интегральная формула закона полного тока принимает следующий вид: 1.8.

Из этого уравнения определяется МДС w×I. Отметим, что в уравнении 1.8 слева – сумма падений магнитных напряжений на участках магнитной цепи. Уравнение 1.8 можно представить иначе, если заменить магнитные напряжения в левой части уравнения произведениями потока Ф на магнитные сопротивления участков магнитной цепи (формула 1.6) и общий для всех участков поток Ф вынести за скобки, тогда

, откуда 1.9.

где .

Абсолютная магнитная проницаемость m1 , m2 и m3 определяются с помощью кривой намагничивания рис. 1.9

Выражение 1.9 как и формулу 1.6 называют законом Ома для магнитной цепи.

 

6.4.1.2. Прямая задача при расчете разветвленных цепей.

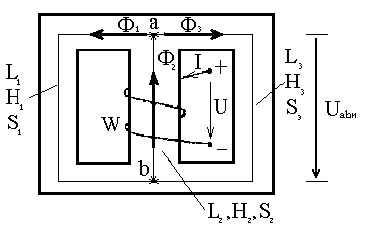
6.4.1.2.а Симметричная магнитная цепь.(рис. 1.10)

 

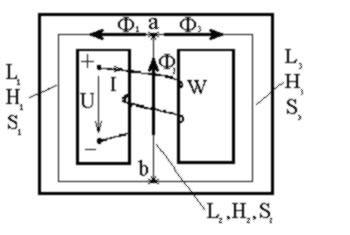
рис.1.10.

В этой цепи l1=l3 и S1=S3. Трехстержневой магнитопровод изготовлен из однородного ферромагнитного материала (кривая намагничивания известна). Магнитные сопротивления стержней 1 и 3 одинаковы. Поток Ф2, возникающий в среднем стержне, разделяется в т. а на две равные части Ф1=Ф3=Ф2 /2.

Пусть задано значение магнитного потока Ф3, требуется определить МДС w×I намагничивающей обмотки.

Структуру решения можно представить так:  и Н2 определяют по кривой намагничивания. МДС можно определить из уравнения:  wI = H3l3 + H2l2.

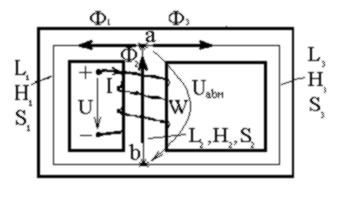
6.4.1.2.б Несимметричная магнитная цепь.(рис. 1.11).

 

рис.1.11

Здесь S1=S3 и l3=2l1. Задан поток Ф3, определить МДС w×I.

Схема решения:  по кривой намагничивания, тогда магнитное напряжение

– по кривой намагничивания, затем Ф1=B1S1 ,  Ф2=Ф1+Ф3   , H2 – по кривой намагничивания. МДС w×I определим из уравнения

w×I = H3l3 + H2l2=Н1l1 + H2l2 .

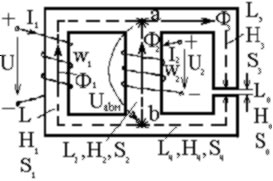
6.4.1.2.в Несимметричная магнитная цепь с двумя намагничивающими обмотками.(рис.1.12).

 

рис.1.12.

 

Расчет подобных магнитных цепей производят, используя законы Кирхгофа для магнитных цепей. Перед записью уравнений произвольно намечают направления потоков в стержнях (Ф1 , Ф2 и Ф3) и выбирают направления обхода контуров. На рис. 1.12 направления потоков Ф1 и Ф2 приняты совпадающими с МДС w1I1 и w2I2.

Условимся со знаком «+» записывать потоки, направленные к узлу а, иначе – со знаком «-».

Со знаком «+» записывать магнитные напряжения, если направление потока на участке цепи совпадет с направлением обхода контура, иначе – со знаком «-».

Со знаком «+» записывать МДС, положительное направление которых совпадает с направлением обхода, иначе – со знаком «-».

Для цепи (рис. 1.12) можно записать следующие уравнения по законам Кирхгофа:

1.10
1.11
1.12

примечание: вместо одного из двух последних уравнений можно записать уравнение для левого контура:

Пусть требуется определить МДС w2I2, чтобы магнитная индукция в воздушном зазоре третьего стержня имела заданное значение В0.

Решение:

S0=S3, имеем В3=В0, тогда поток Ф3=В3S3=В0 S0

По кривой намагничивания определим напряженность Н3

В4=Ф3 / S4 и по кривой намагничивания определим Н4

Напряженность поля в зазоре Н0=В0/m0

Из уравнения 1.12 определим напряженность Н2 и по кривой намагничивания находим В2 и поток Ф2=В2S2

Из уравнения 1.10 определяется поток Ф1=Ф3 – Ф2

Находим индукцию В1=Ф1/ S1 и далее Н1 – по кривой намагничивания

Искомое значение w1I1 получаем из уравнения 1.11

 

6.4.2. Решение обратной задачи.

6.4.2.1. Неразветвленная магнитная цепь.(рис. 1.8)

Задано значение МДС w×I, требуется определить магнитный поток Ф. Если известно, что магнитная цепь устройства в рабочих режимах не насыщена и можно считать магнитную проницаемость ферромагнитных участков , то, подсчитав магнитные сопротивления участков цепи можно определить поток Ф из закона Ома для магнитной цепи: В общем же случае принимается следующий порядок решения:

2.1.1. Задаются рядом значений потока Ф (Ф’, Ф’’ и т.д.), по которым каждый раз определяется МДС wI (wI’, wI’’ и т.д. ), т.е. несколько раз решается прямая задача.

2.1.2. Строится вспомогательная магнитная характеристика Ф(wI)  рис. 1.17.

 

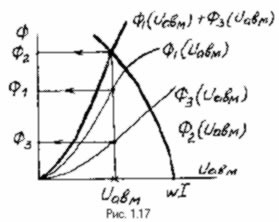2.1.3. Используя построенную характеристику, по заданному значению МДС wIзадан. определяем искомое значение потока Фиск.

 Примечание: учитывая, что для расчета нужна только часть характеристики в окрестности Фиск, рекомендуется вначале найти приближенное значение Фиск с помощью уравнения (т. к. Н0 >> H1 , Н2 и Н3),

из которого определяется напряженность поля в зазоре Н0 и далее  –   В0 = m0S0 и приближенное значение потока Фиск=В0S0 , и далее выполняются 2.1.1 – 2.1.3  пункты расчета.

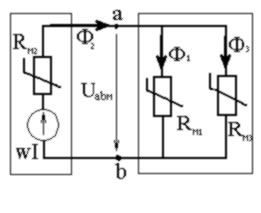
6.4.2.2. Разветвленная несимметричная магнитная цепь.(рис.1.14).

 

рис.1.14

По заданному значению МДС w×I определить магнитные потоки Ф1 , Ф3 , Ф2 .

Магнитные сопротивления отдельных участков магнитопровода в общем случае нелинейные из–за нелинейной зависимости между магнитными потоками и током намагничивающей обмотки Ф(I).

При решении задачи удобнее использовать схему замещения (рис. 1.15) магнитной цепи (рис. 1.14), подобную схеме нелинейной электрической цепи постоянного тока с той разницей, что ЭДС заменена на МДС w×I, токи в ветвях электрической цепи – потоками Ф1, Ф2 , Ф3 в ветвях магнитной цепи, нелинейные сопротивления R(I) – магнитными сопротивлениями RM(Ф).

 

 

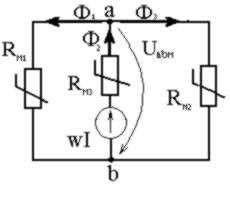рис.1.15

Выделим ветвь с МДС w×I в активный двухполюсник. Второй двухполюсник, в составе которого две параллельные ветви с нелинейными магнитными сопротивлениями RM1 и RM3 – пассивный (рис. 1.16).

 

рис.1.16

Задача решается графоаналитическим методом.

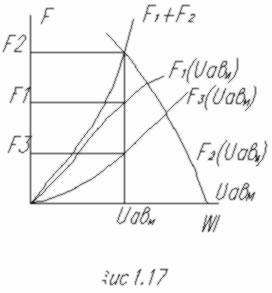
Вебер-амперная характеристика активного двухполюсника  строится в соответствии с уравнением второго закона Кирхгофа для магнитной цепи:

1.13

Для ее построения задаемся рядом значений потока Ф2 , определяем ряд значений индукции , и по кривой намагничивания каждый раз находим напряженность магнитного поля Н2; далее по уравнению 1.13 подсчитываем соответствующие значения магнитных напряжений UabM и строим вебер-амперную характеристику активного двухполюсника Ф2(UabM)  рис. 1.17.

 

рис.1.17

Чтобы получить вебер-амперную характеристику пассивного двухполюсника, нужно сначала построить характеристики Ф1(UabM) и  Ф3(UabM) по описанной выше методике с использованием зависимостей:

1.14
1.15

Так как ветви с потоками Ф1 , Ф3 соединены между собой параллельно и , то для построения характеристики пассивного двухполюсника Ф1(UabM)+ Ф3(UabM) складываем ординаты характеристик ветвей при одних и тех же значениях UabM.

Поскольку двухполюсники соединены последовательно (рис. 1.16), то точка пересечения их вебер – амперных характеристик определит общий для обоих магнитный поток Ф2 и магнитное напряжение UabM.

Располагая значением UabM  и вебер – амперными характеристиками Ф1(UabM) и Ф3(UabM) определяем по рис. 1.17 значения потоков Ф1 и Ф3.

↑ Вверх, к содержанию раздела ↑

6.5. Расчет силы притяжения электромагнита.

Электромагниты в технических устройствах применяются для подъема грузов, переключения контактов реле магнитных пускателей, вентилей гидравлических систем, растормаживания механических тормозов и т. д.

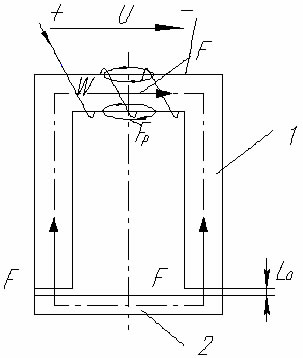
На рис. 1.18 представлена схема магнитной цепи электромагнита.

 

рис.1.18

Подвижная часть (якорь – 2, рис. 1.18) магнитопровода электромагнита отделена от его неподвижной части 1 рис. 1.18 воздушным зазором. При подключении намагничивающей обмотки к источнику электрической энергии возбуждается магнитное поле, возникает электромагнитная сила, действующая на якорь, и он, преодолевая силу тяжести, действие пружин и т. п., притягивается к неподвижной части магнитопровода.

Расчет силы притяжения электромагнита часто проводится приближенно, исходя из следующих соображений:
1. Ток I в обмотке имеет установившееся значение.

2. Сердечник 1 и якорь 2 не насыщены.

3. Потоком рассеяния Фр и выпучиванием магнитного поля в зазорах пренебрегают.

4. При изменении воздушного зазора на dl0 магнитная индукция В0 остается постоянной.

В таком случае можно считать, что механическая работа по перемещению якоря в направлении действия сил F на расстояние dl0 равна изменению энергии магнитного поля в воздушных зазорах, вследствие уменьшения их объемов.

С учетом двух воздушных зазоров имеем:

механическая работа.
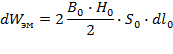энергия магнитного поля в двух зазорах длиной dl0, где – плотность электромагнитной энергии (энергия в единице объема зазора), S0 – площадь одного воздушного зазора. Приравняв dWмех и dWэм, получим расчетную формулу силы притягивания электромагнита 1.16.

↑ Вверх, к содержанию раздела ↑

 

6.6. Об индуктивности намагничивающей обмотки.

Если катушка не имеет ферромагнитного сердечника, то зависимость потокосцепления y от тока катушки I линейная и индуктивность катушки

. Здесь индуктивность, как коэффициент пропорциональности между потокосцеплением и током катушки, является линейным параметром катушки. То же замечание относится и к намагничивающим обмоткам с ненасыщенным магнитопроводом( ).

Если поток Ф сцепляется со всеми w витками катушки (обмотки), то потокосцепление     , где , тогда индуктивность

  1.17.

Здесь – магнитное сопротивление на пути магнитного потока.

Абсолютная магнитная проницаемость ненасыщенных ферромагнитных материалов mа >> m0  – магнитной проницаемости вакуума (4p×10-7 Гн/м). Поэтому размещение намагничивающей  обмотки на ферромагнитном магнитопроводе резко увеличивает индуктивность катушки.

Физически последнее утверждение объясняется способностью ферромагнетиков усиливать внешнее магнитное поле, созданное током обмотки, за счет ориентации по направлению поля собственных областей самопроизвольного намагничивания. Эта ориентация выражена тем четче, чем больше ток обмотки. Когда все области самопроизвольного намагничивания ориентируются в направлении внешнего поля, наступает магнитное насыщение магнитопровода, его магнитная проницаемость и индуктивность обмотки резко снижаются, магнитопровод перестает выполнять функцию локализации магнитного поля.

В общем случае, когда приходится считаться с тем что , используется понятие дифференциальной индуктивности  (индуктивность L становится нелинейным параметром обмотки).

Индуктивность, как элемент схемы замещения реальной электрической цепи, дает возможность учитывать при расчетах явление самоидукции (при переменных токах катушки) и явление накопления энергии в магнитном поле катушки.

↑ Вверх, к содержанию раздела ↑