Глава 2. Электрические цепи однофазного синусоидального тока.
Содержание главы:
- 2.1. Синусоидальный ток и основные характеризующие его величины
- 2.2. Среднее и действующее значение синусоидального тока и ЭДС
- 2.3. Сложение синусоидальных функций времени. Векторные диаграммы. Основы символического метода расчета
- 2.4. Пассивные элементы электрической цепи
- 2.5. Резистивный элемент
- 2.6. Индуктивный элемент в цепи синусоидального тока
- 2.7. Емкостный элемент в цепи синусоидального тока
- 2.8. Последовательное соединение элементов r, L, C
- 2.9. Параллельное соединение элементов r, L, C
- 2.9.1. Мощность в цепи синусоидального тока. Комплексная мощность
- 2.10. Законы Кирхгофа и уравнение энергетического баланса в комплексной форме
- 2.11. Резонанс в цепях синусоидального тока
- 2.11.1. Резонанс напряжений
- 2.11.2. Резонанс токов
- 2.12. Резонанс напряжений и токов в разветвленных цепях
2.1. Синусоидальный ток и основные характеризующие его величины.
Синусоидальным током называют ток, изменяющийся во времени по синусоидальному закону (рис. 2.1):
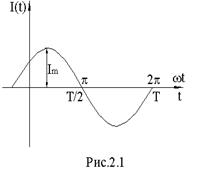
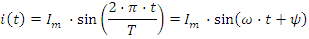
Ток i(t) называют мгновенным. Максимальное значение тока называют амплитудой и обозначают Im. Период T- это время, за которое совершается одно полное колебание. Частота равна числу колебаний в секунду f=1/T [Гц].
Угловая частота ω=2⋅π⋅f=2⋅π/T. Аргумент синуса, т.е. (ω⋅t+ψ), называеться фазой. Фаза характеризует состояние колебания в данный момент времени t. Начальная фаза тока-ψ.
Любая синусоидальная функция характеризуется тремя величинами: амплитудой, угловой частотой и начальной фазой. Синусоидальные токи и ЭДС сравнительно низких частот, до нескольких килогерц, получают с помощью синхронных генераторов (их изучают в курсе электрических машин). Синусоидальные токи и ЭДС высоких частот получают с помощью ламповых и полупроводниковых генераторов, подробно рассматриваемых в разделе – электроника.
2.2. Среднее и действующее значение синусоидального тока и ЭДС.
Принято среднее значение функции времени определять за период:
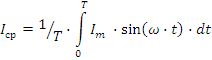
Для синусоидальной функции среднее значение за период равно нулю. Используется также понятие среднего значения синусоидальной функций за полпериода:
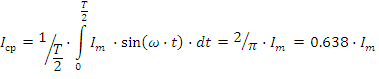
Действующим значением синусоидальной функции называется ее среднеквадратичное значение за период:
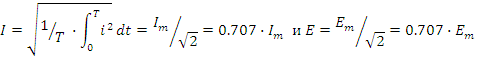
Большинство измерительных приборов амперметров и вольтметров показывают действующее значение измеряемой величины.
2.3. Сложение синусоидальных функций времени. Векторные диаграммы. Основы символического метода расчета.
Пусть требуется сложить два тока:
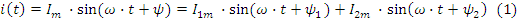
Тригонометрическому уравнению (1) можно дать геометрическую интерпретацию, если каждому синусоидальному значению поставить в соответствие вектор на плоскости в координатах X,Y (рис. 2.2):
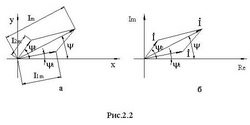
Длиной вектора будет амплитуда тока, а фазой – начальная фаза синусоиды- ψk.
Совокупность векторов, соответствующая уравнениям для токов или напряжений, называется векторной диаграммой. Уравнению (1) можно поставить в соответствие другое уравнение, в котором каждая синусоида будет представлена в виде комплексного числа. Ток
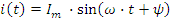
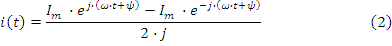
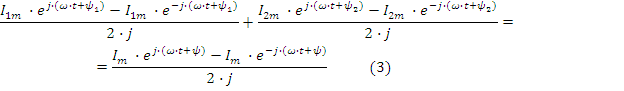
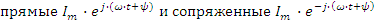
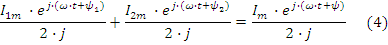
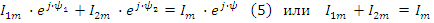
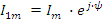 называется током в комплексной форме или комплексом тока по максимальному значению. Здесь Im модуль комплекса по максимальному значению, а ψ фаза комплекса. Если за модуль комплекса принять не амплитудное, а действующее значение, то получим комплекс по действующим значениям I=I⋅ej⋅ψ или просто комплекс тока.
называется током в комплексной форме или комплексом тока по максимальному значению. Здесь Im модуль комплекса по максимальному значению, а ψ фаза комплекса. Если за модуль комплекса принять не амплитудное, а действующее значение, то получим комплекс по действующим значениям I=I⋅ej⋅ψ или просто комплекс тока.
Уравнение (5) для комплексов тока примет вид:
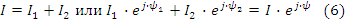
2.4. Пассивные элементы электрической цепи.
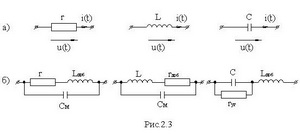
Резистор, индуктивность и емкость являются пассивными элементами электрической цепи. Резистор r или активное сопротивление цепи – это элемент, в котором происходит рассеивание энергии в виде тепла или превращение электрической энергии в другой вид энергии: световую, химическую или механическую. Индуктивность L и емкость C называются реактивными элементами цепи, в них происходят накапливание энергии в виде магнитного или электрического поля; рассеивание энергии в таких элементах отсутствует. Идеальные элементы r,L,C на схеме обозначаются так, как это показано на рис. 2.3а.Б.
Реальные катушки индуктивности и конденсаторы рассеивают часть энергии - этот факт учитывается с помощью добавочных сопротивлений rK для катушки и rутечки для кондесаторов рис. 2.3б. В проволочных сопротивлениях и катушках индуктивности учитывают также межвитковую емкость CM рис.2.3б.; в реальном конденсаторе можно учесть паразитную индуктивность подводящих контактов Lдоб, рис.2.3б.
Рассматривая пассивные элементы цепи r, L, C ответим на следующие вопросы:
- Каково соотношение между мгновенным значением тока и напряжения на каждом элементе? Каков вид векторов тока и напряжения?
- Какова мгновенная мощность p(t) и накопленная энергия магнитного или электрического полей?
- Каково соотношение тока и напряжения на элементе в комплексной форме, как изображаются вектора тока и напряжения на комплексной плоскости?
Под мгновенным значением мощности p(t) понимают произведение мгновенного значения напряжения u(t) на элементе цепи на мгновенное значение протекающего по элементу тока i(t):
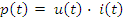
2.5. Резистивный элемент.
Пусть ток в резисторе:
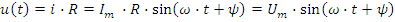
Мгновенное значение напряжения на резисторе:

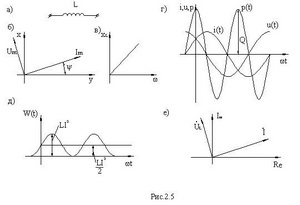
Векторы тока и напряжения на резисторе приведены на рис.2.4б:
Закон Ома для резистора имеет вид: Im=Um/R
Пусть м гновенная мощность p(t) равна:
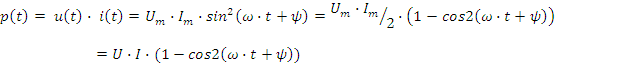
В комплексной форме напряжение на резисторе записывается в виде:
2.6. Индуктивный элемент в цепи синусоидального тока.
Индуктивный элемент учитывает явления накапливания энергии магнитного поля и характеризуется зависимостью потокосцепления ψ от тока i:
Мгновенное значение напряжения на индуктивности:
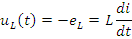
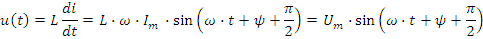
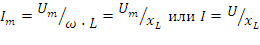
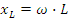 - индуктивное сопротивление катушки, измеряется в Омах (Ом).
- индуктивное сопротивление катушки, измеряется в Омах (Ом).
Сопротивление xL - частотно зависимая величина, увеличивается с ростом частоты, рис. 2.5в.
Мгновенная мощность:
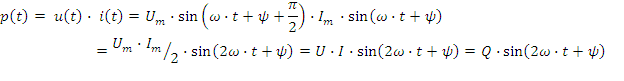
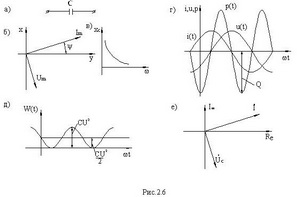
Мощность 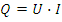 называется реактивной и измеряется в вольт-амперах реактивных (ВАр). Временные диаграммы i(t),u(t),p(t) для катушки приведены на рис.2.5г. Средняя мощность равна нулю, т.е. рассеивание мощности или потери отсутствуют. Энергия магнитного поля катушки равна:
называется реактивной и измеряется в вольт-амперах реактивных (ВАр). Временные диаграммы i(t),u(t),p(t) для катушки приведены на рис.2.5г. Средняя мощность равна нулю, т.е. рассеивание мощности или потери отсутствуют. Энергия магнитного поля катушки равна:
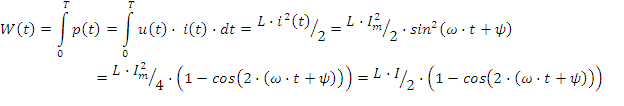
Временная диаграмма W(t), приведена на рис.2.5д. Максимальная энергия магнитного поля катушки:
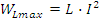
Так как напряжение на катушке:

то
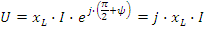
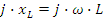 - индуктивное сопротивление в комплексной форме. Оператор
- индуктивное сопротивление в комплексной форме. Оператор 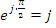 отражает дифференцирование тока в формуле напряжения на индуктивности. Закон Ома в комплексной форме:
отражает дифференцирование тока в формуле напряжения на индуктивности. Закон Ома в комплексной форме:
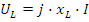
2.7. Емкостный элемент в цепи синусоидального тока.
Емкость отражает явление накапливания энергии электрического поля и характеризуется зависимостью заряда q от напряжения: 
Мгновенное значение напряжения на конденсаторе:
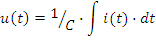
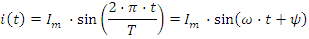
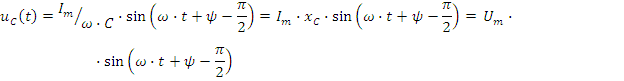
Это напряжение отстает от тока на угол π/2. Векторы тока и напряжения приведены на рис.2.6 б.
Закон Ома для емкости:
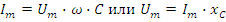
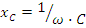 - емкостное сопротивление, измеряется в омах (Ом). Емкостное сопротивление уменьшается с ростом частоты. Зависимость XC от частоты приведена на рис.2.6в.
Мгновенная мощность на конденсаторе:
- емкостное сопротивление, измеряется в омах (Ом). Емкостное сопротивление уменьшается с ростом частоты. Зависимость XC от частоты приведена на рис.2.6в.
Мгновенная мощность на конденсаторе:

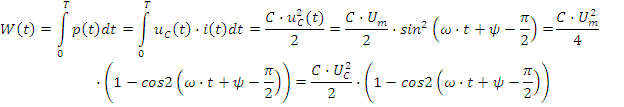
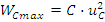
Так как:
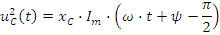
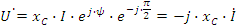
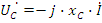
Векторы ÚC и Í приведены на рис. 2.5е.
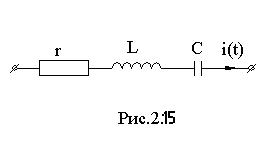
2.8. Последовательное соединение элементов r, L, C.
Для схемы рис.2.7 уравнение по второму закону Кирхгофа для мгновенных значений запишем в виде:
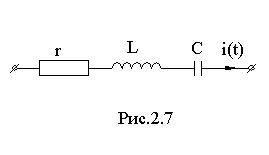
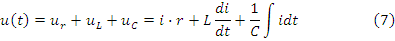
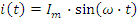
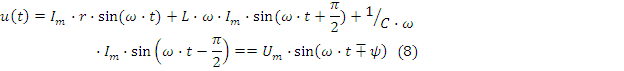
Вектор тока и векторная диаграмма напряжений приведены на рис.2.8 Векторы напряжений на активном и реактивном элементах ортогональны, а векторы напряжений на L и C смещены на π
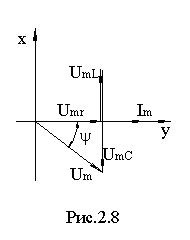
В комплексной форме уравнение (8) примет вид:
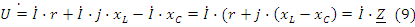

На комплексной плоскости сопротивления r, j⋅xL, -j⋅xC, Z – образуют треугольник сопротивления, рис. 2.9.
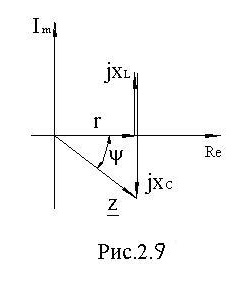
Если сопротивления умножить на Í, получим диаграмму напряжений, рис. 2.10.
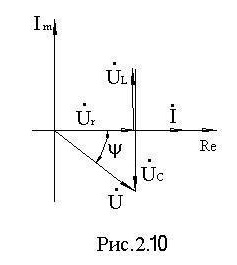
Сравнивая уравнения (8) и (9), отметим, что дифференциальные уравнения (8) после замены мгновенных значений их комплексными символами переводится в уравнение алгебраическое (9). Это одно из преимуществ комплексного метода расчета.Введение понятия комплексного сопротивления, позволяет написать закон Ома для всей цепи в комплексной форме:
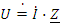
Таким образом, для целей переменного тока можно составлять уравнения, по структуре сходной с уравнениями для цепей постоянного тока. В современных условиях контроль над технологическими процессами, потреблением электрической энергии, режимом работы электрооборудования, измерением неэлектрических величин осуществляется с помощью электроизмерительных приборов. Эти приборы измеряют ток, напряжение, мощность, частоту, электрическую энергию и т.д.
2.9. Параллельное соединение элементов r, L, C.
Для схемы рис.2.11 составим уравнение по первому закону Кирхгофа для мгновенных значений:
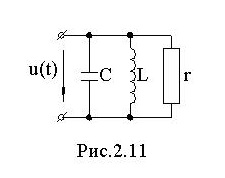
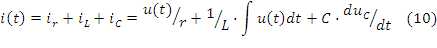
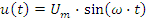
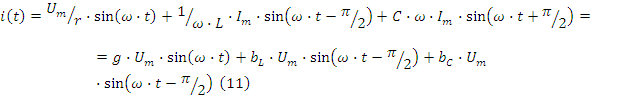

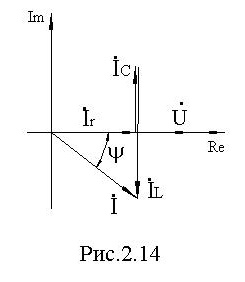
Единица измерения проводимостей - сименс (Сим). Векторная диаграмма токов приведена на рис. 2.12.
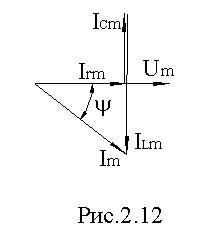
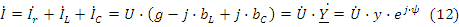

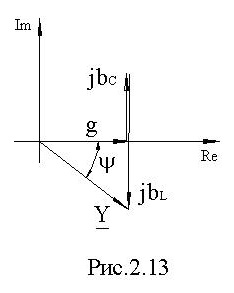
Проводимости g, -j⋅bL, j⋅xC, Y образуют треугольник проводимости, рис. 2.13.
Комплексная векторная диаграмма токов для уравнения (12) приведена на рис. 2.14.
2.9.1. Мощность в цепи синусоидального тока. Комплексная мощность.
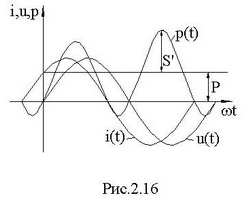
Пусть в цепи (рис. 2.15) ток равен
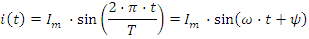

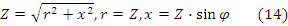
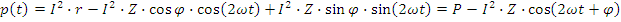
Временные диаграммы i(t),u(t),p(t) приведены на рис. 2.16.
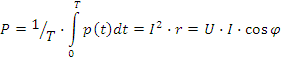
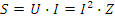
называется полной мощностью, измеряется в вольт-амперах. Мощности P и S связаны по закону треугольника мощностей, рис. 2.17.

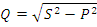
Пример.
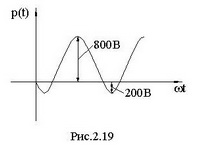
График мгновенной мощности приведен на рис. 2.19.
Решение:
Размах значений мощности 1000 ВА, амплитудное значение 500ВА, это полная мощность S. Среднее значение мощности:
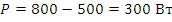
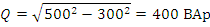
Отношение активной мощности к полной, (рис.2.17) равное косинусу угла сдвига фаз между напряжением и током, называется коэффициентом мощности:
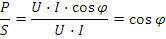
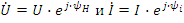
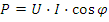
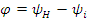 Отсюда следует, что при определении комплекса мощности фаза тока должна быть взята с обратным знаком, т.е. комплекс тока должен быть заменен на сопряженный. Полная комплексная мощность:
Отсюда следует, что при определении комплекса мощности фаза тока должна быть взята с обратным знаком, т.е. комплекс тока должен быть заменен на сопряженный. Полная комплексная мощность:
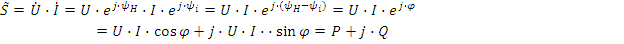
2.10. Законы Кирхгофа и уравнение энергетического баланса в комплексной форме.
Первый закон Кирхгофа: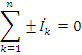
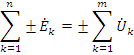
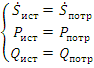
2.11. Резонанс в цепях синусоидального тока.
Реактивные сопротивления и проводимость являются частотно-зависимыми величинами. Следовательно, при последовательном или параллельном соединении элементов L и C возможна на какой-то частоте полная компенсация реактивных сопротивлений или проводимостей. Режим, при котором наступает компенсация, называют резонансом. При резонансе входное сопротивление цепи становится активным, входное напряжение совпадает по фазе с входным током, а полная мощность будет активной. Угловая частота, ω0, при которой наступает резонанс, называется резонансной или собственной угловой частотой цепи. Различают две разновидности резонанса: резонанс напряжений и резонанс токов.
2.11.1. Резонанс напряжений.
Может возникнуть в цепи с последовательным соединением L и C рис. 2.20а.
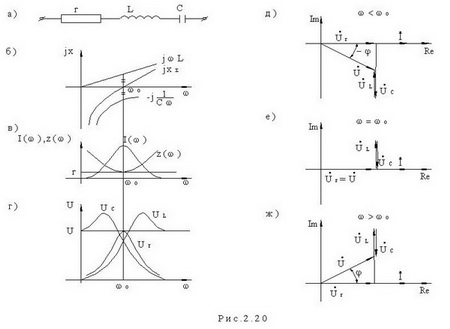
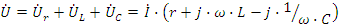
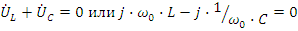
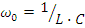 . Настройку цепи в резонанс, изменение параметров цепи при частотах, отличных от резонансной можно увидеть, если построить частотные характеристики сопротивлений, тока в цепи и напряжений на r,L,C.
На рис. 2.20б, в, г приведены частотные характеристики реактивных сопротивлений
. Настройку цепи в резонанс, изменение параметров цепи при частотах, отличных от резонансной можно увидеть, если построить частотные характеристики сопротивлений, тока в цепи и напряжений на r,L,C.
На рис. 2.20б, в, г приведены частотные характеристики реактивных сопротивлений
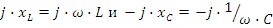
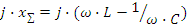
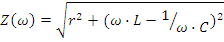
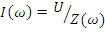
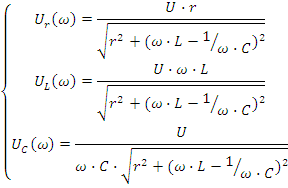
По графику j⋅xΣ(ω) определена резонансная частота ω0, по графику Z(ω) можно увидеть, что сопротивление цепи при резонансе минимально и равно активному сопротивлению, по графику I(ω) - что ток в цепи при резонансе максимален. Графики Ur(ω), UL(ω), UC(ω) имеют ярко выраженный избирательный характер, т.е. имеют максимальные значения на резонансной частоте или вблизи нее. Можно также отметить, что напряжения UC, UL при резонансе могут превышать значение входного напряжения. Это хорошо иллюстрируется с помощью векторных диаграмм напряжения приведенных на рис.2.20д, е, ж при частотах ω≤ω0, ω=ω0 и ω≥ω0. Обратите также внимание на значения угла φ на этих частотах и сопоставьте эти значения с характером реактивных сопротивлений на соответствующих частотах. При частотах ω≤ω0, реактивное сопротивление носит емкостной характер и cos(φ)≤0.
2.11.2. Резонанс токов.
Может возникнуть в цепи с параллельным соединением L и C рис. 2.21а.

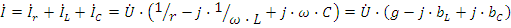
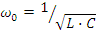
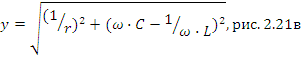
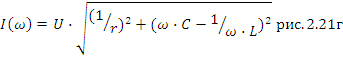
Здесь отмечена резонансная частота, полная проводимость цепи при резонансе минимальна и полный ток минимален. Векторные диаграммы токов, построенные для частот ω≤ω0, ω=ω0 и ω≥ω0 рис. 2.21е, д, ж, позволяют убедиться, что токи в катушке и конденсаторе могут значительно превышать полный ток.
2.12. Резонанс напряжений и токов в разветвленных цепях.
Мы рассмотрели резонанс в последовательном и параллельном контурах с идеальными элементами L и C. Рассмотрим другие более сложные примеры. Для цепи рис. 2.22 запишем условие резонанса, определим резонансную частоту и ток в цепи.
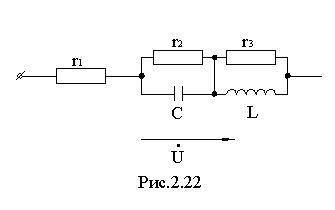
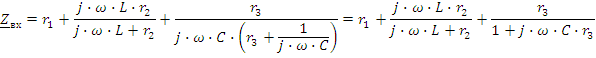
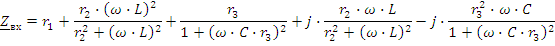
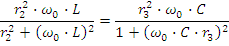
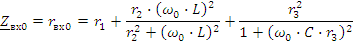
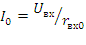
Для цепи, приведенной на рис.2.23 , возможен резонанс токов. Запишем входную проводимость цепи:
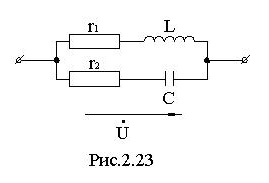
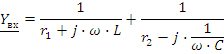
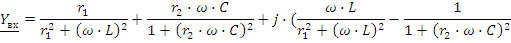
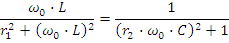
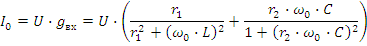
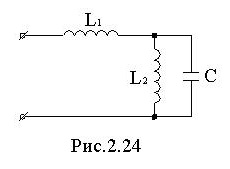
В разветвленных цепях с L и C возможны несколько резонансов. Так в цепи рис. 2.24 возможны и резонанс токов в ветвях L,C и резонанс напряжений для всей цепи.