Прикладная математика 

1. математический анализ,

2. дифференциальные уравнения,

3. алгебра и геометрия,

4. функциональный анализ,

5. комплексный анализ,

6. теория устойчивости,

7. дискретная математика: булевы функции, исчисления высказываний, теория графов,

8. теория чисел,

9. дифференциальная геометрия и топология,

10. вычислительная математика: численные методы решения задач линейной алгебры и дифференциальных уравнений, методы оптимизации, теория разностных схем.

11. теории вероятностей, математическая статистика и случайные процессы,

12. исследование операций.

Также проводится подготовка слушателей по следующим дисциплинам:

1. операционные системы и сети,

2. программирование,

3. компьютерная графика,

4. базы данных.

В процессе обучения общетеоретические знания подкрепляются математическим моделированием конкретных технических систем. В обучении широко используется компьютерная техника и информационные технологии. В рамках указанного направления подготовки осуществляется специализация по математической теории процессов управления техническими системами. Для чтения специальных курсов приглашаются преподаватели факультета Вычислительной математики и кибернетики МГУ им. М.В. Ломоносова, ведущие сотрудники Института проблем управления РАН, Института системного анализа РАН.

Наши выпускники хорошо владеют математическим аппаратом и умеют строить математические модели различных технических систем, исследовать эти модели аналитическими и численными методами, а также выдавать рекомендации по совершенствованию технических систем на основе проведенного анализа. Дипломные работы, как правило, посвящены разработке моделей нелинейных процессов в технических системах с управлением и разработке новых методов и алгоритмов управления. Также много работ связано с применением методов стохастического анализа и с решением различных систем дифференциальных уравнений в частных производных. Тематика дипломных работ разнообразна и включает:

·       Управление самолѐтом вертикального взлѐта и посадки на этапах взлѐта и прямолинейного разгона.

·       Оптимизация параметров алгоритма переориентации космического аппарата на основе концепции обратной задачи динамики.

·       Робастная стабилизация двухзвенного робота - манипулятора.

·       Управление плоским перемещением пятизвенного двуногого робота.

·       Управление торможением автомобиля с использованием наблюдателя состояния.

·       Формулы Фейнмана для параболического уравнения второго порядка и их применение.

·       Математическое моделирование пространственно - временной динамики численности сообществ фито и зоопланктона с учетом аллелопатии.

·       Математическое моделирование процессов формирования

·       температурных полей охлаждаемой стенки при концентрированных внешних тепловых воздействиях

·       Описание и прогнозирование экономических временных рядов статистическими методами.

Продолжительность обучения 2.5 года.

Выпускники кафедры работают в НИИ и КБ, разрабатывающих новую технику, а также в коммерческих фирмах, связанных с информационными технологиями. Сотрудниками кафедры, совместно со студентами, разработана и реализована система управления перемещением мобильного робота из стартовой точки в заданную конечную точку по полигону с препятствиями.

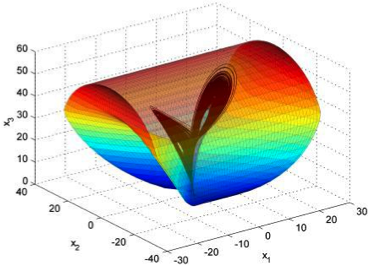
Синтезирована система управления продольным движением летательного аппарата.

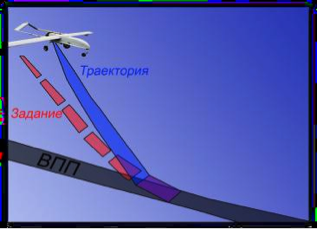
А также проведены автоматические расчеты траектории движения БПЛА в режиме реального времени.