|
|
|||
|
|||
|
ГЛАВА 5
5.7. Каноническое распределение Гиббса |
|
Наиболее полное статистическое описание равновесного состояния может быть получено с использованием метода статистических ансамблей, предложенного в 1901 году американским физиком-теоретиком Джозайя Уиллардом Гиббсом (1839 - 1903). Здесь мы дадим только самые общие представления об этом методе.
При статистическом описании динамической системы применяется вероятностная трактовка происходящих в ней процессов. В соответствии с методом Гиббса вводится в рассмотрение большая совокупность динамических систем, находящихся в макроскопически тождественных состояниях, то есть имеющих одинаковые значения макроскопических внутренних и внешних параметров. При этом микроскопические параметры систем различны. Такая совокупность называется статистическим ансамблем.
Пусть динамическая система представляет собой систему из
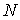 одинаковых, взаимодействующих между собой частиц. В классической динамике состояние каждой из частиц системы характеризуется значениями её радиус-вектора одинаковых, взаимодействующих между собой частиц. В классической динамике состояние каждой из частиц системы характеризуется значениями её радиус-вектора 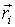 и импульса и импульса 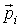 . Полная совокупность радиус-векторов . Полная совокупность радиус-векторов 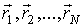 и импульсов и импульсов 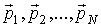 всех частиц системы описывает состояние динамической системы в целом. всех частиц системы описывает состояние динамической системы в целом.Динамика консервативной системы описывается уравнениями Гамильтона
где:
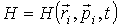 - функция Гамильтона системы, - функция Гамильтона системы, 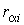 и и 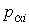 - значения проекций радиус-вектора - значения проекций радиус-вектора 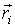 и импульса и импульса 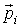 на оси декартовой системы координат, на оси декартовой системы координат, 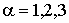 . .Если макроскопическая система представляет собой газ, частицы которого не имеют внутренней структуры и их взаимодействие между собой описывается потенциальными функциями вида:
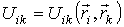 , где , где 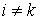 , то функция Гамильтона равна сумме кинетических и потенциальных энергий всех частиц и имеет форму: , то функция Гамильтона равна сумме кинетических и потенциальных энергий всех частиц и имеет форму:
Здесь:
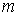 - масса частицы газа. - масса частицы газа.Рассмотрим замкнутую динамическую систему, находящуюся в тепловом контакте с термостатом, имеющим температуру
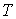 . Для такой системы функция Гамильтона явным образом не зависит от времени: . Для такой системы функция Гамильтона явным образом не зависит от времени: 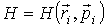 . Микроскопическое состояние системы задается совокупностью координат . Микроскопическое состояние системы задается совокупностью координат 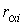 и импульсов и импульсов 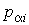 в 6N-мерном пространстве в 6N-мерном пространстве 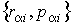 , получившем название фазового пространства. Объем, который занимает система в этом пространстве, обозначим как , получившем название фазового пространства. Объем, который занимает система в этом пространстве, обозначим как 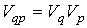 , где , где 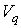 и и 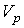 - объемы координатного и импульсного пространств соответственно. - объемы координатного и импульсного пространств соответственно.Совокупность термодинамически тождественных систем с заданным числом частиц
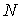 и физическим объемом и физическим объемом 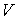 , находящихся в контакте с термостатом называется каноническим ансамблем Гиббса. Для этого ансамбля может быть введено каноническое распределение Гиббса, имеющее вид: , находящихся в контакте с термостатом называется каноническим ансамблем Гиббса. Для этого ансамбля может быть введено каноническое распределение Гиббса, имеющее вид:
где величина
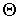 определяется из условия нормировки (5.5): определяется из условия нормировки (5.5):
Здесь:
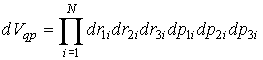 - элементарный объем фазового пространства. - элементарный объем фазового пространства.С помощью канонического распределения Гиббса может быть решена задача определения наблюдаемых макроскопических параметров любой системы, находящейся в термодинамическом равновесии с термостатом и имеющей неизменное число частиц. Но непосредственное применение распределения Гиббса для определения макроскопических параметров системы связано с интегрированием 6N-мерной функции распределения, что представляется достаточно затруднительным для реальной системы, состоящей из достаточно большего количества частиц. Поэтому для решения многих прикладных задач возможно использование более простых функций распределения. Примером такой функции является распределение Максвелла-Больцмана, которое может быть получено из распределения Гиббса для частного случая идеального газа.
|
|
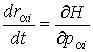 ,
,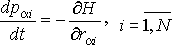 ,
,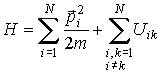 .
.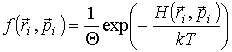 ,
,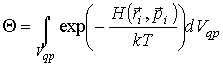 .
.