|
|
|||
|
|||
|
ГЛАВА 5
5.8. Равновесные флуктуации |
|
Проведенное в предыдущих параграфах статистическое описание равновесных состояний термодинамической системы позволяет на основе функции распределения определять средние значения макроскопических параметров её состояния. Однако в любой, даже равновесной системе, существуют случайные отклонения от этих средних значений, которые можно экспериментально наблюдать при долговременных измерениях термодинамических параметров состояния системы. Так, в частности, если длительное время и с высокой точностью измерять температуру небольшого объема газа, то можно заметить, что она претерпевает небольшие случайные изменения даже в случае отсутствия внешних тепловых возмущений. На наличие случайных изменений давления указывает возникновение хаотического движения небольших частичек, помещенных в среду, называемое броуновским движением.
Указанные отклонения от средних значений термодинамических параметров состояния системы называются флуктуациями. Они возникают вследствие хаотического теплового движения частиц термодинамической системы. Мы будем рассматривать только флуктуации в равновесной системе, которые соответственно называются равновесными флуктуациями.
Пусть равновесное состояние системы характеризуется некоторым параметром
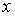 , среднее значение которого равно , среднее значение которого равно 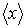 . Тогда флуктуации этого параметра определяются как отклонение его значения от среднего: . Тогда флуктуации этого параметра определяются как отклонение его значения от среднего:
Из формулы (5.89) можно сделать заключение, что среднее значение флуктуаций
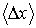 равно нулю: равно нулю:
Для количественной оценки величины флуктуаций можно использовать средний квадрат отклонения параметра от его среднего значения:
Аналогичную формулу можно записать и для среднего квадрата флуктуаций
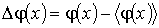 любой функции любой функции 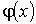 : :
Наибольшее распространение для количественной оценки флуктуаций нашла величина, равная квадратному корню из среднего квадрата
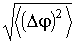 , получившая название среднеквадратичной флуктуации, а также её отношение к среднему значению: , получившая название среднеквадратичной флуктуации, а также её отношение к среднему значению: 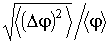 , которая называется среднеквадратичной относительной флуктуацией. , которая называется среднеквадратичной относительной флуктуацией.Отметим, что при расчете всех указанных выше средних значений может быть использована формула (5.6), позволяющая находить средние значения любых параметров термодинамической системы в случае, если известна функция распределения её динамических переменных. А как отмечалось выше, задача нахождения функции распределения для равновесного состояния термодинамической системы может быть решена в достаточно общем случае. Примерами таких функций распределений являются распределения Максвелла-Больцмана и Гиббса.
Таким образом, статистическое описание равновесных состояний дает возможность определить не только средние значения термодинамических параметров системы, но и их флуктуации.
Применим полученные выше выражения для расчета флуктуаций кинетической энергии молекулы одноатомного идеального газа. В соответствии с формулами (5.6) и (5.74) среднее значение кинетической энергии молекулы определяется формулой:
а среднее значение квадрата этой энергии имеет вид:
Тогда средний квадрат флуктуаций кинетической энергии молекулы в соответствии с формулой (5.92) равен:
Теперь рассмотрим более общий случай. Пусть на молекулу идеального газа воздействует внешнее силовое поле, и ее функция распределения описывается распределением Максвелла-Больцмана (5.79). Тогда среднее значение полной энергии молекулы приобретает вид
а среднее значение квадрата этой энергии соответственно имеет форму
Здесь
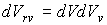 - элементарный объем в пространстве координат и скоростей. - элементарный объем в пространстве координат и скоростей.Величина
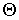 определяется из условия нормировки и имеет вид (5.80): определяется из условия нормировки и имеет вид (5.80):
Найдем производную выражения (5.98) по температуре
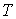 : :
Дифференцирование выражения (5.96) по температуре
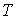 дает: дает:
или
Тогда в соответствии с равенством (5.92) имеем выражение для определения среднего квадрата флуктуаций полной энергии молекулы идеального газа во внешнем потенциальном поле:
Отметим, что записанная выше формула (5.95) является частным случаем выражения (5.102) и может быть получена из него при подстановке в его правую часть выражения (5.93) для среднего значения кинетической энергии молекулы газа.
Перейдем теперь к нахождению флуктуаций внутренней энергии идеального газа, содержащего
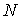 молекул и занимающего постоянный объем. Для такого газа мы можем считать, что внутренняя энергия складывается из энергий его молекул: молекул и занимающего постоянный объем. Для такого газа мы можем считать, что внутренняя энергия складывается из энергий его молекул:
Тогда среднее значение внутренней энергии равно:
а средний её квадрат соответственно определяется по формуле:
При получении формул (5.104) и (5.105) предполагалась статистическая независимость значений энергии различных молекул идеального газа. Здесь учтено также то, что рассматриваемый газ находится в равновесном состоянии, и все его молекулы имеют одинаковые значения средней энергии и её среднего квадрата.
Формулы (5.104) и (5.105) позволяют записать следующее соотношение между квадратом флуктуаций внутренней энергии всего газа и квадратом флуктуаций энергии одной молекулы:
или
Подстановка в последнюю формулу выражения (5.102) для квадрата флуктуаций энергии молекулы дает:
где учтено выражение (5.104) для среднего значения внутренней энергии газа.
Внутренняя энергия одноатомного идеального газа может быть определена по формуле (2.64) и имеет вид
где:
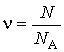 - количество молей вещества, - количество молей вещества, 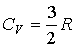 - молярная теплоемкость одноатомного газа, - молярная теплоемкость одноатомного газа, 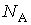 - постоянная Авогадро, - постоянная Авогадро, 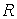 - универсальная газовая постоянная. Учитывая то, что - универсальная газовая постоянная. Учитывая то, что 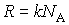 , имеем: , имеем:
С учетом этих выражений среднеквадратичную относительную флуктуацию внутренней энергии можно записать в виде:
Из этой формулы следует, что для макроскопических систем при
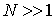 , относительные флуктуации внутренней энергии пренебрежимо малы. , относительные флуктуации внутренней энергии пренебрежимо малы.Отметим, что флуктуации в равновесном состоянии претерпевает не только внутренняя энергия, но и другие термодинамические параметры системы, такие как давление, температура, плотность, энтропия и т.д. При этом для всех этих параметров величина их относительных флуктуаций обратно пропорциональна корню из количества частиц в системе:
При этом коэффициент пропорциональности имеет величину порядка единицы. Непосредственный расчет относительных флуктуаций термодинамических параметров для равновесных состояний может быть выполнен с использованием полученных выше соотношений и выражений для термодинамических потенциалов, рассмотренных в четвертой главе.
Формулой (5.113), дающей предельно малые значения относительных флуктуаций термодинамических параметров состояния, можно пользоваться только при анализе равновесных состояний. Для состояний далеких от равновесия, например при фазовых переходах или при высокоинтенсивных внешних воздействиях на систему, флуктуации существенно возрастают, и их величины могут становиться сравнимыми со значениями самих флуктуирующих параметров. Флуктуации в таких термодинамических системах определяют характер протекания необратимых процессов, и разработка их теории является задачей неравновесной термодинамики.
Задача 5.5. Оценить величину относительных равновесных флуктуаций температуры газового термометра, содержащего один моль газа.
Решение: Один моль газа содержит число молекул, равное постоянной Авогадро:
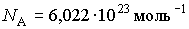 . В соответствии с формулой (5.113), величина относительных флуктуаций температуры для рассматриваемого газового термометра приближенно равна . В соответствии с формулой (5.113), величина относительных флуктуаций температуры для рассматриваемого газового термометра приближенно равна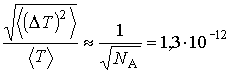 . .Очевидно, что столь малое значение флуктуаций температуры зарегистрировать практически невозможно.
|
|
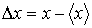 .
.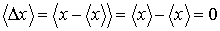 .
.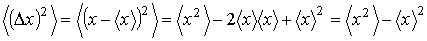 .
.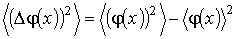 .
.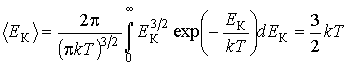 ,
,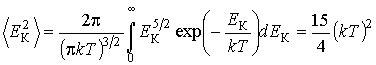 .
.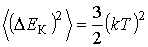 .
.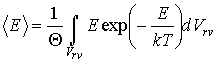 ,
,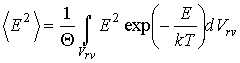 .
.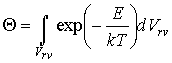 .
.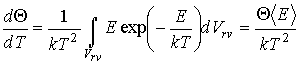 .
.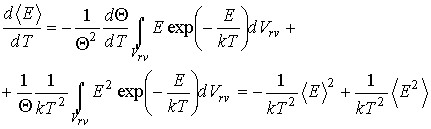
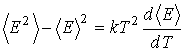 .
.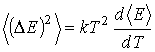 .
.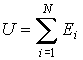 .
.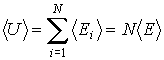 ,
,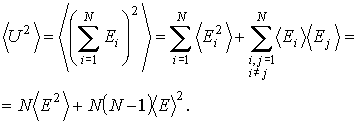
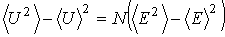
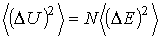 .
.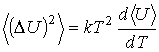 ,
,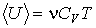 ,
,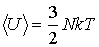 .
.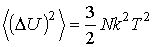 .
.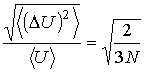 .
.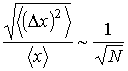 .
.