|
|
|||
|
|||
|
ГЛАВА 5
5.6. Распределение Максвелла-Больцмана |
|
Полученные в предыдущих параграфах распределения Больцмана (5.23) и Максвелла (5.62) описывают зависимость концентрации молекул от координат
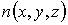 и функцию распределения по скоростям и функцию распределения по скоростям  соответственно. При этом распределение Больцмана описывается в пространстве координат соответственно. При этом распределение Больцмана описывается в пространстве координат 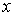 , , 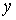 и и 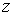 , а распределение Максвелла в пространстве скоростей , а распределение Максвелла в пространстве скоростей 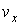 , , 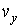 и и 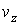 . .Если ввести 6-мерное пространство, координатами молекулы в котором являются величины
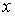 , , 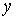 , , 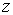 , , 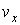 , , 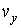 и и 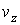 , то функция распределения в таком пространстве будет зависеть от этих шести переменных: , то функция распределения в таком пространстве будет зависеть от этих шести переменных: 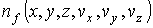 . Считая пространственные переменные . Считая пространственные переменные 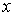 , , 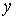 , , 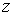 и компоненты скорости и компоненты скорости 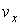 , , 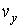 , , 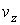 статистически независимыми друг от друга, на основании формулы (5.10) можно записать: статистически независимыми друг от друга, на основании формулы (5.10) можно записать:
или
где выражение для кинетической энергии имеет вид:
Формула (5.77) называется функцией распределения Максвелла-Больцмана. Она может быть использована в случае, когда полная энергия молекулы
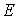 равна сумме её потенциальной энергий равна сумме её потенциальной энергий 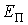 во внешнем силовом поле и кинетической энергии во внешнем силовом поле и кинетической энергии 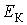 её поступательного движения: её поступательного движения: 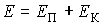 . .При получении закона распределения Максвелла-Больцмана предполагалось, что температура газа не зависит от координаты точки. В частности, температура газа на всех высотах над поверхностью Земли при термодинамическом равновесии должна быть одинакова. С этим утверждением связан парадокс, всесторонне рассмотренный Максвеллом. Дело в том, что при движении вверх молекулы газа должны затрачивать свою кинетическую энергию на преодоление силы тяжести, и поэтому их средняя кинетическая энергия (а следовательно и температура) должна уменьшаться. Но этого не происходит вследствие того, что при этом не все молекулы, из-за недостатка их кинетической энергии, смогут преодолеть силу тяжести. Молекулы, имеющие недостаточную кинетическую энергию, не могут подняться высоко, что приведет, в соответствии с распределением Больцмана, к уменьшению их концентрации с высотой. Поэтому температура газа останется неизменной.
Функция распределения в более общем случае, когда кинетическая энергия зависит только от скорости
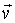 , а потенциальная - только от радиус-вектора , а потенциальная - только от радиус-вектора 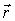 микрочастицы, имеет вид: микрочастицы, имеет вид:
где постоянная
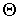 определяется из условия нормировки (5.5): определяется из условия нормировки (5.5):
Здесь:
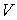 - объем, занимаемый системой в координатном пространстве, - объем, занимаемый системой в координатном пространстве, 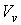 - соответствующий объем в пространстве скоростей. - соответствующий объем в пространстве скоростей.Формула (5.79) позволяет описывать равновесное распределение для достаточно произвольной термодинамической системы.
Полученные выше функции распределения описывают случай, когда полная энергия частицы
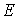 принимает непрерывный ряд значений. При статистическом описании системы, частицы которой могут принимать только некоторый дискретный набор значений энергии принимает непрерывный ряд значений. При статистическом описании системы, частицы которой могут принимать только некоторый дискретный набор значений энергии 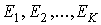 , необходимо использовать вместо функции распределения вероятность нахождения частицы в состоянии со значением энергии , необходимо использовать вместо функции распределения вероятность нахождения частицы в состоянии со значением энергии 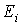 : : 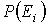 . В случае дискретных состояний можно записать следующее выражение для этой вероятности . В случае дискретных состояний можно записать следующее выражение для этой вероятности 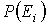 : :
где величина
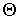 определяется из условия нормировки (5.2): определяется из условия нормировки (5.2):
Если полное число частиц в системе равно
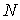 , то число частиц , то число частиц 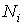 в состоянии с энергией в состоянии с энергией 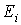 определяется по формуле: определяется по формуле:
Формула (5.81) называется распределением Больцмана для дискретных состояний.
Задача 5.4. Рассчитать среднее значение полной энергии случайных тепловых колебаний тела, подвешенного на пружине (осциллятора).
Решение: Кинетическая энергия тела, совершающего одномерные колебания имеет вид:
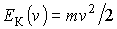 , ,а потенциальная энергия соответственно равна:
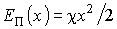 , ,где:
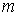 - масса тела, - масса тела, 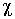 - жесткость пружины. - жесткость пружины.Функцию распределения для рассматриваемого случая в соответствии с формулами (5.79) и (5.80) можно записать в виде
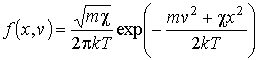 . .Среднее значение полной энергии равно сумме средних значений кинетической и потенциальной энергий:
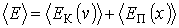 , ,которые, в соответствии с формулой (5.6), равны:
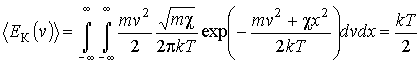 , ,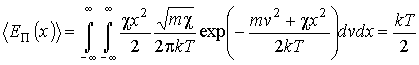 . .Таким образом, средние значения кинетической и потенциальной энергии равны между собой. А среднее значение полной энергии осциллятора равно удвоенному значению кинетической (или потенциальной) энергии:
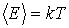 . . |
|
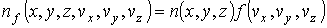
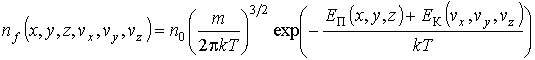 ,
,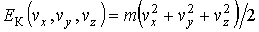 .
.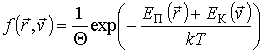 ,
,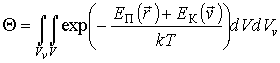 .
.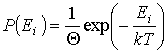 ,
,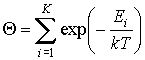 .
.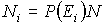 .
.