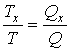|
|
|||
|
|||
|
ГЛАВА 3
3.6. Термодинамическая шкала температур |
|
Теорема Карно позволяет построить рациональную температурную шкалу, преимуществом которой является ее независимость от термодинамических свойств используемого термометрического тела. По этой причине термодинамический термометр имеет более фундаментальное значение, чем использованные в первой главе при введении понятия температуры.
Прежде чем приступить к построению термодинамической шкалы температур проведем более подробное доказательство соотношения, следующего из сопоставления формул (3.2), (3.30) и (3.32):
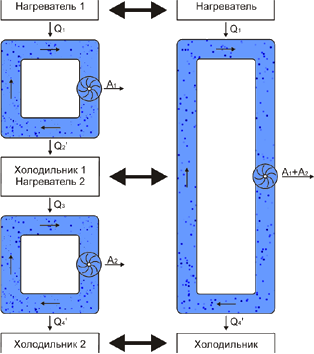
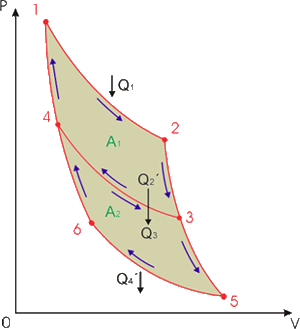
Для этого рассмотрим две работающие по циклу Карно тепловые машины, причем холодильник первой выступает в качестве нагревателя второй машины. Сравним к.п.д. такой системы, состоящей из двух тепловых машин и к.п.д. объединенной тепловой машины, нагревателем которой выступает нагреватель первой, а холодильником - холодильник второй машины (см. рис. 3.7). При этом теплота 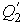 отнимаемая холодильником первой машины равна теплоте отнимаемая холодильником первой машины равна теплоте 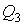 передаваемой второй: передаваемой второй: 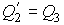 , а суммарная работа двух тепловых машин равна работе объединенной тепловой машины. , а суммарная работа двух тепловых машин равна работе объединенной тепловой машины.
На рис. 3.8. представлены термодинамические циклы рассматриваемых тепловых машин. Круговой процесс 1-2-3-4-1 соответствует первой тепловой машине, процесс 4-3-5-6-4 - второй машине, а процесс 1-2-5-6-1 описывает составную тепловую машину.

Пусть изотермический процесс 1-2 происходит при температуре
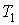 , процесс 3-4 (или процесс 4-3) при температуре , процесс 3-4 (или процесс 4-3) при температуре 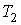 , а процесс 5-6 при температуре , а процесс 5-6 при температуре 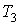 . Применение первой теоремы Карно для трех рассматриваемых процессов позволяет записать следующие выражения: . Применение первой теоремы Карно для трех рассматриваемых процессов позволяет записать следующие выражения:
Деление формулы (3.36) на (3.34) и сравнение получившегося выражения с формулой (3.35), с учетом равенства
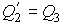 , дает тождество , дает тождество
которое должно выполняться для любых значений температур
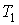 , , 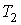 и и 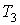 . Учитывая, что левая часть этого выражения не зависит от температуры . Учитывая, что левая часть этого выражения не зависит от температуры  , правая часть тоже не должна зависеть от этой температуры. А это возможно только, если функция , правая часть тоже не должна зависеть от этой температуры. А это возможно только, если функция 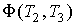 представима в виде представима в виде
Следовательно, можно утверждать, что для цикла Карно выполняется следующее условие:
Величина
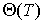 представляет собой термодинамическую температуру и при сопоставлении ее с идеально-газовой шкалой может быть представлена в виде: представляет собой термодинамическую температуру и при сопоставлении ее с идеально-газовой шкалой может быть представлена в виде: 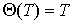 , где температура , где температура 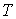 задается шкалой Кельвина. Следовательно, шкала температур, построенная с использованием идеально-газового термометра, и термодинамическая шкала температур совпадают. задается шкалой Кельвина. Следовательно, шкала температур, построенная с использованием идеально-газового термометра, и термодинамическая шкала температур совпадают.Таким образом, цикл Карно позволяет построить термодинамическую шкалу температур и предложить термодинамический термометр. Принцип действия такого термометра заключается в организации цикла Карно между телом с неизвестной температурой
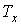 и телом с известной температурой и телом с известной температурой 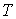 (например, с тающим льдом или кипящей водой) и измерении соответствующего количества теплоты (например, с тающим льдом или кипящей водой) и измерении соответствующего количества теплоты 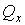 и и 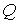 . Применение формулы . Применение формулы
позволяет вычислить температуру тела. Очевидно, что практическая реализация такого термометра достаточно затруднительна, так как при этом необходимо организовать протекание в какой-либо тепловой машине термодинамического цикла Карно, а также измерить количества теплоты
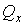 и и 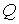 . .Однако, даже при независимости рассмотренного термометра от использованного в нем термометрического тела (рабочего тела цикла Карно), необходима привязка его показаний к реперным точкам, определяемым термодинамическими свойствами эталонов температуры, например к точке замерзания воды.
|
|
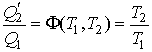 .
.
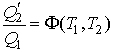 ,
,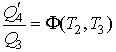 ,
,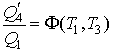 .
.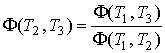 ,
,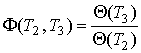 .
.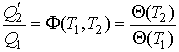 .
.