|
|
|||
|
|||
|
ГЛАВА 3
3.5. Теорема Карно |
|
Приведенные выше рассуждения позволяют перейти к формулировке первой и второй теорем Карно. Их можно сформулировать в виде двух следующих утверждений:
1. Коэффициент полезного действия любой обратимой тепловой машины, работающей по циклу Карно, не зависит от природы рабочего тела и устройства машины, а является функцией только температуры нагревателя
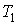 и холодильника и холодильника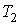 : :
2. Коэффициент полезного действия любой тепловой машины, работающей по необратимому циклу, меньше коэффициента полезного действия машины с обратимым циклом Карно, при условии равенства температур их нагревателей и холодильников:
Отметим также, что к.п.д. любой обратимой тепловой машины равен к.п.д. цикла Карно при равенстве температур их нагревателей и холодильников.
Проведем доказательство первой теоремы Карно. Пусть имеются две тепловые машины с общим нагревателем и холодильником, работающие по циклу Карно, но имеющие различные к.п.д., вследствие, например, различного устройства или отличия физический природы рабочего тела. Предположим, что к.п.д. первой тепловой машины больше чем у второй:
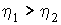 . Тогда, запустив первую машину по прямому циклу Карно, а вторую по обратному (это всегда можно сделать вследствие обратимости цикла Карно) и соединив их вместе так, чтобы одна машина могла совершать работу над другой, можно будет в такой системе или получать механическую работу за счет отбора теплоты от холодильника, или передавать часть теплоты от холодильника к нагревателю. Реализация той или иной возможности зависит от конкретной технической реализации рассматриваемой системы из двух тепловых машин. Как первый, так и второй результат работы такой системы противоречит второму началу термодинамики. Аналогичные рассуждения можно выполнить и в случае, когда . Тогда, запустив первую машину по прямому циклу Карно, а вторую по обратному (это всегда можно сделать вследствие обратимости цикла Карно) и соединив их вместе так, чтобы одна машина могла совершать работу над другой, можно будет в такой системе или получать механическую работу за счет отбора теплоты от холодильника, или передавать часть теплоты от холодильника к нагревателю. Реализация той или иной возможности зависит от конкретной технической реализации рассматриваемой системы из двух тепловых машин. Как первый, так и второй результат работы такой системы противоречит второму началу термодинамики. Аналогичные рассуждения можно выполнить и в случае, когда 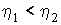 . Таким образом, для всех тепловых машин, работающих по обратимому циклу Карно, их к.п.д. должен быть одинаков при одинаковых температурах нагревателей и холодильников. . Таким образом, для всех тепловых машин, работающих по обратимому циклу Карно, их к.п.д. должен быть одинаков при одинаковых температурах нагревателей и холодильников.Вторая теорема Карно может быть обоснована тем, что при протекании необратимого кругового процесса неизбежно произойдет преобразование части работы в теплоту, вследствие происходящих внутри машины диссипативных процессов, связанных с релаксацией неоднородностей внутри рабочего тела или трением движущихся частей. Это приведет к уменьшению механической работы и, в соответствии с формулой (3.2), к уменьшению к.п.д. тепловой машины в сравнении с идеальной машиной Карно. Следовательно, к.п.д. необратимой тепловой машины всегда будет меньше к.п.д. цикла Карно, если температуры их нагревателей и холодильников одинаковы.
Сравнение формул для к.п.д. цикла Карно тепловой машины, работающей на идеальном газе (3.13), и приведенной выше формулы (3.30) позволяет записать математическую формулировку первой теоремы Карно в следующем виде:
Возможность применения формулы (3.32) для расчета к.п.д. любой обратимой тепловой машины связана с тем, что вид функции
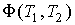 для всех рабочих тел, в том числе и для идеального газа, должен быть одинаков. для всех рабочих тел, в том числе и для идеального газа, должен быть одинаков. |
|
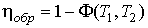 ;
;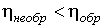 .
.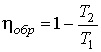 .
.