
. . . . .
..:: 1.5. Первое начало термодинамики ::..
|
|
|
В предыдущем параграфе была рассмотрена термодинамическая система, помещённая в адиабатическую оболочку. Однако, большинство термодинамических систем такой оболочки не имеют и находятся в состоянии постоянного теплообмена с окружающими телами. Первое начало термодинамики утверждает, что изменение внутренней энергии термодинамической системы (тела) может быть осуществлено двумя путями: путём совершения механической работы и путём теплопередачи. Энергия, переданная системе путём теплопередачи, называется количеством теплоты Q. Таким образом, количество теплоты может быть определено как разность изменения внутренней энергии системе и механической работы, совершённой над системой. Математически это может быть записано как где Q - количество теплоты, переданной системе, dU - изменения внутренней энергии системы, A` - работа, совершённая над системой. Так как работа, совершенная над системой A`, равна работе, совершенной системой A, взятой с обратным знаком: A` = - A , то первое начало термодинамики может быть сформулировано следующим образом: Теплота Q, подводимая к системе, идет на изменение ее внутренней энергии dU и на совершение этой системой работы A над внешними телами: Если к термодинамической системе подводится элементарное количество теплоты Отметим принципиальное отличие величины 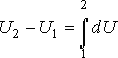 (1.6) (1.6) Интегралы (суммы) от величин 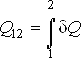 (1.7) (1.7)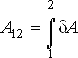 (1.8) (1.8)Таким образом, необходимо отметить принципиальную разницу между внутренней энергией, являющейся функцией состояния, и теплотой и работой, которые не являются функциями состояния, а зависят от того, каким образом система переведена из одного состояния в другое. С учетом формул (1.6)-(1.8) интегрирование выражения (1.5) дает
Q12 = U2 - U1 + A12 (1.9)
Эта формула представляет собой запись первого начала термодинамики применительно к случаю перехода термодинамической системы из некоторого первого состояния во второе. По своему физическому смыслу первое начало термодинамики представляет собой закон сохранения (изменения) энергии в термодинамике. Если согласно закону сохранения энергии в механике, работа неконсервативных сил равна приращению механической энергии системы (в частности, работа диссипативных сил равна уменьшению механической энергии системы), то согласно первому началу термодинамики, приращение внутренней энергии термодинамической системы равно сумме работы всех сил и энергии, переданной системе путём теплопередачи. Причём, эти силы (как и в механике) могут быть как внешними, так и внутренними. Например, в опыте Джоуля, работа внешних сил приводит к увеличению внутренней механической энергии воды в неравновесном состоянии (возникновению в ней потоков), а работа внутренних сил трения переводит эту механическую энергию во внутреннюю тепловую энергию воды в равновесном состоянии (кинетическую энергию микроскопического движения молекул воды). В опыте Джоуля пренебрегалось изменением объёма воды (хотя именно изменения объёма воды характеризуют при неизменном внешнем давлении изменение состояния воды) и считалось, что механическая работа совершается без изменения объёма системы. При этом работа диссипативных сил (вязкого трения) приводила к росту внутренней энергии системы. Аналогичная ситуация имеет место, когда тело скользит по шероховатой поверхности. Силы трения, действующие на тело со стороны поверхности, приводят к увеличению внутренней энергии тела, и силы трения, действующие на поверхность, приводят к увеличению внутренней энергии поверхности, причём суммарное увеличение внутренней энергии тела и поверхности равно механической работе сил трения. Если бы в опыте Джоуля силы вязкого трения отсутствовали (например, вместо воды был не имеющий вязкости сверхтекучий гелий), то вся потенциальная энергия опускающихся грузов переходила бы в их кинетическую энергию и кинетическую энергию шкивов без изменения термодинамического состояния жидкости. Другая ситуация имеет место в случае, если учитывать изменение объёма тела, но пренебрегать внутренними силами трения в нём. Примером такой системы является идеальный газ. Тогда механическая работа, совершаемая телом, будет определяться механическим движением границы тела (все внутренние движения из-за отсутствия трения не приведут к совершению работы). Без учета изменения потенциальной энергии тела вследствие наличия гравитационных или электромагнитных полей, работа, совершенная телом, определяется двумя параметрами - давлением и объёмом. В случае, если термодинамические процессы в системе - квазиравновесные, то термодинамическое потоки в ней отсутствуют, и можно пренебречь вязким трением, считая, что изменения объёма и давления определяют изменение состояния системы. Связь между объёмом и давлением может быть задана с помощью температуры. Работа где P - внешнее давление, действующее на тело. Если это давление одно и то же во всех точках поверхности тела, то просуммировав по всей поверхности получим: где 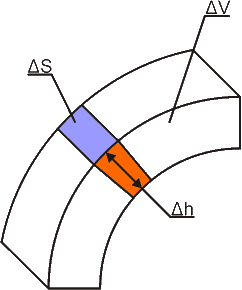 Рис. 1.4. Элементарная работа при изменении объема термодинамической системы. Для элементарной работы Работа при конечных изменениях объёма тела может быть определена путем интегрирования выражения (1.12): 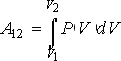 (1.13) (1.13)Этот интеграл зависит от пути перехода из состояния 1 в состояние 2, так как вид функции P(V) зависит от пути перехода. Указанная зависимость величины интеграла (1.13) может быть проиллюстрирована рис. 1.5, из которого видно, что работа A12 равна площади под кривой P(V). 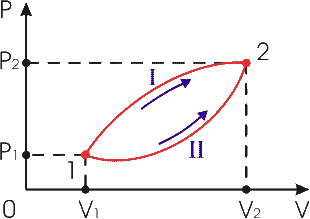 Рис. 1.5. Работа при переходе из одного состояния термодинамической системы в другое В зависимости от траектории I или II перехода из первого состояния во второе площадь под кривой P(V) будет различна, а, следовательно, будет различна работа этих термодинамических процессов. Количество теплоты Q12, необходимое для перехода из первого состояния во второе, также будет зависеть от формы траектории. В этом можно убедится, если учесть, тот факт, что внутренняя энергия является функцией состояния термодинамической системы, и ее изменение при переходе из первого состояния во второе не зависит от пути этого перехода. А, следовательно, в соответствии с первым началом термодинамики (см. формулу (1.4)) теплота, также как и работа, должна зависеть формы траектории термодинамического процесса. Задача 1.2. Определить изменение внутренней энергии газа в адиабатической оболочке, совершающего расширение при постоянном давлении P. Начальный объем газа равен V1, конечный - V2. Решение: Согласно первому началу термодинамики (см. формулу (1.9)) при Q12=0 (условие адиабатической оболочки) имеем: U2 - U1 = -A12 = -P(V2 - V1) = P(V1 - V2).
При вычислении работы была использовано формула (1.13). Задача 1.3. Найти работу, совершаемую газом, при его расширении от объема V1 до V2 объема, если зависимость давления от объема V выражается формулой: Решение: В соответствии с формулой (1.13) имеем: 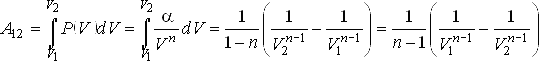 |
2000-2001© кафедра ФИЗИКИ МГТУ