Часть I. Основные способы вычисления пределов, содержащих неопределенности типа .

1. Подставить в выражение предельное значение аргумента.
2. Определить есть или нет неопределенность. Если нет, дать ответ.
3. Если неопределенность есть, то по ее виду выбрать одно из правил устранения этой неопределенности.
4. Преобразовать выражение согласно выбранному правилу, и к новой форме предела применить данный алгоритм, начиная с п.1.

В числителе и знаменателе вынести x в максимальной степени, если это возможно. Заметим, что , а , где c - любое число.

Числитель и знаменатель разделить одновременно на , если это возможно. Необходимо иметь в виду, что , а , где c - число, отличное от нуля.

При вычислении пределов от иррациональных выражений, не попадающих в предыдущие правила, следует избавиться от корней, входящих в неопределенность. Возможны следующие способы:

3.1. замена переменной , позволяющая извлечь корни, входящие в неопределенность;

3.2. дополнение до формулы, позволяющей возвести корень в соответствующую ему степень; здесь используются формулы:  ; .

Например, , т.е. умножили и разделили на сопряженное выражение.

При наличии неопределенности в пределе от выражения, содержащего тригонометрические функции, следует выделить в этом выражении первый замечательный предел:

 .    (1)

Можно использовать следствия этого предела:

 ;     (2)

 ;     (3)

 ;     (4)

 .     (5)

Вычисление предела сложнопоказательной функции. .

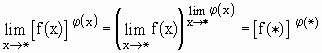Если рассматриваемый предел содержит неопределенность , то он сводится ко второму замечательному пределу:

     (1)

или   .     (2)

Предел сложной функции:.

В частности, , если.

Необходимо помнить свойства логарифмов : , , , . Есть пределы, которыми можно пользоваться как "табличными":

,     (1)

,     (2)

,     (3)

.     (4)

Назад |  В начало |  Дальше