- Details
- Category: Научная работа
Публикации сотрудников кафедры ФН-12 Математическое моделирование
|
Статьи в журналах/сборниках из перечня Web of Science/Scopus |
||
| 1 | Akimova A.A., Manturov V.O. Labels instead of coefficients: A label bracket [•] L which dominates the Jones polynomial [•], the Kuperberg bracket [•] A 2, and the normalized arrow polynomial [•] // Journal of Knot Theory and Its Ramifications 2020 .- Vol. 29 , Issue 2 .- Art.no 2040001. | 2020 |
| 2 | Chetverikov V.N. Invertible linear ordinary differential operators and their generalizations // Journal of Geometry and Physics 2020 .- Vol. 151 .- Art.no 103617. | 2020 |
| 3 | Kanatnikov A.N., Krishchenko A.P. Qualitative Properties of a Duffing System with Polynomial Nonlinearity // Proceedings of the Steklov Institute of Mathematics 2020 .- Vol. 308 , Issue 1 .- pp. 184 - 195. | 2020 |
| 4 | Kirillov A.A., Savelova E.P. Wormhole as a possible accelerator of high-energy cosmic-ray particles // The European Physical Journal C 2020 .- Vol. 80 , Issue 1 .- Art.no 45. | 2020 |
| 5 | Krasnova S.A. Estimating the Derivatives of External Perturbations Based on Virtual Dynamic Models // Automation and Remote Control 2020 .- Vol. 81 , Issue 1 .- pp. 897 - 910. | 2020 |
| 6 | Krishchenko A.P., Starkov K.E. Convergence dynamics in one eco-epidemiological model: Self-healing and some related results // Communications in Nonlinear Science and Numerical Simulation 2020 .- Vol. 85 .- Art.no 10522. | 2020 |
| 7 | Manturov V.O., Ilyutko D.P. Picture-valued parity-biquandle bracket // Journal of Knot Theory and Its Ramifications 2020 .- Vol. 29 , Issue 2. | 2020 |
| 1 | Attetkov A.V., Vlasov P.A., Volkov I.K. Stationary Temperature Field of a Separation System with Active Thermal Protection Possessing Feedback and Anisotropic Coating // High Temperature 2019 .- Vol. 57 , Issue 6 .- pp. 878 - 884. | 2019 |
| 2 | Bednov B.B. The Set of Geometric Medians for Four-Element Subsets in Lindenstrauss Spaces// Moscow University Mathematics Bulletin 2019 .- Vol. 74 , Issue 6 .- pp. 215 - 220. | 2019 |
| 3 | Belinskaya J.S., Makarov D. Comparison of flatness-based and model predictive control approaches // 12th International Conference ""Management of Large-Scale System Development"", MLSD 2019 2019 .- Art.no 8911043 | 2019 |
| 4 | Belov I.R., Yurchenkov A.V., Kustov A.Yu. Anisotropy-based bounded real lemma for multiplicative noise systems: The finite horizon case // 7th Mediterranean Conference on Control and Automation, MED 2019 - Proceedings 2019 .- pp. 148 - 152. | 2019 |
| 5 | Biryukov O.N. Parity conditions for realizability of Gauss diagrams // Journal of Knot Theory and Its Ramifications 2019 .- Vol. 28 , Issue 1. | 2019 |
| 6 | Botkin N.D., Golubev A.E., Turova V.L. Aircraft Guiding in Windshear through Differential Game-Based Overload Control // IFAC-PapersOnLine 2019 .- Vol. 52 , Issue 16 .- pp. 706 - 711. | 2019 |
| 7 | Chetverikov V.N. Input-Output Systems and Backlund Transformations // Differential Equations 2019 .- Vol. 55 , Issue 10 .- pp. 1397 - 1406. | 2019 |
| 8 | Fetisov D.A. On Some Approaches to Linearization of Affine Systems // IFAC-PapersOnLine 2019 .- Vol. 52 , Issue 16 .- pp. 700 - 705. | 2019 |
| 9 | Fursov A.S., Kapalin I.V. Some Approaches to Stabilizing Switched Linear Systems with Operation Modes of Different Dynamic Orders // Differential Equations 2019 .- Vol. 55 , Issue 12 .- pp. 1641 - 1648. | 2019 |
| 10 | Fursov A.S., Minyaev S.I., Mosolova Yu. M. Synthesis of a digital output controller for a switched interval linear system // Differential Equations 2019 .- Vol. 55 , Issue 11 .- pp. 1503 - 1517. | 2019 |
| 11 | Glazkov T.V., Reshmin S.A. A nonlinear tire model to describe an unwanted flat vibrations of the wheels // IFAC-PapersOnLine 2019 .- Vol. 52 , Issue 16 .- pp. 268 - 273. | 2019 |
| 12 | Glazkov T.V., Golubev A.E., Gorbunov A.V., Krishchenko A.P. Control of Quadcopter Motion in the Horizontal Plane // AIP Conference Proceedings 2019 .- Т. 2116 .- Art.no 380003. | 2019 |
| 13 | Glazkov T.V., Golubev A.E. Using Simulink support package for Parrot Minidrones in nonlinear control education // AIP Conference Proceedings 2019 .- Vol. 2195. | 2019 |
| 14 | Golubev A.E., Botkin N.D., Krishchenko A.P. Backstepping control of aircraft take-off in windshear // IFAC-PapersOnLine 2019 .- Vol. 52 , Issue 16 .- pp. 712 - 717. | 2019 |
| 15 | Golubev A.E., Thway N., Gorbunov A.V., Krishchenko A.P., Utkina N.V. Construction of quadrocopter programmed motion in a flat labyrinth // AIP Conference Proceedings 2019 .- Т. 2116 .- Art.no 380004. | 2019 |
| 16 | Golubev A.E., Krishchenko A.P., Utkina N.V. Construction of quadrocopter programmed motion in a flat labyrinth // AIP Conference Proceedings 2019 .- Т. 2116 .- Art.no 380004. | 2019 |
| 17 | Goryainov V.B., Goryainova E.R. Comparative Analysis of Robust and Classical Methods for Estimating the Parameters of a Threshold Autoregression Equation // Automation and Remote Control 2019 .- Vol. 80 , Issue 4 .- pp. 666 - 675. | 2019 |
| 18 | Gribov A.F., Shaktarin B.I. Effect of Higher Harmonics on the Accurate Calculation of Dynamic Phase-Locked-Loop Characteristics Using the Quasi-Harmonic Method // Journal of Communications Technology and Electronics 2019 .- Vol. 64 , Issue 5 .- pp. 484 - 491. | 2019 |
| 19 | Il'in A.V., Fomichev V.V., Fursov A.S. Control Problems for Systems with Uncertainty // Computational Mathematics and Modeling 2019 .- Vol. 30 , Issue 4 .- pp. 390 - 402. | 2019 |
| 20 | Ivankov P.L. On Differentiation with Respect to Parameter of a Hypergeometric Function of a Special Type // Russian Mathematics 2019 .- Vol. 63 , Issue 12 .- pp. 61 - 70. | 2019 |
| 21 | Ivankov P.L. On Linear Independence of Differentiated with Respect to Parameter Functions and Their Values // Russian Mathematics 2019 .- Vol. 63 , Issue 9 .- pp. 22 - 30. | 2019 |
| 22 | Ivanov A.O., Tuzhilin A.A. Isometry group of Gromov-Hausdorff space // Matematicki Vesnik 2019 .- Vol. 71 , No 1-2 .- pp. 123 - 154. | 2019 |
| 23 | Ivanov A.O., Nikolaeva N.K., Tuzhilin A.A. Steiner Problem in the Gromov-Hausdorff Space: The Case of Finite Metric Spaces // Proceedings of the Steklov Institute of Mathematics 2019 .- Vol. 304 .- pp. S88 - S96. | 2019 |
| 24 | Ivanov A.O., Tuzhilin A.A. Steiner type ratios of Gromov-Hausdorff space // European Journal of Combinatorics 2019 .- Vol. 80 .- pp. 172 - 183. | 2019 |
| 25 | Kanatnikov A.N. Localizing sets and behavior of trajectories of time-varying systems // Differential Equations 2019 .- Vol. 55 , Issue 11 .- pp. 1420 - 1430. | 2019 |
| 26 | Kim S., Manturov V.O. Artin's braids, braids for three space, and groups σn4 and Gnk // Journal of Knot Theory and Its Ramifications 2019 .- Vol. 28 , Issue .10 .- Art.no 1950063. | 2019 |
| 27 | Kirillov A.A., Savelova E.P. On distortion of the background radiation spectrum by wormholes: kinematic Sunyaev-Zel'dovich effect // Astrophysics and space science 2019 .- Т. 364 , № 1 .- pp. 1. | 2019 |
| 28 | Krasnova S.A., Antipov A.S. Block synthesis of tracking system for inverted pendulum via sigmoidal feedbacks // Proceedings - 2019 International Russian Automation Conference, RusAutoCon 2019.- Art.no 8867695. | 2019 |
| 29 | Krishchenko A.P. Behavior of Trajectories of the Levinson - Smith Equation // Differential Equations 2019 .- Vol. 55 , Issue 11 .- pp. 1431 - 1439. | 2019 |
| 30 | Krishchenko A.P., Kuvyrkin G.N. Preface of the Symposium “Mathematical Modeling in Applied Research” // AIP Conference Proceedings 2019 .- Т. 2116 : International Conference on Numerical Analysis and Applied Mathematics (ICNAAM-2018) .- Art.no 380001. | 2019 |
| 31 | Krishchenko A.P. Trajectories Behavior of the Duffing Equation with External Unknown Forcing // AIP Conference Proceedings 2019 .- Т. 2116 .- Art.no 380002. | 2019 |
| 32 | Pankratov V.A., Litun S.I. Aerodynamic Parameters Identification of the Nanosatellite TNS-0 No 2 to Enhance Ballistic Calculations Precision for Low-Flying Satellites // Proceedings of 2019 12th International Conference (Management of Large-Scale System Development), MLSD 2019 2019 .- Art.no 8911071. | 2019 |
| 33 | Reshmin S.A., Glazkov T.V. Nonlinear Reduced-Order Model for Simulating Flat Vibrations of the Vehicle Driving Wheels // Proceedings - 21st International Conference "Complex Systems: Control and Modeling Problems".- Vol. 2019-September .- pp. 586 - 591. | 2019 |
| 34 | Reshmin S.A. Qualitative Analysis of the Undesirable Effect of Loss of Traction Force of a Vehicle during an Intense Start // Doklady Physics 2019 .- Vol. 64 , Issue 1 .- pp. 30 - 33. | 2019 |
| 35 | Reshmin S.A. The analysis of the loss of the traction effect during an intensive start of a vehicle // Journal of Computer and Systems Sciences International 2019 .- Vol. 58 , Issue 3 .- pp. 349 - 359. | 2019 |
| 36 | Shelyganova O.I., Krasnova S.A. Modeling of the process of registration of estimate-contractual documentation // Contemporary problems of social work 2019 .- Vol. 5 , Issue 1(17) .- pp. 26 - 34. | 2019 |
| 37 | Smirnov A.E., Fakhurtdinov R.S., Ryzhova M.Y., Pakhomova S.A. Technological Features of Vacuum Carburizing of Low-Alloyed Steels // Journal of Machinery Manufacture and Reliability 2019 .- Vol. 48 , Issue 2 .- pp. 167 - 172. | 2019 |
| 38 | Timin V.N., Kustov A.Yu., Kurdyukov A.P., Goldin D.A., Vershinin Y.A. Suboptimal Anisotropic Filtering for Linear Discrete Nonstationary Systems with Uncentered External Disturbance // Automation and Remote Control 2019 .- Vol. 80 , Issue 1 .- pp. 1 - 15. | 2019 |
| 39 | Utkin V.A., Utkin A.V., Krasnova S.A. Control Systems with Limitations on Controls and their Derivatives // Proceedings - 2019 International Russian Automation Conference, RusAutoCon 2019 .- Art.no 8867745. | 2019 |
| 40 | Utkin V.A., Krasnova S.A. Improving the Accuracy of the Estimated Signals in the State and Disturbance Observer // Proceedings of 12th International Conference "Management of large-scale system development", MLSD 2019 .- Art.no 8911009. | 2019 |
| 41 | Vasil`eva M.V., Ivleva M.I., Volkov Yu.G., Karaev A.K., Nikitina N.I., Poszorova M.I. The development of meta-competencies in undergraduate students using personality development theory // OPCION 2019.- Vol. 35, Issue Special 23 .- pp. 1524 - 1543. | 2019 |
| 42 | Vlasov P.A. Condition for the Existence of the Optimal Wall Thickness Dividing Two Different Environments with Local Heat Exposure // High Temperature 2019 .- Vol. 57 , Issue 5 .- pp. 694 - 699. | 2019 |
| 43 | Volkov B.O. Levy differential operators and Gauge invariant equations for Dirac and Higgs fields // Infinite Dimensional Analysis, Quantum Probability and Related Topics 2019 .- Vol. 22 , Issue 1. | 2019 |
| 44 | Volkov B.O. Levy Laplacian on Manifold and Yang - Mills Heat Flow // Lobachevskii Journal of Mathematics 2019 .- Vol. 40 , Issue 10 .- pp. 1619 - 1630. | 2019 |
|
1 |
Antipov A.S., Krasnova S.A. Decomposition synthesis of invariant systems with nonlinear local feedbacks // Proceedings of 2018 14th International Conference Stability and Oscillations of Nonlinear Control Systems (Pyatnitskiys Conference), STAB 2018, 2018 .- С. 1 - 4. |
2018 |
| 2 | Antipov A.S., Krasnova S.A. The block synthesis of the tracking system with sigmoidal local feedbacks // Proceedings of 2018 11th International Conference "Management of Large-Scale System Development", MLSD 2018 2018 .- Art.no 8551923. |
2018 |
|
3 |
Attetkov A.V., Vlasov P.A., Volkov I.K. The Conditions for the Existence of the Optimal Thickness of a Cooled Anisotropic Wall Subjected to Local Heat Exposure // High Temperature 2018 .- Vol. 56 , Issue 3 .- С. 389 - 392. |
2018 |
| 4 | Barkin M.Yu., Pankratov V.A. Considering the Motion of the Elastic Lunar Pole // IOP Conference Series: Materials Science and Engineering 2018 2018 .- Vol. 458 , Issue 1 .- Art.no 012042. |
2018 |
| 5 | Bednov B.B., Borodin P.A., Chesnokova K.V. Existence of Lipschitz selections of the Steiner map // Sbornik Mathematics 2018 .- Vol. 209 , Issue 2 .- С. 145 - 162. |
2018 |
|
6 |
Belinskaya Y.S., Chetverikov V.N. Covering Method for Trajectory Generation and Orbital Decomposition of Systems // Differential Equations 2018 .- Vol. 54 , Issue 4 .- С. 497 - 508. |
2018 |
| 7 | Blokhina O.A., Beketova O.N., Kuzmina E.E., Lebedeva O.Y., Podzorova M.I. Improving the technology of innovation systems management at an enterprise // International Journal of Civil Engineering and Technology 2018 .- Vol. 9 , Issue 13 .- С. 137 - 143. |
2018 |
| 8 | Fetisov D.A. A-Orbital Linearization of Affine Systems // Differential Equations 2018 .- Vol. 54 , No 11 .- С. 1494 - 1508. |
2018 |
| 9 | Fetisov D.A. To the Linearization Problem for Single-Input Control Affine Systems // Journal of Physics: Conference Series 2018 .- Vol. 1141 , No 1 .- Art.no 012120. |
2018 |
|
10 |
Fursov A.S., Minyaev S.I., Guseva V.S. Digital Stabilizer Design for a Switched Linear Control Delay System // Differential Equations 2018 .- Vol. 54 , No 8 .- С. 1115 - 1124. |
2018 |
| 11 | Fursov A.S., Emel'yanov S.V., Kapalin I.V., Sagadinova E.S. Stabilization of Multiple-Input Switched Linear Systems with Operation Modes of Different Dynamical Orders // Differential Equations 2018 .- Vol. 54 , Issue 11 .- С. 1517 - 1523. |
2018 |
|
12 |
Goryainov A.V., Goryainov A.V. M-Estimates of Autoregression with Random Coefficients // Automation and Remote Control 2018 .- Vol. 79 , Issue 8 .- С. 1409 - 1421. |
2018 |
|
13 |
Gribov A.F. Localization of Invariant Compacts in Multidimensional Systems with Phase Control // Automation and Remote Control 2018 .- Vol. 79 , Issue 8 .- С. 1330 - 1398. |
2018 |
| 14 | Il’in A.V., Fursov A.S., Mal’tseva A.V. Generalization of the internal approximation method for the simultaneous stabilization problem // Differential Equations 2018 .- Vol. 54 , Issue 12 .- С. 1669 - 1673. |
2018 |
|
15 |
Kanatnikov A.N. New criteria of equilibrium points stability for discrete-time systems // Proceedings of 2018 14th International Conference Stability and Oscillations of Nonlinear Control Systems (Pyatnitskiys Conference), STAB 2018, 2018. |
2018 |
|
16 |
Kanatnikov A.N., Liu W., Tkachev S.B. Path Coordinates in a 3D Path Following Problem // Mathematical Models and Computer Simulations 2018 .- Vol. 10 , Issue 3 .- С. 265 - 275. |
2018 |
| 17 | Kanatnikov A.N. Stability of Equilibria of Discrete-Time Systems and Localization of Invariant Compact Sets // Differential Equations 2018 .- Vol. 54 , Issue 11 .- С. 1414 - 1418. |
2018 |
|
18 |
Kim S. On the generalization of Conway algebra // Journal of Knot Theory and Its Ramifications 2018 .- Vol. 27 , Issue 2 .- Art.no 1850014 |
2018 |
|
19 |
Kim S. The Groups G 2 n with Additional Structures // Mathematical Notes 2018 .- Vol. 103 , Issue 3-4 .- С. 593 - 609 |
2018 |
|
20 |
Kirillov A.A., Montani G, Savelova E.P. Strong standing gravitational wave in a closed Universe // Journal of Experimental and Theoretical Physics Letters (JETP Letters) 2018 .- Issue 6 , Vol. 107 .- С. 333 - 337. |
2018 |
| 21 | Kirillov A.A., Savelova E.P. Effects of Scattering of Radiation on Wormholes // Universe 2018 .- Vol.4, Issue 2 -Art.no 35. |
2018 |
| 22 | Kirillov A.A., Savelova E.P. On Modification of Newton's Law by a Homogeneous Distribution of Wormholes in Space // Gravitation and Cosmology 2018 .- Vol. 24 , Issue 4 .- С. 337 - 343. |
2018 |
| 23 | Kirillov A.A., Savelova E.P. On scattering of CMB radiation on wormholes: Kinematic SZ-effect // 14th Marcel Grossman Meeting On Recent Developments in Theoretical and Experimental General Relativity, Astrophysics and Relativistic Field Theories, Proceedings 2018 .- С. 2167 - 2172. |
2018 |
| 24 | Kirillov A.A., Savelova E.P. Origin of the logarithmic correction to the Newton’s law in the presence of a homogeneous gas of wormhole // 14th Marcel Grossman Meeting On Recent Developments in Theoretical and Experimental General Relativity, Astrophysics and Relativistic Field Theories, Proceedings 2018 .- No 14 .- С. 1481 - 1486. |
2018 |
| 25 | Kochetkov S.A., Krasnova S.A., Utkin A.V. Block design of electromechanical systems under parametric uncertainty and incomplete measurements // AIP Conference Proceedings 2018 .- Vol. 2046 .- Art.no 020049. |
2018 |
| 26 | Kochetkov S.A., Krasnova S.A., Utkin A.V. Robust Control for Synchronous Electric Drive Under Uncertainty Conditions // AIP Conference Proceedings 2018 .- Vol. 2046 .- Art.no 020047. |
2018 |
|
27 |
Krasnova S.A. Cascade design of disturbances observers for non-linear control plant of general form // Proceedings of 2018 14th International Conference Stability and Oscillations of Nonlinear Control Systems (Pyatnitskiys Conference), STAB 2018, 2018. |
2018 |
| 28 | Krasnova S.A. Cascade Synthesis of External Perturbations Observers Based on Virtual Models // 14th International Scientific-Technical Conference on Actual Problems of Electronic Instrument Engineering, APEIE 2018 - Proceedings 2018 .- С. 241 - 246 .- Art.no 8545125. |
2018 |
|
29 |
Krasnova S.A., Antipov A.S. Hierarchical Design of Sigmoidal Generalized Moments of Manipulator under Uncertainty // Automation and Remote Control 2018 .- Vol. 79 , Issue 3 .- С. 554 - 570. |
2018 |
|
30 |
Krishchenko A.P. Analysis of nonlinear sistems by the localization method // Proceedings of 2018 14th International Conference Stability and Oscillations of Nonlinear Control Systems (Pyatnitskiys Conference), STAB 2018. |
2018 |
|
31 |
Krishchenko A.P. Behavior of Trajectories in Localizing Sets // Doklady Mathematics 2018 .- Vol. 97 , No 3 .- С. 243 - 246. |
2018 |
| 32 | Krishchenko A.P. Behavior of Trajectories of Time-Invariant Systems // Differential Equations 2018 .- Vol. 54 , No 11 .- С. 1419 - 1424. |
2018 |
|
33 |
Krishchenko A.P., Starkov K.E. The four-dimensional Kirschner-Panetta type cancer model: How to obtain tumor eradication? // Mathematical Biosciences and Engineering 2018 .- Vol. 15 , Issue 5 .- С. 1243 - 1254. |
2018 |
|
34 |
Kulikova O.V. On Independent Families of Normal Subgroups in Free Groups // Journal of Mathematical Sciences (United States) 2018 .- Vol. 233 , Issue 1 .- С. 125 - 136. |
2018 |
|
35 |
Manturov V.O., Rushworth William Additional gradings on generalizations of Khovanov homology and invariants of embedded surfaces // Journal of Knot Theory and Its Ramifications 2018 .- Vol. 27 , Issue 9 .- Art.no 1842001. |
2018 |
|
36 |
Nefedov G. Time-scaling for increasing a relative degree of single-input single-output affine systems // Proceedings of 2018 14th International Conference Stability and Oscillations of Nonlinear Control Systems (Pyatnitskiys Conference), STAB 2018. |
2018 |
| 37 | Pankratov V.A., Barkin M.Yu. Determination of the satellite attitude motion according to the onboard measurements data // IOP Conference Series: Materials Science and Engineering 2018 .- Vol. 468 , Issue 1 .- Art.no 012026. |
2018 |
|
38 |
Reshmin S.A. The effect of loss of traction under asymmetric vibrations of the drive wheels of the vehicle // Proceedings of 2018 14th International Conference Stability and Oscillations of Nonlinear Control Systems (Pyatnitskiys Conference), STAB 2018. |
2018 |
|
39 |
Reshmin S.A. The Threshold Absolute Value of a Relay Control Bringing a Satellite to a Gravitationally Stable Position in Optimal Time // Doklady Physics 2018 .- Vol. 63 , Issue 6 .- С. 257 - 261. |
2018 |
| 40 | Reshmin S.A. Threshold Absolute Value of a Relay Control when Time-Optimally Bringing a Satellite to a Gravitationally Stable Position // Journal of Computer and Systems Sciences International 2018 .- Vol. 57 , Issue 5 .- С. 713 - 722. |
2018 |
| 41 | Seongjeong Kim, The Groups G2 n with Additional Structures // Mathematical Notes 2018 .- Vol. 103 , Issue 3-4 .- С. 593 - 609. |
2018 |
|
42 |
Shchigolev V.V., Stepanov D.A. Three-dimensional isolated quotient singularities in even characteristic // Glasgow Mathematical Journal 2018 .- Vol. 60 , Issue 2 .- С. 435 - 445. |
2018 |
|
43 |
Tchaikovsky M.M.,Timin V.N., Kustov A.Yu., Kurdyukov A.P. Numerical Procedures for Anisotropic Analysis of Time-Invariant Systems and Synthesis of Suboptimal Anisotropic Controllers and Filters // Automation and Remote Control 2018 .- Vol. 79 , Issue 1 .- С. 128 - 144. |
2018 |
| 44 | Utkin A.V., Krasnova S.A. Decomposition Principle in the Problem of Synthesis of State Observers for SISO Systems under the Action of External Disturbances // 14th International Scientific-Technical Conference on Actual Problems of Electronic Instrument Engineering, APEIE 2018 - Proceedings 2018 .- С. 284 - 289 .- Art.no 8545938. |
2018 |
|
45 |
Volkov B.O. Levy Laplacians in Hida Calculus and Malliavin Calculus // Proceedings of the Steklov Institute of Mathematics 2018 .- Vol. 301 , Issue 1 .- С. 11 - 24. |
2018 |
| 46 | Volkov B.O. Levy Laplacians and annihilation process // Ученые записки Казанского университета. Серия: Физико-математические науки 2018 .- Т. 160 , № 2 .- С. 399 - 409. |
2018 |
| 47 | Yurchenkov A.V. On the Control Design for Linear Time–Invariant Systems with Moments Constraints of Disturbances in Anisotropy–based Theory // IFAC-PapersOnLine. 2018. V. 51, № 32. С. 160-165. | 2018 |
| 48 | Yurchenkov A.V. Anisotropy-Based Controller Design for Linear Discrete-Time Systems with Multiplicative Noise // Journal of Computer and Systems Sciences International, 2018, Vol. 57, No. 6, pp. 864–873. | 2018 |
|
Статьи в журналах/сборниках из перечня ВАК, РИНЦ
|
||
| 1 | Аттетков А.В., Волков И.К., Гайдаенко К.А. Автомодельные процессы теплопереноса в прозрачном для излучения твердом теле с поглощающим включением при наличии фазовых превращений в системе // Вестник МГТУ им.Н.Э.Баумана. Серия "Машиностроение" 2019 .- № 2 .- С. 60 - 70. | 2019 |
| 2 | Аттетков А.В., Волков И.К. Температурное поле разделяющей две различные среды изотропной стенки, обладающей анизотропным покрытием, при его локальном нагреве в условиях теплообмена с внешней средой // Тепловые процессы в технике 2019 .- Т. 11 , № 2 .- С. 86 - 96. | 2019 |
| 3 | Бахтиярова О.Н., Глушаченков А.А., Казаков В.Ю., Шарыкина О.В. Методический подход к обоснованию рационального способа защиты населения от поражающих факторов при применении обычных средств поражения // Научные и образовательные проблемы гражданской защиты 2019 .- № 1(40) .- С. 19 - 24. | 2019 |
| 4 | Бахтиярова О.Н., Глушаченков А.А., Казаков В.Ю., Смирнов Б.П. Обоснование рационального выбора жилых зданий и комплектов защитных экранов для защиты населения от поражающих факторов при применении обычных средств поражения // Научные и образовательные проблемы гражданской защиты 2019 .- № 1(40) .- С. 33 - 39. | 2019 |
| 5 | Бородина Ю.В. Легкотестируемые схемы в базисе Жегалкина при константных неисправностях типа "1" на выходах элементов // Дискретная математика 2019 .- Т. 31 , Вып. 2 .- С. 14 - 19. | 2019 |
| 6 | Бузаверов К.А., Гресс М.А., Рыжова М.Ю., Шебешев К.И. Упрочняющая термическая обработка экономно легированной стали после цементации // Вестник научно-технического развития 2019 .- № 2(138) .- С. 3 - 8. | 2019 |
| 7 | Горяинов В.Б., Горяинова Е.Р. Сравнительный анализ робастных и классических методов оценивания параметров уравнения пороговой авторегрессии // Автоматика и телемеханика 2019 .- № 4 .- С. 93 - 104. | 2019 |
| 8 | Грибов А.Ф., Шахтарин Б.И. Построение решений кусочно-линейных систем // Научный вестник Московского государственного технического университета гражданской авиации 2019 .- Т. 22 , № 1 .- С. 106 - 123. | 2019 |
| 9 | Грибов А.Ф., Шахтарин Б.И. Построение решений кусочно-линейных фазовых систем // Научный вестник Московского государственного технического университета гражданской авиации 2019 .- Т. 22 , № 1 .- С. 106 - 123. | 2019 |
| 10 | Косова А.В., Ласковая Т.А. Методические аспекты изложения теории в курсе высшей математики // Научно-методический электронный журнал Концепт 2019 .- № V2 .- С. 1 - 7. | 2019 |
| 11 | Пахомова С.А., Помельникова А.С., Рыжова М.Ю., Симич-Лафицкая Е.М. Повышение качества автомобильных сталей // Все материалы. Энциклопедический справочник. 2019 .- № 8 .- С. 25 - 30. | 2019 |
| 12 | Пелевина И.Н., Ласковая Т.А., Ахметова Ф.Х. Методические аспекты изложения темы "Преобразование Лапласа. Нахождение изображения по оригиналу" // Научно-методический электронный журнал Концепт 2019 .- № 1 .- С. 1 - 6. | 2019 |
| 13 | Попова Е.М., Чигирёва О.Ю. Методика изложения темы "Применение степенных рядов для приближенного вычисления определенных интегралов" // Научно-методический электронный журнал Концепт 2019 .- № 6. | 2019 |
| 14 | Попова Е.М., Косова А.В. Методические особенности изложения темы "Решение задачи Коши методом включения начальных условий в мгновенно действующие источники" // Научно-методический электронный журнал Концепт 2019 .- № V3. | 2019 |
| 15 | Решмин С.А. Анализ условий потери тяги транспортного средства при интенсивном старте // Известия Российской академии наук. Теория и системы управления 2019 .- № 3 .- С. 24 - 33. | 2019 |
| 16 | Решмин С.А. Качественный анализ нежелательного эффекта потери силы тяги транспортного средства во время интенсивного старта // Доклады Академии наук 2019 .- Т. 484 , № 3 .- С. 289 - 29. | 2019 |
| 17 | Смирнов А.Е., Фахуртдинов Р.С., Рыжова М.Ю., Пахомова С.А. Технологические особенности вакуумной цементации низколегированных сталей // Проблемы машиностроения и надежности машин, 2019 .- №2 .- С. 84 - 90. | 2019 |
| 18 | Тимин В.Н., Кустов А.Ю., Курдюков А.П., Гольдин Д.А., Вершинин Ю.А. Субоптимальная анизотропийная фильтрация для линейных дискретных нестационарных систем с нецентрированным внешним возмущением // Автоматика и телемеханика 2019 .- № 1 .- С. 3 - 20. | 2019 |
|
1 |
Аттетков А.В., Волков И.К. Влияние анизотропии свойств на оптимальную толщину покрытия охлаждаемой пластины при локальном тепловом воздействии // Известия Российской академии наук. Энергетика 2018 .- № 1.- С. 78 - 86. |
2018 |
|
2 |
Аттетков А.В., Волков И.К. Оптимальная толщина анизотропного покрытия разделительной стенки двух различных сред при локальном тепловом воздействии // Вестник МГТУ им.Н.Э.Баумана. Серия "Машиностроение" 2018 .- № 4 .- С. 4 - 15. |
2018 |
|
3 |
Аттетков А.В., Волков И.К. Температурное поле анизотропного полупространства при его локальном нагреве в условиях теплообмена с внешней средой // Вестник МГТУ им.Н.Э.Баумана. Серия "Естественные науки" 2018 .- № 3 .- С. 4 - 12. |
2018 |
|
4 |
Аттетков А.В., Волков И.К. Температурное поле анизотропного полупространства, подвижная граница которого подвержена локальному импульсно-периодическому тепловому воздействию в условиях теплообмена с внешней средой // Математика и математическое моделирование 2018 .- № 2 .- С. 19 - 32. |
2018 |
|
5 |
Аттетков А.В, Власов П.А., Волков И.К. Условие существования оптимальной толщины охлаждаемой анизотропной стенки, подверженной локальному тепловому воздействию // Теплофизика высоких температур 2018 .- Т. 56 , № 3 .- С. 407 - 411. |
2018 |
|
6 |
Ахметова Ф.Х., Головина А.М. Метод разбиения функции на отдельные уравнения при построении графиков многозначных линейных функций, содержащих знак модуля // Научно-методический электронный журнал Концепт 2018 .- № V9 .- С. 76 - 81. |
2018 |
| 7 | Ахметова Ф.Х., Головина А.М. Метод разбиения плоскости на несколько областей при построении графиков многозначных линейных функций, содержащих знак модуля // Научно-методический электронный журнал Концепт 2018 .- № V12. |
2018 |
| 8 | Ахметова Ф.Х., Чигирёва О.Ю. Методика изложения темы "Решение краевых задач для уравнения Лапласа для круга и кольца методом разделения переменных" // Научно-методический электронный журнал Концепт 2018 .- № V10 .- С. 23 - 32. |
2018 |
| 9 | Ахметова Ф.Х., Головина А.М. Построение графиков многозначных линейных функций, содержащих знак модуля // Научно-методический электронный журнал Концепт 2018 .- № V11 .- С. 6 - 11. |
2018 |
| 10 | Бахтиярова О.Н. Методика расчета скорости распространения пожара с учетом влияния скорости ветра и рельефа местности // Научные и образовательные проблемы гражданской защиты 2018 .- № 1 (36) .- С. 62 - 68. |
2018 |
| 11 | Бахтиярова О.Н. Сравнительный анализ результатов детерминированного и стохастического подходов к планированию аварийно-спасательных работ // Технологии гражданской безопасности 2018 .- Т. 15 , № 2 (56) .- С. 70 - 74. |
2018 |
|
12 |
Беднов Б.Б., Бородин П.А., Чеснокова К.В. Существование липшицевых выборок из точек Штейнера // Математический сборник 2018 .- Т. 209 , № 2 .- С. 3 - 21. |
2018 |
|
13 |
Белинская И.С., Четвериков В.Н. Метод накрытий для терминального управления и орбитальная декомпозиция систем // Дифференциальные уравнения 2018 .- Т. 54 , № 4 .- С. 502 - 513. |
2018 |
|
14 |
Белоусов А.И. О некоторых свойствах полуколец // Машиностроение и компьютерные технологии 2018 .- № 3. |
2018 |
|
15 |
Белоусов А.И., Исмагилов Р.С. Об одном достаточном условии нерегулярности языков // Математика и математическое моделирование 2018 .- № 4 .- С. 1 - 11. |
2018 |
|
16 |
Вергазова О.Б. Геометрический и физический аспекты понятия непрерывности функции в курсе математического анализа // Научно-методический электронный журнал Концепт 2018 .- № V1 .- С. 53 - 58. |
2018 |
| 17 | Вергазова О.Б. Организация внеаудиторной работы студентов при изучении отдельных тем курса "Численные методы" // Научно-методический электронный журнал Концепт 2018 .- № V11 .- С. 18 - 23. |
2018 |
| 18 | Виноградова М.С., Ткачёв С.Б., Ткачёва О.С. Применение наблюдателя в скользящем режиме при моделировании процесса антиангиогенной терапии // Математика и математическое моделирование 2018 .- № 6 .- С. 52 - 71. |
2018 |
|
19 |
Волков Б.О. Лапласианы Леви в исчислении Хиды и исчислении Маллявэна // Труды Математического института им. В.А. Стеклова РАН 2018 .- Т. 301 .- С. 18 - 32. |
2018 |
|
20 |
Горяиноа А.В., Горяинов В.Б. М-оценки параметров процесса авторегрессии со случайными коэффициентами // Автоматика и телемеханика 2018 .- № 8 .- С. 50 - 65. |
2018 |
|
21 |
Горяинов В.Б., Горяинова Е.Р. М-оценки в пороговой авторегрессии // Вестник МГТУ им.Н.Э.Баумана. Серия "Естественные науки" 2018 .- № 3 .- С. 13 - 23. |
2018 |
|
22 |
Граник И.С., Грибов А.Ф. Об одном решении нелинейного параболического уравнения с нестационарным показателем нелинейности // Вестник МГТУ им.Н.Э.Баумана. Серия "Естественные науки" 2018.- № 4 .- С. 4 - 13. |
2018 |
|
23 |
Грибов А.Ф. Локализация инвариантных компактов в многомерных системах с фазовым управлением // Автоматика и телемеханика 2018 .- № 8 .- С. 27 - 37. |
2018 |
|
24 |
Грибов А.Ф., Цисарский А.Д., Шахтарин Б.И. Непрерывные системы фазовой синхронизации с кусочно-линейными функциями // Радиотехника 2018 .- № 7 .- С. 119 - 128. |
2018 |
|
25 |
Ефремова С.Н., Косова А.Н., Ласковая Т.А. Методические аспекты изложения темы «Линейные дифференциальные уравнения с постоянными коэффициентами и правой частью специального вида» в курсе «Дифференциальные уравнения» // Научно-методический электронный журнал Концепт 2018.- № V3 .- С. 8 - 17. |
2018 |
| 26 | Иванков П.Л., Обухов В.П. О разложении элементарных функций в степенные ряды // Инженерный вестник 2018 .- № 3. |
2018 |
| 27 | Ильин А.В., Фурсов А.С., Мальцева А.В. Обобщение метода внутренней аппроксимации для решения задачи одновременной стабилизации // Дифференциальные уравнения 2018 .- Т. 54 , № 12 .- С. 1710 - 1713. |
2018 |
| 28 | Ильин С.С., Лукин В.В., Шумилов Ю.Ю. Методика численной оптимизации расположения спутников связи на орбитах // Препринты ИПМ им. М.В. Келдыша 2018 .- № 199 .- С. 1 - 23. |
2018 |
| 29 | Кавинов А.В. О вычислении первых интегралов систем ОДУ третьего порядка // Математика и математическое моделирование 2018 .- № 6 .- С. 11 - 12. |
2018 |
| 30 | Канатников А.Н. Устойчивость положений равновесия дискретных систем и локализация инвариантных компактов // Дифференциальные уравнения 2018 .- Т. 54 , № 11 .- С. 1440 - 1444. |
2018 |
|
31 |
Кандаурова И.Е. Общая схема вычисления рядов с положительными членами // Машиностроение и компьютерные технологии 2018 .- № 4 |
2018 |
|
32 |
Ким С. Группы G 2n с дополнительными структурами // Математические заметки 2018 .- Т. 103 , № 4 .- С. 549 - 567. |
2018 |
|
33 |
Кириллов А.А., Савелова Е.П., Монтани Дж. О структуре интенсивной стоячей гравитационной волны // Письма в Журнал экспериментальной и теоретической физики 2018 .- Т. 107 , № 6 .- С. 349 - 352. |
2018 |
|
34 |
Косова А.В. Методические аспекты изложения темы "Дифференциальные уравнения первого порядка" в курсе "Дифференциальные уравнения" // Научно-методический электронный журнал Концепт 2018.- № V9. - С. 13 - 22. |
2018 |
| 35 | Краснова С.А. Оценивание внешних возмущений на основе виртуальных динамических моделей // Управление большими системами: сборник трудов (электронный журнал) 2018 .- Вып. 76 .- С. 6 - 25. |
2018 |
|
36 |
Крищенко А.П. Поведение траекторий в локализирующих множествах // Доклады Академии наук 2018 .- Т. 480 , № 4 .- С. 393 - 396. |
2018 |
| 37 | Крищенко А.П. Поведение траекторий автономных систем // Дифференциальные уравнения 2018 .- Т. 54 , № 11 .- С. 1445 - 1450 |
2018 |
| 38 | Кулешов А.В., Фатеев В.В., Тверская Е.С. Маховичный индикаторный гиростабилизатор с ограничением в канале стабилизации // Авиакосмическое приборостроение 2018 .- № 11 .- С. 3 - 9. |
2018 |
| 39 | Лю Вей Методы планирования пути в среде с препятствиями (обзор) // Математика и математическое моделирование 2018 .- № 1 .- С. 33 - 52. |
2018 |
|
40 |
Пахомова С.А., Рыжова М.Ю. Эффективность деформационного упрочнения цементованных зубчатых колес из стали 13Х3НВМ2Ф-Ш // Вестник МГТУ им.Н.Э.Баумана. Серия "Машиностроение" 2018 .- № 1 .- С. 66 - 74. |
2018 |
|
41 |
Попова Е.М., Чигирева О.Ю. Методические особенности изложения темы "Обобщенные функции. Обобщенные производные. Дельта-функция Дирака" // Научно-методический электронный журнал Концепт 2018.- № V7.- С. 54 - 62. |
2018 |
| 42 | Попова Е.М., Чигирева О.Ю. Методика изложения темы "Решение краевых задач для уравнения Лапласа в прямоугольнике методом Фурье" // Научно-методический электронный журнал Концепт 2018 .- № 9. |
2018 |
| 43 | Птицына И.В., Птицына Е.В. О некоторых проблемах исследовательской деятельности школьников при выполнении межпредметных исследований // Вестник Московского государственного областного университета. Серия: Педагогика 2018 .- № 4 .- С. 39 - 48. |
2018 |
|
44 |
Решмин С.А. Пороговая абсолютная величина релейного управления при наискорейшем приведении спутника в гравитационно-устойчивое положение // Доклады Академии наук 2018 .- Т. 480 , № 6 .- С. 671 - 675. |
2018 |
|
45 |
Смирнов А.Е., Фахуртдинов Р.С., Рыжова М.Ю., Пахомова С.А. Определение режимов вакуумной цементации на основе расчетного метода // Упрочняющие технологии и покрытия 2018 .- Т. 14 , № 6 .- С. 269 - 274. |
2018 |
|
46 |
Стырт О.Г. Топологические и гомологические свойства пространства орбит компактной линейной группы Ли с коммутативной связной компонентой // Вестник МГТУ им.Н.Э.Баумана. Серия "Естественные науки" 2018 .- № 3 .- С. 68 - 81. |
2018 |
| 47 | Стырт О.Г. Топологические и гомологические свойства пространства орбит компактной линейной группы Ли с коммутативной связной компонентой. Выводы // Вестник МГТУ им.Н.Э.Баумана. Серия "Естественные науки" 2018 .- № 6 .- С. 48 - 63. |
2018 |
| 48 | Фетисов Д.А. А-орбитальная линеаризация аффинных систем // Дифференциальные уравнения 2018 .- Т. 54 , № 11 .- С. 1518 - 1532. |
2018 |
|
49 |
Фурсов А.С., Миняев С.И., Гусева В.С. Построение цифрового стабилизатора для переключаемой линейной системы с запаздыванием в управлении // Дифференциальные уравнения 2018 .- Т. 54 , № 8 .- С. 1132 - 1141. |
2018 |
| 50 |
Фурсов А.С., Емельянов С.В., Капалин И.В., Сагадинова Е.С. Стабилизация векторных по входу переключаемых линейных систем с режимами различных динамических порядков // Дифференциальные уравнения
2018 .- Т. 54 , № 11 .- С. 1540 - 1546.
|
2018 |
|
51 |
Чайковский М.М., Тимин В.Н., Кустов А.Ю, Курдюков А.П. Численные процедуры анизотропийного анализа стационарных систем и синтеза субоптимальных анизотропийных регуляторов и фильтров // Автоматика и телемеханика 2018 .- № 1 .- С. 162 - 182. |
2018 |
| 52 | Чайковскай М.М., Курдюков А.П. Анизотропийное субоптимальное управление для систем с дробно-линейной неопределенностью // Автоматика и телемеханика 2018 .- № 6 .- С. 172 - 190. |
2018 |
|
53 |
Четвериков В.Н. Построение обратимых отображений вход-выход и параметрическая идентификация // Дифференциальные уравнения 2018 .- Т. 54 , № 11 .- С. 1547 - 1556. |
2018 |
| 54 | Четвериков В.Н. Представление обратимых линейных обыкновенных дифференциальных операторов в виде композиции простейших операторов // Математика и математическое моделирование 2018 .- № 4 .- С. 45 - 61. |
2018 |
|
55 |
Шебешев К.И., Бузаверов К.А., Рыжова М.Ю., Гресс М.А. Повышение контактной выносливости зубчатых колес из стали 25Х13Н2 // Вестник научно-технического развития 2018 .- № 6 (130) .- С. 10 - 15. |
2018 |
| 56 | Юрченков А.В. Синтез анизотропийного управления для линейной дискретной системы с мультипликативными шумами // Известия Российской академии наук. Теория и системы управления 2018 .- № 6 .- С. 33 - 44. |
2018 |
|
Доклады
|
||
|
1 |
Антипов А.С., Краснова С.А. Декомпозиционыый синтез инвариантных систем с нелинейными локальными связями // Материалы XIV Международной научной конференции Устойчивость и колебания нелинейных систем управления. - М: ИПУ РАН, 2018. - С. 36-39. |
2018 |
|
2 |
Глазков Т.В., Голубев А.Е. Управление движением квадрокоптера в горизонтальной плоскости // Материалы XIV Международной научной конференции Устойчивость и колебания нелинейных систем управления. - М: ИПУ РАН, 2018. - С. 108-111. |
2018 |
|
3 |
Канатников А.Н. Новые критерии устойчивости положений равновесия для систем дискретного времени // Материалы XIV Международной научной конференции Устойчивость и колебания нелинейных систем управления. - М: ИПУ РАН, 2018. - С. 197-200. |
2018 |
|
4 |
Краснова С.А. Каскадный синтез наблюдателей внешних возмущений для нелинейных объектов управления общего вида // Материалы XIV Международной научной конференции Устойчивость и колебания нелинейных систем управления. - М: ИПУ РАН, 2018. - С. 237-240. |
2018 |
|
5 |
Крищенко А.П. Исследование нелинейных систем методом локализации // Материалы XIV Международной научной конференции Устойчивость и колебания нелинейных систем управления. - М: ИПУ РАН, 2018. - С. 241-244. |
2018 |
|
6 |
Нефедов Г.А. Анализ влияния замены независимой переменной на относительную степень аффинной системы со скалярным выходом // Материалы XIV Международной научной конференции Устойчивость и колебания нелинейных систем управления. - М: ИПУ РАН, 2018. - С. 305-307. |
2018 |
|
7 |
Решмин С.А. Решмин А.И. Моделирование движения колеса с пневматиком с проскальзыванием и отрывом // Материалы XIV Международной научной конференции Устойчивость и колебания нелинейных систем управления. - М: ИПУ РАН, 2018. - С. 356-359. |
2018 |
|
8 |
Решмин С.А. Эффект тяги при несимметричных колебаниях ведущих колес ТС // Материалы XIV Международной научной конференции Устойчивость и колебания нелинейных систем управления. - М: ИПУ РАН, 2018. - С. 359-362. |
2018 |
|
9 |
Тимин В.Н., Юрченков А.В. Субоптимальные анизотропийные регуляторы для стационарных систем при дополнительных ограничениях на первый и второй моменты внешнего возмущения // Материалы XIV Международной научной конференции Устойчивость и колебания нелинейных систем управления. - М: ИПУ РАН, 2018. - С. 429-432. |
2018 |
|
10 |
Фетисов Д.А. Условие орбитальной линеаризуемости аффинных систем со скалярным управлением // Материалы XIV Международной научной конференции Устойчивость и колебания нелинейных систем управления. - М: ИПУ РАН, 2018. - С. 455-458. |
2018 |
|
11 |
Чайковский М.М., Курдюков А.П. Решение задачи анизотропийной субоптимальной фильтрации для системы с неопределенностью // Материалы XIV Международной научной конференции Устойчивость и колебания нелинейных систем управления. - М: ИПУ РАН, 2018. - С. 476-479. |
2018 |
|
12 |
Юрченков А.В. Качество систем с мультипликативными шумами в рамках анизотропийной теории управления // Материалы XIV Международной научной конференции Устойчивость и колебания нелинейных систем управления. - М: ИПУ РАН, 2018. - С. 492-495. |
2018 |
- Details
- Category: Научная работа
Программный комплекс «КОКОН»
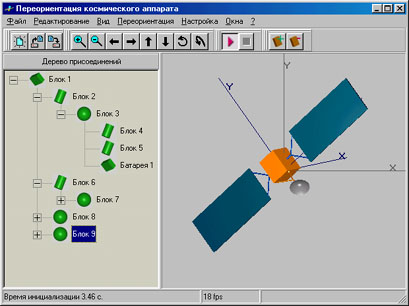
Разработанный НУК ФН МГТУ им. Н.Э. Баумана программный комплекс «КОсмический КОНструктор» предназначен для
- визуального конструирования объёмных моделей космических станций и аппаратов;
- вычисления инерционно-массовых характеристик космической станции по известным характеристикам отдельных элементов конструкции;
- моделирования процесса переориентации космического аппарата и визуализации угловых движений КА под воздействием управления;
- сравнения эффективности различных алгоритмов управления угловым положением КА.
Программа обладает развитым интуитивным пользовательским интерфейсом. Процесс конструирования разделён на два этапа: сборку модулей из простейших геометрических конструкций - примитивов и присоединение модулей друг к другу.
- Details
- Category: Научная работа
На кафедре осуществляется подготовка аспирантов по следующим специальностям:
| Код | Наименование |
|---|---|
| 05.13.01 | Системный анализ, управление и обработка информации |
| 05.13.18 | Математическое моделирование, численные методы и комплексы программ |
В аспирантуру МГТУ им. Н.Э. Баумана на конкурсной основе принимаются граждане Российской Федерации, имеющие законченное профессиональное высшее образование. Граждане иностранных государств, включая граждан государств участников СНГ, принимаются в аспирантуру на платной договорной основе. Приём заявлений проводится с 1 июня по 10 сентября. Поступающие в аспирантуру проходят обязательное собеседование с предполагаемым научным руководителем, представляют реферат по направлению будущей диссертации и сдают конкурсные вступительные экзамены по специальности, философии, одному из иностранных языков. Приём экзаменов проводится в период с 20 сентября по 10 октября. Лица, сдавшие какие-либо кандидатские экзамены, при поступлении в аспирантуру освобождаются от сдачи соответствующих вступительных экзаменов. Зачисление в аспирантуру производится с 20 октября приказом ректора в соответствии с планом приёма аспирантов. Приёмная комиссия выносит мотивированное решение по каждому кандидату на основании заключения предполагаемого научного руководителя, заведующего кафедрой и результатов конкурсных экзаменов.
Приём заявлений проводится с 1 июня по 10 сентября. Заявление о приёме в аспирантуру подаётся на имя ректора с приложением:
- личного листка по учёту кадров (бланк можно получить в отделе аспирантуры);
- копии диплома об окончании ВУЗа;
- копии приложения к диплому;
- 3-х фотокарточек размером 3x4;
- отзыва на реферат по избранной специальности.
Бланк заявления выдаётся в отделе аспирантуры. Диплом ВУЗа и паспорт предъявляются лично.
Приём экзаменов проводится в период с 20 сентября по 10 октября. Результаты вступительных экзаменов действительны в течении календарного года. Пересдача экзаменов не допускается.
-
Основные сведения о математических моделях
- Математические модели объектов, микро-, макро- и метамодели.
- Методы построения математических моделей.
- Основные понятия и имитационного и статистического моделирования.
-
Математический аппарат моделирования
-
Алгебра и геометрия
- Множества, подмножества и операции над ними.
- Множество действительных чисел. Числовая прямая.
- Отображения множеств.
- Неподвижная точка отображения.
- Мощность множества.
- Кортеж.
- Элементы комбинаторики.
- Декартово произведение.
- Соответствия и бинарные отношения.
- Операции над соответствиями.
- Свойства бинарных отношений.
- Отношения эквивалентности.
- Упорядоченные множества.
- Мощность множества.
- Высказывания и их истинность.
- Операции над высказываниями их свойства.
- Основные законы композиции и алгебраические структуры.
- Группы и кольца.
- Группа подстановок.
- Кольцо многочленов.
- Группоиды, полугруппы.
- Циклические группы.
- Тела, поля.
- Поле комплексных чисел.
- Векторные и скалярные величины.
- Линейные операции над векторами и их свойства.
- Ортогональная проекция.
- Линейная зависимость и независимость векторов.
- Базис.
- Вычисления в координатах.
- Скалярное, векторное и смешанное произведения векторов, и их свойства.
- Декартова система координат.
- Преобразование прямоугольных координат.
- Простейшие задачи аналитической геометрии.
- Вычисление площадей и объемов.
- Кривые и поверхности.
- Полярная система координат.
- Цилиндрическая и сферическая системы координат.
- Прямая на плоскости.
- Алгебраические кривые первого порядка.
- Специальные виды уравнения прямой.
- Взаимное расположение двух прямых.
- Расстояние от точки до прямой.
- Прямая и плоскость в пространстве.
- Алгебраические поверхности первого порядка.
- Специальные виды уравнения плоскости.
- Уравнения прямой в пространстве.
- Взаимное расположение прямых и плоскостей.
- Расстояние до плоскости и до прямой.
- Пучки и связки.
- Матрицы и операции над ними, их свойства.
- Блочные матрицы.
- Прямая сумма матриц
- Линейная зависимость строк и столбцов матриц.
- Элементарные преобразования матриц.
- Определители n-го порядка, их свойства.
- Методы вычисления определителей.
- Обратная матрица и ранг матрицы, их вычисление и свойства.
- Решение матричных уравнений.
- Теорема о базисном миноре.
- Системы линейных алгебраических уравнений.
- Формы записи СЛАУ.
- Критерий совместности СЛАУ.
- Формулы Крамера.
- Свойства решений однородных и неоднородных систем.
- Методы решения СЛАУ.
- СЛАУ с комплексными коэффициентами.
- Линейные пространства.
- Базис и размерность линейного пространства.
- Преобразование координат вектора при замене базиса.
- Линейные подпространства, их свойства.
- Ранг системы векторов.
- Линейные оболочки и системы уравнений.
- Прямое дополнение.
- Евклидовы пространства.
- Неравенство Коши - Буняковского.
- Нормированные пространства.
- Ортогональные системы векторов и их свойства.
- Ортогональные и ортонормированные базисы.
- Вычисления в ортонормированном базисе.
- Процесс ортогонализации Грама - Шмидта.
- Ортогональное дополнение.
- Нормы матриц и их свойства.
- Метод наименьших квадратов.
- Псевдорешения систем линейных уравнений и псевдообратная матрица.
- Линейные операторы.
- Изоморфизм линейных пространств.
- Матрица линейного оператора и ее свойства.
- Собственные векторы и собственные значения.
- Характеристическое уравнение матрицы и линейного оператора.
- Свойства собственных векторов.
- Теорема Гамильтона - Кэли.
- Сопряженный оператор.
- Самосопряженные операторы и их матрицы.
- Свойства собственных векторов самосопряженного оператора.
- Ортогональные матрицы и операторы, их свойства.
- Матрицы перехода в евклидовом пространстве.
- Приведение симметрической матрицы к диагональному виду.
- Квадратичные формы, их преобразование.
- Квадратичные формы канонического вида.
- Ортогональные преобразования квадратичных форм.
- Закон инерции.
- Критерий Сильвестра.
- Кривые второго порядка, их канонические и полярные уравнения.
- Поверхность вращения и преобразование сжатия.
- Поверхности второго порядка.
- Цилиндрические поверхности.
- Метод сечений.
- Конические и линейчатые поверхности.
- Конические сечения.
- Упрощение уравнений кривых и поверхностей второго порядка.
- Классификация кривых и поверхностей второго порядка.
- Элементы тензорной алгебры.
- Сопряженное пространство.
- Полилинейные формы.
- Тензоры.
- Операции c тензорами.
- Численные методы решения СЛАУ.
- Прямые и итерационные методы решения СЛАУ.
- Метод Гаусса и его особенности.
- Метод прогонки.
- Мультипликативные разложения матриц.
- QR-разложение.
- Сингулярное разложение.
- Обусловленность квадратных матриц.
- Итерационные методы, их каноническая форма записи.
- Методы Якоби, Зейделя, простой итерации, Ричардсона и релаксации.
- Сходимость итерационных методов.
- Теорема Самарского.
- Скорость сходимости стационарных итерационных методов.
-
Дифференциальное исчисление
- Метрические пространства и их непрерывные отображения.
- Окрестности в метрическом пространстве.
- Характерные точки множеств.
- Открытые, замкнутые и компактные множества.
- Свойства непрерывного отображения множеств.
- Линейно связные множества.
- Равномерная непрерывность.
- Предел отображения метрических пространств, его свойства и признаки существования.
- Полное метрическое пространство.
- Принцип сжимающих отображений.
- Действительные функции действительного переменного
- Функция и ее график.
- Способы задания функции.
- Основные элементарные функции.
- Числовые последовательности, их пределы.
- Свойства сходящихся последовательностей.
- Признаки существования предела последовательности.
-
Число
e .
- Предел функции в точке и его свойства.
- Односторонние пределы.
- Признаки существования предела.
- Свойства функций, имеющих конечный предел.
- Бесконечно малые и бесконечно большие функции.
- Предел сложной функции.
- Два замечательных предела.
- Экспонента, натуральные логарифмы и гиперболические функции.
- Непрерывность функции в точке, свойства функций, непрерывных в точке.
- Односторонняя непрерывность. Точки разрыва.
- Свойства функций, непрерывных в промежутке.
- Непрерывность основных элементарных функций.
- Непрерывность и разрывы монотонной функции.
- Асимптотическое поведение функций.
- Сравнение бесконечно малых функций.
- Эквивалентные бесконечно малые функции.
- Главная часть бесконечно малой функции.
- Сравнение бесконечно больших функций.
- Асимптоты графика функции.
- Производная функции ее механический и геометрический смысл.
- Касательная и нормаль к плоской кривой.
- Производные основных элементарных функций.
- Односторонние конечные и бесконечные производные.
- Дифференцируемость функции.
- Непрерывность дифференцируемой функции.
- Правила дифференцирования функций.
- Производная сложной и обратной функции.
- Производная функции, заданной параметрически.
- Дифференцирование неявных функций.
- Дифференциал и его геометрический смысл.
- Дифференциал сложной функции.
- Инвариантность формы записи дифференциала.
- Использование дифференциала в приближенных вычислениях.
- Производные и дифференциалы высших порядков.
- Основные теоремы дифференциального исчисления.
- Теорема Лагранжа и формула конечных приращений.
- Теорема Коши.
- Правило Бернулли - Лопиталя.
- Многочлен Тейлора и формула Тейлора.
- Различные представления остаточного члена формулы Тейлора.
- Формула Маклорена.
- Вычисление пределов при помощи формулы Тейлора.
- Использование формулы Тейлора в приближенных вычислениях.
- Условия возрастания и убывания функций.
- Экстремум функции.
- Необходимые и достаточные условия существования экстремума.
- Наибольшее и наименьшее значения функции в промежутке.
- Условия выпуклости функции.
- Точки перегиба.
- Общая схема исследования функции и построение ее графика.
- Особенности исследования функций, заданных параметрически.
- Векторная функция скалярного аргумента.
- Плоские кривые.
- Кривизна плоской кривой.
- Эволюта и эвольвента плоской кривой.
- Кривизна и кручение пространственной кривой.
- Формулы Френе.
- Интерполирование и численное дифференцирование.
- Линейная интерполяция.
- Квадратичная интерполяция.
- Интерполяционный многочлен Лагранжа.
- Интерполяционный многочлен Ньютона.
- Интерполирование с кратными узлами.
- Численное дифференцирование.
- Интерполирование сплайнами.
- Решение нелинейных уравнений.
- Отделение корней алгебраических уравнений.
- Численные методы уточнения значения корня.
- Метод простой итерации.
- Метод Ньютона.
- Комбинированные методы.
- Функции многих переменных
- Предел и непрерывность функции многих переменных.
- Линии и поверхности разрыва.
- Непрерывность по части переменных.
- Свойства функций многих переменных, непрерывных на компактах.
- Частные производные и их геометрическая интерпретация.
- Необходимые и достаточные условия дифференцируемости ФМП.
- Дифференцируемость сложной функции.
- Дифференциал функции многих переменных.
- Производные и дифференциалы высших порядков.
- Формула Тейлора.
- Дифференциалы в приближенных вычислениях.
- Теоремы о неявной и обратной функциях.
- Производная по направлению.
- Градиент.
- Касательная плоскость и нормаль.
- Касательная и нормаль к кривой на плоскости.
- Экстремум функции многих переменных.
- Необходимое и достаточное условия экстремума.
- Исследование функций на экстремум.
- Условный экстремум.
- Необходимое и достаточное условия условного экстремума.
- Нахождение наибольшего и наименьшего значений.
- Численные методы решения систем нелинейных уравнений.
- Итерационные методы решения.
- Метод Ньютона.
- Проблема глобальной сходимости.
- Интерполирование функций многих переменных.
- Интерполяционные сплайны первой степени.
- Билинейные интерполяционные сплайны.
- Бикубические сплайны двух переменных.
- Приближение кривых и поверхностей.
-
Интегральное исчисление
Интегральное исчисление функций одного действительного переменного
- Неопределенный интеграл.
- Первообразная и неопределенный интеграл, их свойства.
- Интегрирование подстановкой и заменой переменного, интегрирование по частям.
- Интегрирование рациональных дробей.
- Методы интегрирования иррациональных выражений.
- Определенный интеграл.
- Суммы и интегралы Дарбу.
- Критерий существования определенного интеграла.
- Классы интегрируемых функций.
- Свойства интегрируемых функций.
- Основные свойства определенного интеграла.
- Теоремы о среднем значении для определенного интеграла.
- Определенный интеграл с переменным пределом и его всойства.
- Несобственные интегралы.
- Интегралы по бесконечному промежутку и от неограниченных функций, их
- свойства.
- Абсолютная и условная сходимость несобственных интегралов.
- Признаки сходимости несобственных интегралов.
- Интегралы, зависящие от параметра.
- Дифференцирование и интегрирование интегралов по параметру.
- Равномерная сходимость несобственных интегралов.
- Признаки равномерной сходимости несобственных интегралов.
- Непрерывность и дифференцируемость несобственных интегралов по параметру.
- Интегрирование несобственных интегралов по параметру.
- Эйлеровы интегралы.
- Приложения определенного интеграла.
- Длина кривой.
- Площадь плоской фигуры.
- Объем тела.
- Площадь поверхности.
- Вычисление масс и моментов инерции.
- Статические моменты и координаты центра масс.
- Работа, энергия, сила давления.
- Численное интегрирование.
- Формула трапеций.
- Формула парабол.
- Формулы прямоугольников.
- Использование многочленов высших степеней.
- Квадратурная формула Гаусса.
- Оценка погрешности численного интегрирования.
- Приближенное вычисление несобственных интегралов.
Интегральное исчисление функции многих переменных
- Кратные (двойные, тройные и др.) интегралы.
- Задачи, приводящие к понятию кратного интеграла.
- Условия существования кратного интеграла.
- Классы интегрируемых функций.
- Свойства кратного интеграла.
- Теоремы о среднем значении для кратного интеграла.
- Вычисление кратных интегралов.
- Криволинейные координаты.
- Замена переменных в кратном интеграле.
- Цилиндрические и сферические координаты.
- Несобственные кратные интегралы.
- Приложения кратных интегралов.
- Численное интегрирование.
- Использование одномерных квадратурных формул.
- Кубатурные формулы.
- Многомерные кубатурные формулы.
- Метод статистических испытаний.
- Вычисление кратных интегралов методом Монте-Карло.
- Криволинейные интегралы, их свойства, условия существования и вычисление.
- Механические приложения криволинейного интеграла первого рода.
- Формула Грина.
- Условия независимости криволинейного интеграла от пути интегрирования.
- Вычисление криволинейного интеграла от полного дифференциала.
- Криволинейный интеграл в многосвязной области.
- Односторонние и двусторонние поверхности в пространстве.
- Площадь поверхности.
- Поверхностные интегралы и их приложения.
- Формула Стокса.
- Условия независимости криволинейного интеграла второго рода от пути интегрирования в пространстве.
- Формула Остроградского - Гаусса.
- Элементы теории поля.
- Скалярные и векторные поля.
- Векторные линии.
- Поток векторного поля и дивергенция.
- Циркуляция векторного поля и ротор.
- Простейшие типы векторных полей.
- Оператор Гамильтона.
- Правила действий с оператором Гамильтона.
-
Дифференциальные уравнения
- Геометрическая интерпретация решения ОДУ.
- Поле направлений.
- Задачи, приводящие к решению дифференциальных уравнений.
- Постановка задачи Коши.
- Интегpальное неpавенство.
- Теоpема существования и единственности pешения (теоpема Коши).
- Оценка pазности pешений двух уpавнений.
- Непpеpывная зависимость pешения от начальных условий и паpаметpа.
- Изоклины и их использование для пpиближенного постpоения интегpальных кpивых.
- Дифференциальные уравнения первого порядка.
- Диффеpенциальные уpавнения с pазделяющимися пеpеменными
- Одноpодные и квазиодноpодные уpавнения.
- Уpавнения в полных диффеpенциалах.
- Интегpиpующий множитель.
- Линейные диффеpенциальные уpавнения пеpвого поpядка.
- Уpавнения Беpнулли и Риккати.
- Особые точки и особые решения ОДУ первого порядка.
- Уpавнения, не pазpешенные относительно пpоизводной.
- Особенности составления дифференциальных уравнений в прикладных задачах.
- Ортогональные и изогональные траектории.
- Системы обыкновенных дифференциальных уравнений.
- Задача и теоpема Коши.
- Частное и общее pешения системы диффеpенциальных уpавнений.
- Оценка pазности двух pешений.
- Теоpема Коши о существовании и единственности pешения уpавнения высшего поpядка.
- Случаи понижения поpядка.
- Системы линейных дифференциальных уравнений.
- Опpеделитель Вpонского.
- Фундаментальная система pешений.
- Фоpмула Остpогpадского - Лиувилля.
- Теоремы о стpуктуpе общего pешения одноpодной и неодноpодной систем.
- Метод ваpиации постоянных.
- Формула Коши.
- Система линейных диффеpенциальных уpавнений с постоянными коэффициентами.
- Хаpактеpистическое уpавнение системы.
- Нахождение фундаментальной системы pешений в случае pазличных коpней хаpактеpистического уpавнения.
- Стpуктуpа фундаментальной системы pешений в случае кpатных коpней.
- Линейные дифференциальные уравнения высших порядков.
- Сведение к линейной системе.
- Опpеделитель Вpонского и стpуктуpа общего pешения одноpодного уpавнения.
- Общее pешение неодноpодного уpавнения.
- Метод Лагpанжа ваpиации постоянных.
- Понижение поpядка линейного диффеpенциального уpавнения.
- Линейные дифференциальные уpавнения с постоянными коэффициентами.
- Случай pазличных коpней хаpактеpистического уpавнения.
- Фоpмула сдвига.
- Случай кpатных коpней характеристического уравнения.
- Уpавнения Эйлеpа, Лагpанжа, Чебышева.
- Стpуктуpа частного pешения уpавнения с постоянными коэффициентами и специальной пpавой частью.
- Первые интегралы.
- Теоpема о локальном существовании системы пеpвых интегpалов.
- Понижение поpядка системы диффеpенциальных уpавнений при помощи пеpвых интегpалов.
- Симметричная форма записи нормальной автономной системы дифференциальных уравнений.
- Элементы теории устойчивости.
- Устойчивость системы линейных диффеpенциальных уpавнений.
- Теоpемы Ляпунова об устойчивости по пеpвому пpиближению.
- Функции Ляпунова.
- Теоpемы Ляпунова об устойчивости и асимптотической устойчивости.
- Теоpемы Четаева и Ляпунова о неустойчивости.
- Особые точки на фазовой плоскости.
- Фазовый поpтpет системы.
- Математическая модель сосуществования двух популяций.
- Краевые задачи для дифференциального уравнения.
- Линейная кpаевая задача, сведение ее к задаче Коши.
- Пpимеpы pешения кpаевой задачи.
- Приближенные методы решения дифференциальных уравнений.
- Интегpиpование диффеpенциальных уpавнений при помощи степенных pядов.
- Метод последовательных пpиближений.
- Метод ломаных Эйлеpа.
- Метод Рунге - Кутты.
- Дифференциальные уравнения первого порядка с частными производными.
- Линейное дифференциальное уpавнение.
- Уpавнения хаpактеpистик.
- Задача Коши.
- Квазилинейное дифференциальное уpавнение.
- Задачи математической физики.
- Классификация дифференциаотных уравнений в частных производных второго
- порядка.
- Основные уравнения математической физики.
- Метод Фурье.
- Основы метода конечных разностей.
- Понятие о сеточных методах.
- Аппроксимация производных конечными разностями.
- Простейшие разностные схемы.
- Основные понятия метода конечных элементов и метода граничных элементов.
- Типы конечных элементов.
- Граничные интегральные уравнения.
- Способы аппроксимации функций на границе.
-
Ряды и элементы функционального анализа
- Числовые ряды.
- Необходимый признак сходимости рядов.
- Свойства сходящихся рядов.
- Признаки сравнения знакоположительных рядов.
- Интегральный признак сходимости Коши и признак Даламбера.
- Радикальный признак Коши.
- Абсолютная и условная сходимости.
- Знакочередующиеся ряды, признак Лейбница.
- Умножение рядов.
- Функциональные ряды.
- Сходимость функциональных последовательностей и рядов.
- Равномерная сходимость функциональных последовательностей и рядов.
- Свойства равномерно сходящихся рядов.
- Комплексные степенные ряды.
- Действительные степенные ряды.
- Ряд Тейлора.
- Разложение элементарных функций в ряд Тейлора.
- Применение рядов в приближенных вычислениях.
- Ряды Фурье.
- Ортонормированные системы и ряды Фурье.
- Комплексная форма записи тригонометрического ряда Фурье.
- Ряды Фурье по тригонометрической системе.
- Порядок малости коэффициентов Фурье.
- Дифференцирование и интегрирование тригонометрических рядов Фурье.
- Разложение функций в тригонометрические ряды Фурье на отрезке [-π,π].
- Сдвиг отрезка разложения.
- Разложение функций в тригонометрические ряды Фурье на отрезке [-l,l].
- Разложение четных и нечетных функций.
- Разложение функций в ряды Фурье по синусам и по косинусам.
- Дискретное преобразование Фурье.
- Быстрое преобразование Фурье.
- Интеграл Фурье.
- Представление функций интегралом Фурье.
- Интеграл Фурье в случае четных и нечетных функций.
- Комплексная форма интеграла Фурье.
- Преобразование Фурье.
- Косинус-преобразование и синус-преобразование Фурье.
- Свойства преобразования Фурье.
- Ряды в нормированных пространствах.
- Нормированные пространства.
- Банаховы пространства.
- Подпространства нормированных пространств.
- Сепарабельные пространства.
- Сходимость рядов в банаховых пространствах.
- Банаховы пространства со счетным базисом.
- Счетные базисы в пространстве непрерывных функций.
- Ортонормированные системы в гильбертовых пространствах.
- Гильбертовы пространства.
- Расстояние до подпространства.
- Ортогональность.
- Ортонормированные системы и ряды Фурье.
- Ортонормированные базисы.
- Ортогонализация и существование ортогонального базиса.
- Мера Лебега.
- Измеримые функции.
- Интеграл Лебега.
- Банахово пространство L1 [a,b].
- Гильбертово пространство L2 [a,b].
- Тригонометрическая система.
-
Функции комплексного переменного
- Комплексная плоскость.
- Алгебраическая и тригонометрическая формы записи комплексного числа.
- Бесконечно удаленная точка. Сфера Римана.
- Последовательности и ряды комплексных чисел.
- Степенные ряды, круг сходимости.
- Двусторонний степенной ряд.
- Функции комплексного переменного.
- Предел и непрерывность функций комплексного переменного.
- Элементарные функции комплексного переменного.
- Логарифмическая функция.
- Обратные тригонометрические функции.
- Дифференцирование функций комплексного переменного.
- Производная функции комплексного переменного.
- Необходимые и достаточные условия дифференцируемости.
- Правила дифференцирования функций комплексного переменного.
- Аналитические функции.
- Геометрический смысл аргумента и модуля производной.
- Теорема о единственности аналитической функции.
- Восстановление аналитической функции по ее действительной или мнимой части.
- Понятие об аналитическом продолжении.
- Интегрирование функций комплексного переменного.
- Интегральные теоремы Коши.
- Независимость интеграла от пути интегрирования.
- Формула Ньютона - Лейбница.
- Интегральная формула Коши.
- Высшие производные аналитической функции.
- Достаточные условия аналитичности функции.
- Комплексный потенциал плоского векторного поля.
- Функциональные ряды на комплексной плоскости.
- Равномерная сходимость функциональных рядов.
- Свойства равномерно сходящихся рядов.
- Разложение функций в ряд Тейлора.
- Ряд Лорана.
- Нахождение всевозможных разложений функции по заданным степеням.
- Связь ряда Лорана с рядом Фурье.
- Нули и особые точки аналитической функции.
- Нули аналитической функции.
- Изолированные особые точки.
- Бесконечно удаленная точка как особая.
- Классификация аналитических функций по их особым точкам.
- Физическое толкование полюсов аналитической функции.
- Вычеты в изолированных особых точках.
- Применение вычетов для вычисления интегралов.
- Логарифмический вычет.
- Геометрические принципы теории функций комплексного переменного.
- Конформные отображения и их свойства.
- Теорема Римана.
- Принцип соответствия границ.
- Принцип максимума модуля функции.
- Принцип симметрии.
- Линейное отображение.
- Дробно линейное отображение.
- Целая степенная функция.
- Показательная функция.
- Функция Жуковского.
- Тригонометрические и гиперболические функции.
- Однозначные ветви многозначных обратных функций.
-
Вариационное исчисление и оптимальное управление
- Задачи, приводящие к вариационным проблемам.
- Основные леммы вариационного исчисления.
- Вариационные задачи с фиксированными границами.
- Простейшая задача вариационного исчисления.
- Функционалы от нескольких функций.
- Функционалы с производными высшего порядка.
- Функционалы от функций многих переменных.
- Канонический вид уравнений Эйлера.
- Вариационные задачи с подвижными границами.
- Задача с подвижными концами.
- Задача с подвижными границами.
- Экстремали с угловыми точками.
- Задачи на условный экстремум.
- Основные типы задач на условный экстремум.
- Необходимые условия в задаче Лагранжа.
- Необходимые условия в изопериметрической задаче.
- Некоторые примеры.
- Принцип взаимности в изопериметрических задачах.
- Задача Больца и задача Майера.
- Достаточные условия экстремума.
- Слабый экстремум.
- Условие Якоби.
- Инвариантный интеграл Гильберта.
- Сильный экстремум.
- Постановка задачи оптимального управления.
- Задача Лагранжа в форме Понтрягина.
- Некоторые задачи с ограничениями в классическом вариационном исчислении.
- Линейные задачи оптимального управления.
- Принцип максимума.
- Задача быстродействия.
- Линейная задача оптимального быстродействия.
- Задача синтеза управления.
- Задача с подвижными концами.
- Неавтономные системы.
- Понятие особого управления.
- Метод динамического программирования.
- Принцип оптимальности.
- Уравнение Беллмана.
- Уравнение Беллмана в задаче быстродействия.
- Связь метода динамического программирования с принципом максимума.
- Прямые методы вариационного исчисления.
- Формулировка вариационных задач.
- Операторное уравнение.
- Вариационное уравнение.
- Примеры построения функционала по вариационному уравнению.
- Исследование выпуклости функционала.
- Методы решения вариационных задач.
- Минимизирующие последовательности.
- Методы приближенного решения вариационных задач.
- Собственные значения симметрического оператора.
- Приближенное решение задачи на собственные значения.
- Двойственные вариационные задачи.
- Альтернативные функционалы.
- Построение альтернативного функционала.
- Оценка погрешности приближенного решения.
- Приложения вариационных методов.
- Колебания струны.
- Колебания мембраны.
- Аэродинамическая задача Ньютона.
- Вопросы устойчивости конструкций.
-
Теория вероятностей, математическая статистика и случайные процессы
- Случайные события.
- Пространство элементарных исходов.
- События, действия над ними.
- Сигма-алгебра событий.
- Классическое определение вероятности.
- Вычисление вероятностей с помощью формул комбинаторики.
- Геометрическое определение вероятности.
- Статистическое определение вероятности.
- Аксиоматическое определение вероятности.
- Условная вероятность.
- Схема Бернулли.
- Формула умножения вероятностей.
- Независимые и зависимые события.
- Формула полной вероятности.
- Формула Байеса.
- Схема Бернулли.
Одномерные случайные величины.
- Функция распределения случайной величины.
- Дискретные и непрерывные случайные величины.
Многомерные случайные величины.
- Многомерная случайная величина.
- Совместная функция распределения.
- Дискретные двумерные случайные величины.
- Независимые случайные величины.
- Многомерное нормальное распределение.
Функции от случайных величин.
- Примеры функциональной зависимости между случайными величинами.
- Функции от одномерной случайной величины.
- Скалярные функции от случайного векторного аргумента.
- Формула свертки.
- Векторные функции от случайного векторного аргумента.
- Линейные преобразования нормально распределенных случайных величин.
- Метод линеаризации.
Числовые характеристики случайных величин.
- Математическое ожидание случайной величины.
- Математическое ожидание функции от случайной величины.
- Свойства математического ожидания.
- Дисперсия.
- Моменты высших порядков.
- Ковариация и коэффициент корреляции случайных величин.
Условные характеристики случайных величин.
- Условные распределения.
- Условные числовые характеристики.
Предельные теоремы теории вероятностей.
- Сходимость последовательности случайных величин.
- Неравенства Чебышева.
- Закон больших чисел.
- Характеристическая функция.
- Центральная предельная теорема.
Генеральная совокупность.
- Выборка.
- Выборочные характеристики.
- Основные задачи математической статистики.
- Предварительная обработка результатов эксперимента.
Точечные оценки.
- Состоятельные, несмещенные и эффективные оценки.
- Понятие достаточных статистик.
- Методы получения точечных оценок.
Интервальные оценки и доверительные интервалы.
- Построение интервальных оценок.
- Метод доверительных множеств.
Проверка гипотез о параметрических моделях.
- Проверка двух простых гипотез.
- Критерий Неймана --- Пирсона.
- Определение объема выборки.
- Сложные параметрические гипотезы.
- Последовательный критерий отношения правдоподобия
Проверка непараметрических гипотез.
- Критерии согласия.
- Простая и сложная гипотезы.
- Критерии независимости.
Основы корреляционного анализа.
- Исходные понятия.
- Анализ парных связей.
Основы регрессионного анализа.
- Метод наименьших квадратов.
- Статистический анализ регрессионной модели.
- Выбор допустимой модели регрессии.
Основы дисперсионного анализа.
- Однофакторный дисперсионный анализ.
- Двухфакторный дисперсионный анализ.
Случайная функция, случайный процесс и случайная последовательность.
- Математическое ожидание и ковариационная функция случайного процесса.
- Стационарные случайные процессы.
- Нормальные процессы.
- Процессы с независимыми приращениями.
- Винеровский процесс.
- Марковские процессы.
- Пуассоновский процесс.
Элементы стохастического анализа.
- Сходимость в смысле среднего квадратичного (СК-сходимость).
- Непрерывность случайного процесса.
- Дифференцируемость случайного процесса.
- Интегрируемость случайного процесса..
- Действие линейного оператора на случайный процесс.
- Эргодические случайные процессы.
Спектральная теория стационарных случайных процессов.
- Стационарные случайные процессы с дискретным спектром.
- Стационарные случайные процессы с непрерывным спектром.
- Белый шум.
- Преобразование стационарного случайного процесса при его прохождении через линейную динамическую систему.
Марковские процессы с дискретными состояниями и цепи Маркова.
- Уравнения Колмогорова для вероятностей состояний.
- Процесс гибели --- размножения и циклический процесс.
Элементы теории массового обслуживания.
- Простейший поток.
- Время ожидания и время обслуживания.
- Основные принципы построения марковских моделей массового обслуживания.
- Системы массового обслуживания с ожиданием.
- Стационарные режимы функционирования системы обслуживания.
Стохастические модели состояния.
- Случайные возмущения в динамической системе.
- Линейные стохастические дифференциальные уравнения.
- Стохастические интегралы и дифференциалы.
-
Методы конечномерной оптимизации и исследование операций
- Постановки задач оптимизации и их классификация.
- Основные численные методы одномерной и многомерной оптимизации, условия их сходимости.
- Порядок метода.
- Основные численные методы условной оптимизации.
- Основы линейного программирования.
- Задачи, приводящие к задачам линейного программирования.
- Формы записи задач линейного программирования.
- Двойственная задача линейного программирования.
- Симплекс-метод.
- Основные утверждения линейного программирования.
- Симплекс-метод при известном допустимом базисном решении.
- Нахождение допустимого базисного решения.
- Анализ на чувствительность.
- Целочисленное программирование.
- Методы решения задач целочисленного программирования.
- Метод отсекающих плоскостей (метод Гомори).
- Метод ветвей и границ.
- Задачи транспортного типа.
- Классическая транспортная задача.
- Транспортная задача с промежуточными пунктами.
- Задача о назначениях.
- Венгерский метод решения задачи о назначениях.
- Задача выбора кратчайшего пути.
- Симплексный метод решения задач транспортного типа.
- Марковские модели принятия решений.
- Принятие решений при конечном и бесконечном горизонтах планирования.
- Марковская задача принятия решений и метод линейного программирования.
- Задачи принятия решений в условиях риска и неопределенности.
- Одноэтапные процедуры принятия решений в условиях риска.
- Использование экспериментальных данных при принятии решений в условиях риска.
- Многоэтапные процедуры принятия решений в условиях риска.
- Одноэтапные процедуры принятия решений в условиях неопределенности.
- Элементы теории игр.
- Игры двух участников с нулевой суммой.
- Решение игр двух участников с нулевой суммой в смешанных стратегиях.
- Игры двух участников с ненулевой суммой.
- Основные понятия и этапы имитационного моделирования.
- Моделирование случайных величин и случайных событий.
- Имитационное моделирование как вычислительный эксперимент.
- Построение и эксплуатация имитационных моделей.
-
Алгебра и геометрия
- Details
- Category: Научная работа
На кафедре ФН-12 параллельно развиваются несколько научных направлений.
Крищенко А.П., д.ф-м.н., чл.корр. РАН, профессор, зав.каф.
Основное направление исследований: Основные направления научной деятельности связаны с анализом, управлением и математическим моделированием нелинейных систем. Разработаны дифференциально-геометрические методы анализа нелинейных систем и синтеза алгоритмов управления. Создан метод локализации периодических решений, инвариантных компактов и областей с хаотической динамикой нелинейных непрерывных и дискретных систем.
Потенциальные темы для курсовых работ студентов:
-
Иследование и математическое моделирование нелинейных систем дифференциальных уравнений,
описывающих динамику процессов в медицине, биологии, экологии. - Построение алгоритмов управления системами техниеских объектов.
- Реконструкция изображений по неполной информации.
Ссылки на публикации:
- https://scholar.google.ru/citations?hl=ru&user=DjJs_0kAAAAJ&view_op=list_works&sortby=pubdate
- https://www.scopus.com/authid/detail.uri?authorId=7004235055
Головина А.М., к.ф.-м.н.
Основное направление исследований: Объектом исследования являются эллиптические дифференциальные операторы с разбегающимися возмущениями во всём пространстве, различного рода областях и волноводах. Под разбегающимися возмущениями понимаются функции или операторы, локализованные в областях, расположенных на большом расстоянии друг от друга. Были проанализированы поведение резольвенты, общего, непрерывного и точечного спектров рассматриваемых операторов. Построены полные асимптотические разложения резольвенты и собственных значений рассматриваемого оператора при различных случаях кратности предельного собственного значения. Изучались вопросы сходимости общего, непрерывного и дискретного спектров.
Ссылки на публикации:
Горяинов В.Б., д.ф.-м.н., профессор
Основное направление исследований: применение робастных статистических методов для идентификации нелинейных случайных процессов с дискретным временем (временных рядов) и для анализа многомерных статистических данных (метод главных компонент, факторный анализ). Примерами нелинейных временных рядов являются авторегрессионные процессы со случайными коэффициентами, процессы пороговой авторегрессии, процессы экспоненциальной авторегрессии. Классические статистические методы анализа данных, такие как выборочное среднее или метод наименьших квадратов, являются наилучшими в предположении, что ошибки наблюдений имеют нормальное (гауссовское) распределение. Однако эти методы резко теряют свою эффективность при нарушении предположения о нормальности. Робастные методы, лишь немного уступая классическим в нормальной модели, значительно их превосходят в случае даже небольших отклонениях вероятностного распределения ошибок от нормального.
Потенциальные темы для курсовых работ студентов:
- Оценки наименьших модулей параметров билинейной авторегрессии.
- Робастные методы анализа главных компонент.
Ссылки на публикации:
- https://www.scopus.com/authid/detail.uri?authorId=35974804800
- https://www.elibrary.ru/author_profile.asp?authorid=78798
Юрченков А.В., к.ф.-м.н.
Основное направление исследований: подавление влияний внешних возмущений в задачах оценивания, фильтрации и управления техническими системами. В качестве объектов рассмотрения выбираются динамические системы, на которые действует стохастическое возмущение с неточно заданными параметрами. Для описания характеристик внешнего возмущения используется относительная энтропия, где в качестве эталонного возмущения рассматриваетс класс последовательностей случайных векторов с нормальным распределением. В качестве целевой функции выбирается анизотропийная норма соответствующей системы.
Потенциальные темы для курсовых работ студентов:
- Построение стабилизирующего управления для квадрокоптера на основе линейной модели.
- Синтез регулятора для управления динамической системы с неточно заданными параметрами.
Ссылки на публикации:

