- Details
- Category: Учебно-методическая работа
Изучение кинематики начинается с разделов, посвященных кинематике точки и кинематике простейших движений твердого тела. Это определяет особую важность методической проработки этих вопросов для более глубокого усвоения их обучающимися. Методические пособия, посвященные этим вопросам, издавались в помощь студентам, выполняющим домашние задания по указанным темам. Общим во всех методических пособиях являлся акцент на векторном представлении кинематических характеристик движения (с нанесением на чертеже траектории, скорости и ускорения точки, их составляющих, угловых скоростей и угловых ускорений тел). Результаты расчетов доводятся до числа.
Методические указания [1] содержат варианты курсового задания и разбор примеров решения типовых задач. В условиях задач по кинематике точки использовался лишь координатный способ задания движения (в декартовой системе координат). В работе [2] задания были дополнены вариантами с исходным заданием движения точки в полярной системе координат и естественным способом. При этом в каждом варианте необходимо было получить все составляющие скорости и ускорения точки, исходя из разных способов задания ее движения и разных используемых координатных осей.
В работе [3] дано краткое изложение основных теоретических вопросов, относящихся к рассматриваемым темам, так что пособие могло использоваться при самостоятельной проработке тем студентами, обучающимися по вечерней форме. Приведены вопросы для самопроверки знаний.
В связи с изменением учебных планов и введением единой курсовой расчетно-графической работы были созданы задания по указанным темам, в которых исследовалось движение не абстрактных материальных точек, а точек, принадлежащих телам, совершающим простейшие движения в рассматриваемых механизмах [4]. Схемы этих механизмов и результаты расчетов использовались в качестве исходных данных для решения других разделов курсовой работы: по плоскому движению твердого тела, сложному движению точки и задач статики (схемы механизмов). В помощь к выполнению данного задания была написана работа [5], содержащая краткое теоретическое изложение материала, примеры решения задач и варианты для самоконтроля знаний. Методически более подробно рассмотрены вопросы, относящиеся к переходу от одного способа задания движения точки к другому, показано различие в определении проекции ускорения на касательную ось, исходя из естественного способа задания движения точки, и проекции на ось, совпадающую со скоростью, исключено использование понятий «алгебраическая угловая скорость» и «алгебраическое угловой ускорение».
В настоящее время подготовлено задание, представленное в [6]. По сравнению с предыдущим обновлены схемы механизмов, приведены примеры решения задач с использованием ЭВМ. В помощь к выполнению этого задания подготовлена работа [7].
Литература
- Бочаров В.К., Бурмистров Б.А., Иванова К.М., Козлов И.С., Кутлер В.П. Кинематика точки. Простейшие движения твердого тела. Кинематика сложного движения точки. / Учебное пособие. – М. МВТУ им. Н.Э. Баумана, 1973. – 54 с.
- Горина Т.И., Кинелев В.Г. Кинематика точки. Простейшие движения твердого тела / Методические указания. – М.: МВТУ им. Н.Э. Баумана, 1979. – 30 с.
- Обучающая программа по разделу «Кинематика». Часть 1. / Методические указания для студентов вечернего факультета по разделу «Кинематика» Курса теоретической механики. – М.: МВТУ им. Н.Э. Баумана, 1985. – 36 с.
- Брусенцова Е.А., Пилюгина Н.Н., Пожалостин А.А. Кинематика точки. Простейшие движения твердого тела / Методические указания и варианты курсовой работы № 1. – М.: Изд-во МГТУ им. Н.Э. Баумана, 1986. – 54 с.
- Болотникова Я.А., Панкратов А.А., Пожалостин А.А., Шкапов П.М. Кинематика точки. Простейшие движения твердого тела / Методические указания к курсовой расчетно-графической работе №1. – М.: Изд-во МГТУ им. Н.Э. Баумана, 1991. – 52 с.
- Виноградов А.А., Пилюгина Н.Н., Феоктистова О.П. Кинематика точки. Простейшие движения твердого тела / Методические указания и варианты домашнего задания. – М.: Изд-во МГТУ им. Н.Э. Баумана, 1994. – 54 с.
- Лапшин В.В. Кинематика точки. Простейшие движения твердого тела / Методические указания к выполнению домашнего задания. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2003.
- Details
- Category: Учебно-методическая работа
Курсовое задание по данной теме было предложено студентам в цикле заданий по основным темам курса «Теоретическая механика» [1]. Это задание создавалось под руководством И. М. Брызгалова.
Для каждого студента выдавалось персональное задание, в котором рассматривалась механическая система (механизм), имеющая две степени свободы.
Необходимо было определить в данном положении механизма скорости и ускорения точек звеньев и угловые скорости и ускорения звеньев механизма. Решение производилось аналитическим методом с иллюстрацией этого метода построением многоугольников скоростей и ускорений точек звеньев механизма.
Достоинством этого задания был тот факт, что в нем многовариантность создавалась многообразием схем механических систем, оригинальным заданием законов движения точек тел звеньев механизмов.
Студент при выполнении задания углублялся в суть решения, анализ метода решения задачи. Одновременно появилась необходимость совершенствовать систему курсовых заданий для студентов приборостроительных специальностей и для студентов вечернего факультета. Были подготовлены задания [2, 3], в которых также выдавались студентам персональные варианты задания.
Схемы механических систем (механизмов) не повторялись, системы имели одну степень.
В заданиях подробно разбирались решения типовых вариантов задания.
Далее было произведено некоторое упорядочение схем курсовых заданий и типов задач в курсовых заданиях [4, 5].
Для студентов вечернего факультета было предложено пособие доц., к.т.н. В. П. Трониной – заведующей секцией вечернего факультета на кафедре ТМ [6]. В этом пособии подробно изложены темы «Кинематика точки», «Простейшие движения твердого тела», «Плоское движение твердого тела». К каждой теме подобраны примеры, приведены решения задач, вопросы для самопроверки знаний и задачи для самостоятельного решения.
В работе [7] предложена курсовая работа для студентов-вечерников, состоящая из двух задач. В первой задаче исследуется плоское движение механизмов с одной степенью свободы, в второй – сложное движение точки.
В середине восьмидесятых годов прошлого века в связи с переходом (временным) на преподавание теоретической механики в два семестра были введены курсовые работы [8].
Варианты заданий курсовой работы имели тесную тематическую связь. Механическая система строилась как некоторая «машина», которая имеет привод, передаточный и исполнительный механизмы. Однако, в заданиях по темам студент имел схемы отдельных частей этой «машины». Необходимо только перенести исходные данные с предыдущего задания на последующее.
В теме «Простейшие движения твердого тела» рассматриваются механизмы типа редукторов, исполнительный механизм состоит из тел, совершающих плоское движение, переход от одного звена к другому или к другому механизму осуществляется с помощью соединений, в которых заложены задачи сложного движения точки.
В учебный процесс в 70-80-х годах прошлого столетия внедрялось использование ЭВМ в учебный процесс [9].
Кроме того, с введением нового цикла заданий в учебный процесс, более качественных и более емких, потребовалась учебная литература нового назначения. Эта литература должна была помочь студентам выполнить курсовое задание, разобраться в том, какие типовые схемы механических систем и задач встречаются в данной теме курса, освоить методы решения данного класса задач.
Идея создания пособий такого типа была решена кафедрой ТМ МВТУ еще в
В пособии [10] даны также типовые простейшие примеры для самостоятельного решения студентом.
Литература
- Курсовое задание по теоретической механике «Плоское движение твердого тела», каф. ТМ. И. М. Брызгалов, Я. А. Качмарчик, В. П. Печников, П. Г. Русанов. Изд. МВТУ, М. 1970.
- Горина Т. И., Русанов П. Г. Кинематика плоского движения твердого тела. Задание по курсу «Теоретическая механика». Изд. МВТУ, М. 1974.
- Тронина В. П., Виляевская Н. И., Ефремов Г. Ф. Задание для студентов вечернего отделения по курсу «Теоретическая механика», раздел «Кинематика». Изд. МВТУ, М. 1974.
- Русанов П. Г., Северова Л. В., Болотникова Я. А. Методические указания к курсовой работе по разделу «Кинематика плоского движения твердого тела». Изд. МВТУ, М. 1979.
- Горина Т. И., Назаренко Б. П., Русанов П. Г. Методические указания по выполнению курсовой работы по разделу «Кинематика плоского движения твердого тела». Изд. МВТУ, М. 1982.
- Тронина В. П., Дронг В. И. Обучающая программа по разделу «Кинематика», ч. 1. Методические указания для студентов вечернего факультета по разделу «Кинематика» курса теоретической механики. Изд. МВТУ, М. 1985.
- В. П. Тронина, Т. М. Тушева, Ю. Д. Плешаков. Курсовая работа по кинематике для вечернего факультета и методические указания по её выполнению. Изд. МВТУ. М. 1983.
- Кинематика плоского движения твердого тела. Методические указания к курсовой работе по теоретической механике. Б. П. Назаренко, Л. В. Северова, Е. Н. Солохин, Ю. М. Степанчук. Изд. МГТУ, М. 1987.
- Решение задач по курсу «Теоретическая механика с использованием ЭВМ». В. В. Дубинин, Г. М. Максимов, Б. П. Назаренко, П. Г. Русанов, Е .Н. Солохин, Ю. М. Степанчук. Изд. МГТУ, М. 1988.
- Кинематика плоского движения твердого тела. В. В. Дубинин, Б. П. Назаренко, Л. В. Северова, Е. Н. Солохин, Ю. М. Степанчук. Изд. МГТУ, М. 1989.
- Details
- Category: Учебно-методическая работа
Многие студенты, проходящие обучение на кафедре, участвуют в научных конференциях и выставках научно-технического творчества молодёжи. Их работы отмечены медалями, стипендиями Президента РФ и Правительства РФ.

Начиная свою научную работу под руководством преподавателей кафедры, студенты МГТУ им. Н.Э. Баумана выступают с докладами на кафедральных, университетских, Всероссийских и Международных научных конференциях, участвуют в выставках, публикуются в рецензируемых изданиях разного уровня. Лучшие из них могут поступить в аспирантуру кафедры.
.


Развивается сотрудничество с музеем Н.Е. Жуковского в ЦАГИ.
С 2013 г. студенческие научные конференция проходят в форме расширенного выездного заседания кафедры в конференц-зале этого музея. В заседании и обсуждении научных докладов студентов и аспирантов участвуют профессора и преподаватели кафедры, а также научные сотрудники из институтов РАН. Директор музея В.Г. Каркашадзе радушно встречает гостей и знакомит собравшихся с экспозицией музея.

На научной конференции «Студенческая научная весна -2014» в музее ЦАГИ имени профессора Н.Е. Жуковского
Традиции, заложенные Н.Е. Жуковским, основателем кафедры теоретической механики, продолжают поддерживаться и развиваться. К педагогической, методической, научной и общественной деятельности подключаются всё новые молодые преподаватели, аспиранты и студенты, что является залогом дальнейшего успешного развития кафедры в современных условиях.
- Details
- Category: Учебно-методическая работа
На кафедре существует богатая коллекция моделей механизмов и устройств для демонстрации законов механики, которая начала формироваться еще при Н.Е. Жуковском. Коллекция кабинета приборов постоянно обновляется, пополняясь приборами нового поколения и дизайна.
Кабинет приборов
http://fn.bmstu.ru/en/learning-works-fs-11/calendar-plans-fs11/32-nuk-fn/fn-dep/ter-meh/study-methodological-work#sigProId806e1becc3
По инициативе К.С. Колесникова на кафедре в 70‑х годах ХХ века была создана лаборатория теории колебаний с научно-учебными установками для исследования колебаний систем с сосредоточенными и распределенными параметрами. Результаты экспериментов, полученных на некоторых установках, использовались в диссертационных работах аспирантов и сотрудников кафедры.
Установки для демонстрации флаттера и динамического гашения колебаний
Аспиранты К.С. Колесникова, будущие доценты – М.М. Ильин, В.С. Курдин и Е.Н. Солохин
у созданных ими экспериментальных установок (1970-е годы)
Лаборатория
С 90-х годов ХХ века под руководством и при участии В.В. Дубинина стали разрабатываться и внедряться в учебный процесс автоматизированные лабораторные работы. Установки позволяют проводить эксперименты и обрабатывать их результаты на компьютере. В этом направлении активно работали В.В. Дубинин, В.В. Витушкин, Г.И. Дубровина, Б.П. Назаренко, а также доцент кафедры ИУ1 Ю.Н. Жигулёвцев.
http://fn.bmstu.ru/en/learning-works-fs-11/calendar-plans-fs11/32-nuk-fn/fn-dep/ter-meh/study-methodological-work#sigProId7f8c462d83
Автоматизированные лабораторные установки
- Details
- Category: Учебно-методическая работа
В задачах курсовых заданий на сложное движение точки применяются теоремы о сложении скоростей и ускорений, и студенты обучаются методам вычисления скоростей и ускорений точек с помощью этих теорем.
Условно задачи на сложное движение точки можно представить как задачи двух видов – «прямые» и «обратные». В прямых задачах по известному закону относительного движения точки и параметрам переносного движения требуется найти абсолютные скорость и ускорение точки. Эти задачи студенты, как правило, быстро воспринимают и умеют хорошо решать. К «обратным» можно отнести те задачи, в которых известна абсолютная траектория точки. Требуется найти кинематические характеристики, оставшиеся неизвестными в абсолютном, относительном или переносном движениях. Такие задачи вызывают у студентов много вопросов и решаются хуже, чем «прямые». Поэтому в заданиях для студентов долго преобладали «прямые» задачи.
Методика решения «прямых» задач с переносными вращательным и поступательным движениями изложена в учебном пособии «Решение задач по кинематике» Л. Г. Тихоновой и Т. И. Гориной (Изд. МВТУ, 1967)
В 1973 г. опубликовано учебное пособие по кинематике, содержащее варианты «прямых» и «обратных» задач сложного движения точки (Кинематика точки. Кинематика простейших движений твердого тела. Кинематика сложного движения точки. Авторы: В. К. Бочаров, Б. А. Бурмистров, К. И. Иванова, И. С. Козлов, В. П. Кутлер).
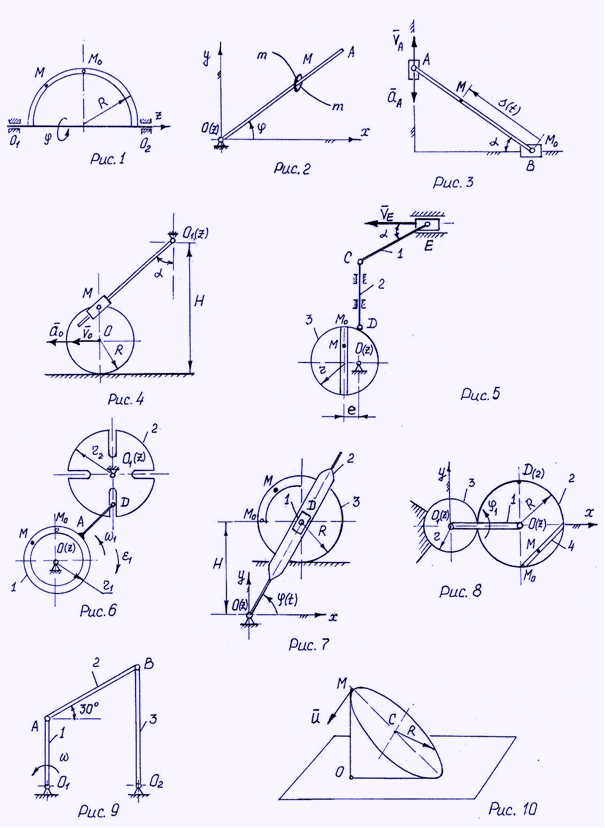
В «прямых» задачах использованы как традиционные в то время схемы с переносным вращательным движением (рис. 1) (см. «Сборник заданий для курсовых работ по теоретической механике под ред. А. А. Яблонского. – М.: Высшая школа, 1972), так и задачи с переносным плоским движением – их еще только две. В «обратных» задачах представлено несколько схем кулисных механизмов, обращенного эллиптического циркуля, а также задачи, которые показаны на рис. 2.
Кольцо М (материальная точка), надетое на стержень ОА, движется по траектории m – m в плоскости хОу, вращая стержень вокруг оси O(z). Заданы уравнения движения точки M x=x(t), y=y(t), задано ее начальное положение (при t=0). Требуется определить при t=t1 угловые скорость и ускорение стержня ОА, а также относительные (по отношению к стержню) скорость и ускорение точки М. Методика решения такого вида задач (рис. 2), а также решение «прямых» задач содержатся в методических указаниях по выполнению этого задания (Е. С. Веселый, П. В. Занозин, Л. Е. Ефремова, Б. А. Бурмистров «Статика – кинематика», изд. МВТУ, 1974). В это же время изданы и методические указания для студентов вечернего факультета, содержащие исключительно «прямые» задачи с переносным вращательным движением с подробными пояснениями и примерами решения (1974 г. под ред. В. П Трониной, авторы – В. П. Тронина, Н. И. Виляевская, Г. Ф Ефремов; и в 1982 г. – с большим количеством новых вариантов – В. П. Тронина, Ю. Д. Плешаков, Г. М. Тушева).
В 1980 г. для студентов дневных факультетов издано методическое пособие, содержащее 36 вариантов курсового задания, каждый из которых состоял из «прямой» и «обратной» задач (П. В. Занозин, Н. Н. Пилюгина, Г. М. Тушева «Кинематика сложного движения точки». МВТУ).
Здесь из 72-х задач 11 включали звенья с плоским движением как в «прямых» (рис. 3), так и в «обратных» задачах (рис. 4).
По заказу министерства высшего образования СССР через НПО «Союз-вузприбор» в 1983 г. была издана обучающая программа по теме «Кинематика сложного движения точки» объемом в 80 кадров (авторы: З. И. Тихонова и Г. М. Тушева). Программа предназначалась для студентов технических вузов страны и содержала методику и примеры решения «прямых» и «обратных» задач.
Обобщением накопленного опыта по методике решения задач явились «Методические указания к выполнению курсовой работы и решению задач по теме «Кинематика сложного движения точки», изданные в 1985 г. под ред. К.С. Колесникова (авторы: Дубинин В. В., Занозин П. В., Солохин Е. Н., Орфаницкая Л. П.), изд. МВТУ. Здесь проведена четкая классификация задач, рассмотрены все случаи относительного и переносного движений, даны необходимые пояснения и многочисленные примеры: 36 решений и 16 задач для самостоятельных практических занятий.
Качественно новый подход к структуре вариантов задания по сложному движению точки содержится в методических указаниях, изданных в1987 г. (Кинематика плоского движения твердого тела. Кинематика сложного движения точки под ред. К. С. Колесникова. Авторы: В. В. Дубинин, Г. Ф. Ефремов, А. И. Пастухов. Изд. МВТУ).
Схема каждого из 32-х вариантов теперь представляет собой комплекс из двух задач – из «прямой» для точки М и «обратной» для точки D. В большинстве вариантов сначала решается «обратная» задача – при известном абсолютном движении точки D механизма получить угловые скорость и ускорение звена, несущего на себе подвижную точку М (рис. 5). Затем рассматривается «прямая» задача, в которой определяются абсолютные скорость и ускорение точки М, относительное движение которой задано. Часть задач (рис. 6) решается в любом порядке.
Для промежуточного контроля знаний студентов в 1990 г. составлены и тиражированы 32 варианта «прямых» и «обратных» задач экзаменационной сложности (Материалы для КСР по теме «Кинематика сложного движения точки», авторы М. М. Ильин и Г. М. Тушева).
В 1997 г. были подготовлены к изданию в редакции МГТУ материалы методических указаний и новой редакции вариантов курсовой работы по теме «Сложное движение точки». Авторы: Дубинин В. В., Гатауллина Г. И., Тушева Г. М. и Ремизов А. В. Работа содержит теперь 44 варианта комплексных задач с использованием самых разнообразных плоских и пространственных механизмов. Это дает возможность преподавателю, ведущему практические занятия в группах, выбрать для каждого студента наиболее подходящий вариант.
Больше половины схем вариантов – новые задачи. По-прежнему, для точки D решается «обратная» задача, а затем для точки М – «прямая» (рис. 7). Введены задачи «обратного» типа, в которых назначается подвижная система отсчета и требуется найти относительные скорость и ускорение точки D(2) (звено 2) относительно звена 1, с которым связана подвижная система отсчета.
Так, в планетарном механизме (рис. 8) кривошип 1, вращаясь вокруг оси О1(z) неподвижной шестерни 3, приводит в движение шестеренку 2. Связав с кривошипом 1 подвижную систему отсчета хО1у , нужно найти для точки D(2) шестерни 2 относительные скорость и ускорение. Для точки М, которая движется вдоль паза 4 на шестерне 2, задано относительное движение, требуется найти абсолютные скорость и ускорение.
Предусмотрено выполнение каждого варианта задания с помощью ЭВМ – для разных положений механизма можно в диапазоне времени 0 ≤t ≤ 1 с получить характеристики относительного, переносного и абсолютного движений точек М и D.
В 2001 г. подготовлены к печати в редакции МГТУ «Методические указания по выполнению задания и решению задач по теме «Кинематика сложного движения точки» – авторы: Дубинин В. В., Гатауллина Г. И., Тушева Г. М.
В последние годы на кафедре проводится работа по составлению задачника для подготовки студентов к олимпиадам по теоретической механике. В разделе «Сложное движение точки» систематизированы и разобраны наиболее интересные задачи прошедших олимпиад. В задачнике представлены и короткие задачи, которые, как известно, очень эффективно используются в учебных и контрольных целях (Тушева Г. М.). На рис. 9 в механизме шарнирного четырехзвенника кривошип 1 вращается с угловой скоростью w1=w, O1A=AB=l. Связав подвижную систему отсчета с кривошипом 1, найти для заданного положения механизма кориолисово ускорение точки В звена 2.
На рис. 10 круговой конус с прямым углом при вершине и радиусом основания, равным R, катится без скольжения по горизонтальной плоскости так, что скорость центра его основания vc=v. По ободу основания конуса движется точка М со скоростью u. Найти величину кориолисова ускорения для заданного положения точки М.