4.2. Термодинамические потенциалы
Описание равновесных термодинамических процессов может быть выполнено с помощью метода термодинамических потенциалов, разработанного в 1873 - 78 годах американским физиком-теоретиком Джозайя Уиллардом Гиббсом (1839 - 1903). Этот метод аналогичен использованию в механике потенциальной энергии для описания консервативных механических систем.
Метод термодинамических потенциалов основывается на возможности введения для равновесных процессов функций состояния, полные дифференциалы которых описывают изменение состояния термодинамической системы.
Основное уравнение термодинамики равновесных процессов (4.4) 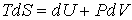 , , | (4.20) |
совместно с уравнением состояния
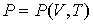 | (4.21) |
и выражением для внутренней энергии
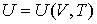 | (4.22) |
образуют систему из трех уравнений, связывающую между собой пять функций состояния: 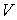 , 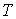 , 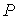 , 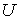 и 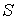 . Если в качестве независимых параметров выбрать объем 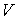 и температуру 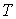 , то система уравнений (4.20) - (4.22) оказывается полностью разрешимой и позволяет определить давление 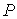 , внутреннюю энергию 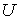 и энтропию 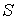 . В зависимости от выбора двух независимых параметров можно ввести термодинамические потенциалы, дифференцирование которых дает возможность определить другие, неизвестные параметры состояния. Рассмотрим несколько случаев.
1. Возьмем в качестве независимых параметров состояния объем 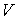 и энтропию 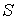 и запишем через эти переменные выражение для внутренней энергии 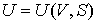 . . | (4.23) |
Тогда уравнение (4.20) можно представить в виде: 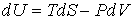 . . | (4.24) |
Учитывая правило нахождения полного дифференциала (см. например, формулы (4.6) и (4.7)), имеем 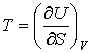 , , | (4.25) |
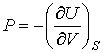 . . | (4.26) |
Эти формулы аналогичны выражениям для нахождения сил в механике через потенциальную энергию консервативной механической системы.
Таким образом, внутренняя энергия, выраженная через параметры состояния 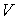 и 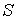 , является термодинамическим потенциалом. 2. Рассмотрим случай, когда независимыми параметрами состояния являются давление 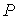 и энтропия 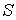 . Преобразуем уравнение (4.20) к виду 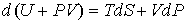 . . | (4.27) |
Введение функции состояния
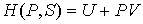 , , | (4.28) |
позволяет представить уравнение (4.27) в форме 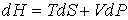 . . | (4.29) |
С учетом правила нахождения полного дифференциала 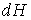 имеем 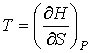 , , | (4.30) |
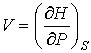 . . | (4.31) |
Функция 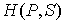 является термодинамическим потенциалом при независимых параметрах 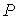 и 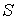 , и называется энтальпией. 3. Если в качестве независимых параметров выбрать объем 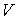 и температуру 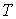 и уравнение (4.20) представить в виде 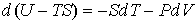 , , | (4.32) |
то функция состояния
 | (4.33) |
будет термодинамическим потенциалом.
Действительно, применяя правило нахождения полного дифференциала для выражения
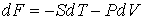 , , | (4.34) |
имеем
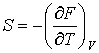 , , | (4.35) |
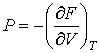 . . | (4.36) |
Термодинамический потенциал 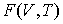 называется свободной энергией или потенциалом Гельмгольца. 4. При выборе в качестве независимых переменных давления 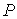 и температуры 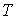 и введения функции состояния в форме 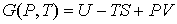 , , | (4.37) |
уравнение (4.27) может быть преобразовано к виду 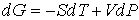 . . | (4.38) |
Так как 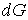 является полным дифференциалом, то имеем: 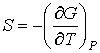 , , | (4.39) |
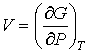 . . | (4.40) |
Функция 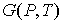 называется термодинамическим потенциалом Гиббса (энергией Гиббса). Между термодинамическими потенциалами могут быть установлены соотношения, позволяющие выразить одни потенциалы через другие. Подстановка выражения (4.35) в формулу (4.33) дает уравнение Гиббса-Гельмгольца: 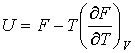 , , | (4.41) |
связывающее между собой внутреннюю энергию 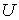 и свободную энергию 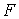 . 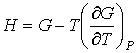 , , | (4.42) |
устанавливающее взаимосвязь энтальпии 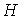 и потенциала Гиббса 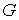 . Задача 4.3. Определить термодинамические потенциалы фотонного газа, если известны уравнение его состояния 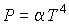 , выражение для внутренней энергии , выражение для внутренней энергии 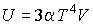 и энтропия и энтропия 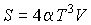 . .
Решение: Использование приведенных в условии задачи выражений для внутренней энергии 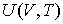 и энтропии и энтропии 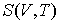 позволяет получить зависимость внутренней энергии позволяет получить зависимость внутренней энергии 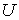 от параметров от параметров 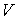 и и 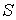 : :
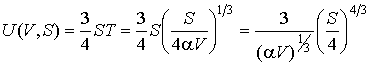 .
Аналогично найдем другие термодинамические потенциалы:
энтальпия:
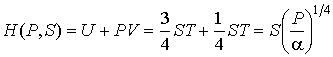 ;
свободная энергия:
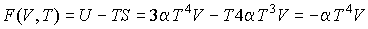 ,
потенциал Гиббса:
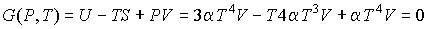 .
Равенство нулю потенциала Гиббса для фотонного газа делает невозможным использование этого потенциала при расчетах и связано с тем, что переменные 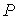 и и 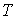 не являются независимыми, а связаны между собой однозначным соотношением не являются независимыми, а связаны между собой однозначным соотношением 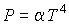 . .
|