3.7. Неравенство Клаузиуса
Совместное применение первой и второй теоремы Карно позволяет получить следующее неравенство:
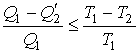 . . | (3.41) |
Знак равенства в этой формуле соответствует случаю описания обратимой тепловой машины, а знак меньше - описанию необратимой тепловой машины.
Формулу (3.41) можно преобразовать в виду 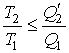 . . | (3.42) |
Выражение (3.42) в свою очередь дает 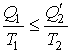 , , | (3.43) |
или
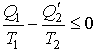 . . | (3.44) |
Если полученное выражение записать через количество теплоты, подводимой к рабочему телу от нагревателя 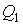 и холодильника 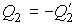 , то оно примет окончательную форму 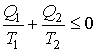 . . | (3.45) |
Формула (3.45) представляет собой частный случай неравенства Клаузиуса. Для получения неравенства Клаузиуса в общем случае рассмотрим тепловую машину, рабочее тело которой при совершении кругового термодинамического процесса обменивается теплотой с достаточно большим числом тепловых резервуаров, имеющих температуры 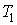 ,  ,..., 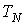 . При этих теплообменах рабочее тело получает от тепловых резервуаров теплоты 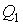 ,  ,..., 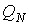 . Работа такой тепловой машины будет равна: 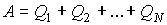 . При использовании этого выражения необходимо учитывать, что теплоты 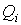 могут иметь отрицательный знак в случае, если в при теплообмене с 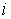 -тым резервуаром теплота отбирается от рабочего тела. Применительно к рассматриваемой тепловой машине неравенство (3.45) может быть записано в виде 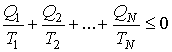 , , | (3.46) |
или
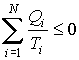 . . | (3.47) |
Величина 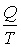 называется приведенным количеством теплоты, и она равна количеству теплоты, полученной системой, при абсолютной температуре 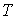 , деленной на эту температуру. При переходе к бесконечному числу тепловых резервуаров, с которыми рабочее тело тепловой машины обменивается теплотой, суммирование в формуле (3.47) может быть заменено интегрированием по замкнутому термодинамическому циклу: 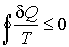 . . | (3.48) |
Из этой формулы следует, что сумма приведенных количеств теплоты на замкнутом цикле для любой термодинамической системы не может быть больше нуля. Неравенство (3.48) было получено в 1862 году Клаузиусом и носит его имя. Неравенство Клаузиуса позволяет отличать обратимые и необратимые круговые термодинамические процессы. В случае, если термодинамический цикл состоит только из обратимых процессов (изотермических и адиабатических), неравенство (3.48) переходит в равенство Клаузиуса 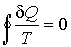 , , | (3.49) |
имеющее принципиальное значение для построения равновесной термодинамики.
Случай строгого неравенства в формуле (3.48) соответствует описанию необратимых круговых термодинамических процессов, и это выражение применяется в неравновесной термодинамике.
|