|
|
|||
|
|||
|
ГЛАВА 6
6.5. Производство энтропии в необратимых процессах |
|
При протекании необратимых термодинамических процессов происходит возрастание энтропии. Производство энтропии
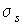 в единичном объеме при протекании в единичном объеме при протекании 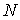 различных процессов можно вычислить с помощью выражения (4.78), полученного в параграфе 4.5: различных процессов можно вычислить с помощью выражения (4.78), полученного в параграфе 4.5:
где:
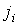 - плотности термодинамических потоков, - плотности термодинамических потоков, 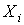 - соответствующие им термодинамические силы. Тогда производство энтропии внутри выделенного объема среды - соответствующие им термодинамические силы. Тогда производство энтропии внутри выделенного объема среды 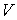 определяется с помощью формулы определяется с помощью формулы
Получим выражения, позволяющие рассчитывать производство энтропии при протекании рассмотренных выше необратимых процессов в газах: переноса теплоты (теплопроводности) и переноса импульса (вязкости). В соответствии с полученными в параграфе 6.2 выражениями, плотности термодинамических потоков в указанных процессах имеют вид:
где:
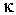 и и 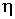 - коэффициенты теплопроводности и вязкости, - коэффициенты теплопроводности и вязкости, 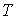 и и 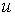 - температура и скорость течения газа соответственно. - температура и скорость течения газа соответственно.Для рассматриваемого случая линейной термодинамики без учета взаимного влияния процессов соотношение между термодинамическими силами и потоками имеет линейную зависимость
где
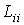 - кинетические коэффициенты, пропорциональные введенным выше коэффициентам теплопроводности и вязкости. Они имеют вид: - кинетические коэффициенты, пропорциональные введенным выше коэффициентам теплопроводности и вязкости. Они имеют вид:
Тогда выражения для термодинамических сил примут форму:
а соответствующие формулы для расчета производства энтропии принимают вид
Анализ полученных выражений показывает, что при протекании необратимых процессов теплопроводности и вязкости производство энтропии является положительной величиной. Если газ находится в равновесном состоянии, которое характеризуется постоянством параметров состояния (в данном случае, если
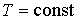 и и 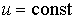 ), то в такой среде будут отсутствовать термодинамические потоки и производство энтропии станет равным нулю. ), то в такой среде будут отсутствовать термодинамические потоки и производство энтропии станет равным нулю.Задача 6.3. Определить производство энтропии в газе, находящимся между двумя плоскими стенками, имеющими температуры
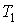 и и 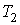 . Считать, что расстояние между стенками . Считать, что расстояние между стенками 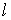 много меньше линейных размеров стенок. много меньше линейных размеров стенок.Решение: Так как поток теплоты во всех точках (пренебрегая краевыми эффектами) между близко расположенными друг к другу стенками должен быть одинаковым, то в установившемся режиме на основании выражения (6.23) можно записать:
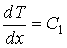 или после интегрирования
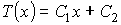 , ,где константы
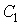 и и 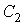 могут быть определены из граничных условий могут быть определены из граничных условий 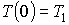 и и 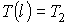 . Тогда имеем: . Тогда имеем: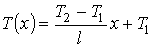 , ,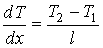 . .Подстановка этих выражений в формулу (6.58) дает
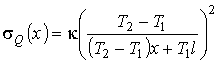 . .Из полученного выражения следует, что в разных точках газа производство энтропии различно.
Производство энтропии внутри всего газа, расположенного между стенками, можно вычислить с помощью формулы (6.50):
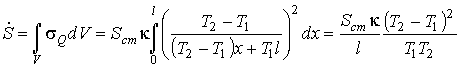 , ,где
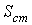 - площадь поверхности стенки. - площадь поверхности стенки.Такой же результат можно получить и воспользовавшись для определения производства энтропии непосредственно выражением (3.52):
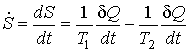 , ,где
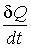 - поток теплоты - поток теплоты 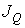 , взятый с обратным знаком: , взятый с обратным знаком: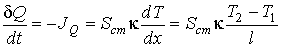 . .Подстановка этого выражения в предыдущую формулу позволяет получить следующую формулу
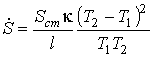 , ,которая полностью совпадает с выражением, полученным выше первым способом.
|
|
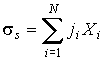 ,
,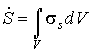 .
.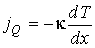 ,
,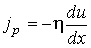 ,
,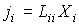 ,
,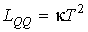 ,
,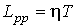 .
.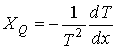 ,
,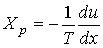 ,
,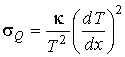 ,
,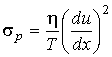 .
.