|
|
|||
|
|||
|
ГЛАВА 4
4.3. Применение термодинамических потенциалов |
|
Рассмотрим применение метода термодинамических потенциалов для описания эффекта Джоуля-Томсона. Этот эффект заключается в изменении температуры газа при его медленном пропускании через пористую перегородку.
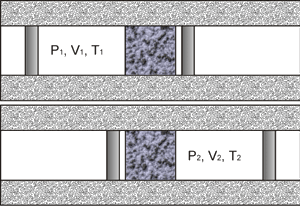
Пусть газ, имевший давление 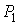 , объем , объем 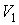 и температуру и температуру 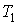 , адиабатически расширился при прохождении через пористую перегородку и приобрел давление , адиабатически расширился при прохождении через пористую перегородку и приобрел давление 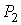 , объем , объем 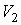 и температуру и температуру 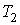 (см. рис. 4.1). При этом давления (см. рис. 4.1). При этом давления 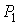 и и 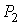 в обеих частях сосуда будем считать постоянными. В опыте Джоуля-Томсона это обеспечивается тем, что хотя процесс протекания газа через пористую перегородку будет неравновесным, но вследствие медленности его течения, газ по обе стороны от перегородки можно считать находящимся в равновесии. Сосуд адиабатически изолирован от окружающей среды. Пористая перегородка также обеспечивает изолированность двух частей сосуда друг от друга. в обеих частях сосуда будем считать постоянными. В опыте Джоуля-Томсона это обеспечивается тем, что хотя процесс протекания газа через пористую перегородку будет неравновесным, но вследствие медленности его течения, газ по обе стороны от перегородки можно считать находящимся в равновесии. Сосуд адиабатически изолирован от окружающей среды. Пористая перегородка также обеспечивает изолированность двух частей сосуда друг от друга.
При равновесном адиабатическом расширении температура газа изменяется в соответствии с уравнением адиабаты. Для идеального газа эта зависимость имеет вид (см. формулу (2.86)):
Таким образом, при равновесном адиабатическом расширении идеального газа происходит изменение его температуры. Покажем, что при неравновесном адиабатическом расширении использование выражения (4.43) для определения температуры идеального газа, прошедшего через пористую перегородку, становится невозможным.
Проведем описание процесса протекания газа через пористую перегородку. Считая этот процесс достаточно медленным и адиабатическим, а также, учитывая постоянство давлений
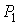 и и 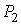 , применим первое начало термодинамики: , применим первое начало термодинамики:
или учитывая определение энтальпии (4.28)
Следовательно, рассматриваемый процесс является не только адиабатическим, но и изоэнтальпийным.
Далее будем считать, что изменение давления
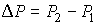 и температуры и температуры 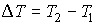 газа в рассматриваемом процессе малы. Тогда с точностью до величин второго порядка малости можно записать: газа в рассматриваемом процессе малы. Тогда с точностью до величин второго порядка малости можно записать:
Следовательно:
Для определения частных производных энтальпии
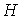 найдем полный дифференциал от выражения (4.28) найдем полный дифференциал от выражения (4.28)
Тогда с учетом формулы (4.46) имеем:
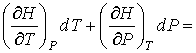
Из этой формулы следует:
где
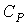 - теплоемкость газа при постоянном давлении. При получении выражения (4.50) использована формула (1.5) с учетом выражения (1.12), а при получении формулы (4.51) - уравнение (4.24). - теплоемкость газа при постоянном давлении. При получении выражения (4.50) использована формула (1.5) с учетом выражения (1.12), а при получении формулы (4.51) - уравнение (4.24). Дифференцирование выражения (4.39) по давлению
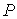 , а формулы (4.40) по температуре , а формулы (4.40) по температуре 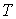 , с учетом равенства перекрестных производных потенциала Гиббса , с учетом равенства перекрестных производных потенциала Гиббса
дает
Подстановка выражения (4.53) в формулу (4.51) и далее, с ее учетом формул (4.50) и (4.51), в выражение (4.47) позволяет получить следующее соотношение:
где производная
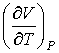 определяется уравнением состояния газа. Формула (4.54) позволяет рассчитать изменение температуры газа при просачивании его через пористую перегородку. определяется уравнением состояния газа. Формула (4.54) позволяет рассчитать изменение температуры газа при просачивании его через пористую перегородку.Если при проведении опыта использовать идеальный газ, описываемый уравнением Клапейрона-Менделеева (2.10), то имеем:
Следовательно, для идеального газа
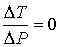 и изменения его температуры при прохождении через пористую перегородку не происходит. и изменения его температуры при прохождении через пористую перегородку не происходит.Таким образом, при неравновесном прохождении идеального газа через пористую перегородку его температура не изменяется, в отличие от равновесного адиабатического расширения, приводящего в соответствии с формулой (4.43) к охлаждению идеального газа.
Данный результат связан с тем, что при расширении идеального газа в опыте Джоуля-Томсона механическая работа не совершается, в отличие от равновесного адиабатического расширения. При применении в этом опыте реального газа совершаемая им механическая работа определяется силами межмолекулярного взаимодействия, и её знак зависит от этих сил.
Рассмотрим применение в опыте Джоуля-Томсона газа Ван-дер-Ваальса, уравнение (2.117) для одного моля которого имеет вид:
Раскроем скобки в этом уравнении
и пренебрегая третьим и четвертым слагаемыми в левой части получившегося выражения в связи с их малостью (считая
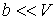 ), продифференцируем его по температуре ), продифференцируем его по температуре 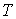 при постоянном давлении при постоянном давлении 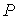 : :
или
Выражая
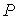 из формулы (4.56) и подставляя в (4.59) с последующим пренебрежением малыми слагаемыми имеем: из формулы (4.56) и подставляя в (4.59) с последующим пренебрежением малыми слагаемыми имеем:
Тогда формула (4.54) для отношения
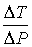 принимает вид принимает вид
Из этой формулы следует, что если
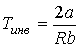 , то не происходит изменение температуры Ван-дер-Ваальсовского газа при его прохождении через пористую перегородку. Эта температура , то не происходит изменение температуры Ван-дер-Ваальсовского газа при его прохождении через пористую перегородку. Эта температура 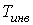 называется температурой инверсии. При называется температурой инверсии. При 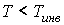 отношение отношение 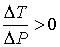 и наблюдается охлаждение газа (так как и наблюдается охлаждение газа (так как 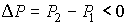 ), а при ), а при 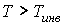 отношение отношение 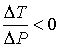 и газ нагревается. В первом случае эффект Джоуля-Томсона считается положительным, а во втором - соответственно отрицательным. и газ нагревается. В первом случае эффект Джоуля-Томсона считается положительным, а во втором - соответственно отрицательным.Другим примером применения термодинамических потенциалов является расчет поверхностного натяжения и его зависимости от температуры.
При описании поверхностного натяжения площадь поверхности
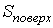 является таким же параметром состояния, как и объем является таким же параметром состояния, как и объем 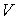 . Тогда использование формулы (4.34) для дифференциала свободной энергии (термодинамического потенциала Гельмгольца) . Тогда использование формулы (4.34) для дифференциала свободной энергии (термодинамического потенциала Гельмгольца) 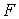 позволяет получить выражение: позволяет получить выражение:
где последнее слагаемое характеризует вклад поверхностного натяжения. Величина
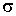 называется коэффициентом поверхностного натяжения и он численно равен работе при изменении площади поверхности на единицу. называется коэффициентом поверхностного натяжения и он численно равен работе при изменении площади поверхности на единицу.Пусть имеется система, состоящая из жидкости, описываемой параметрами
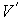 и и 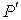 , пара, с параметрами , пара, с параметрами 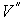 и и 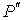 , и границы их раздела. Будем считать, что общий объем жидкости и пара постоянен: , и границы их раздела. Будем считать, что общий объем жидкости и пара постоянен: 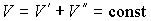 , и их температуры одинаковы: , и их температуры одинаковы: 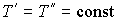 . Тогда дифференциал . Тогда дифференциал 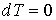 , и для такой системы дифференциал свободной энергии , и для такой системы дифференциал свободной энергии 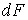 принимает вид: принимает вид:
В условиях равновесия
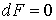 имеем имеем
Если поверхность сферическая, то
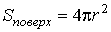 , , 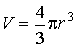 и, следовательно: и, следовательно:
В случае, если поверхность имеет произвольную форму и характеризуется двумя главными радиусами
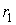 и и 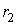 , то: , то:
Выражение (4.67) носит названия формулы Лапласа для поверхностного натяжения. При
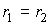 выражение (4.67) переходит в (4.66). выражение (4.67) переходит в (4.66).Термодинамический потенциал Гельмгольца (4.62) позволяет определить также зависимость коэффициента поверхностного натяжения
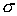 от температуры от температуры 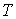 . Будем считать, что давление жидкости . Будем считать, что давление жидкости 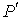 и пара и пара 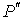 поддерживаются одинаковыми: поддерживаются одинаковыми: 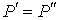 . Тогда с учетом того, что . Тогда с учетом того, что 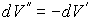 имеем выражение для свободной энергии в виде: имеем выражение для свободной энергии в виде:
Из этого выражения следует
Если ввести теплоту изотермического образования единицы поверхности
то формула (4.69) примет вид:
Интегрирование этого выражения при условии
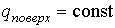 и и 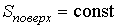 дает дает
где
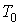 и и 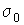 - константы, зависящие от физических свойств жидкости и пара. - константы, зависящие от физических свойств жидкости и пара.Таким образом, коэффициент поверхностного натяжения имеет логарифмическую зависимость от температуры.
|
|
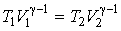 .
.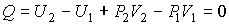
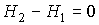 .
.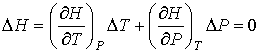 .
.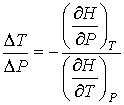 .
.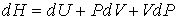 .
.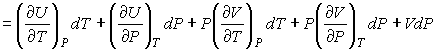 .
.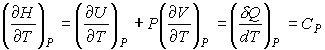 ,
,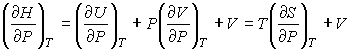 .
.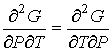
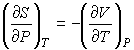 .
.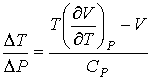 ,
,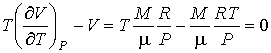 .
.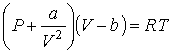 .
.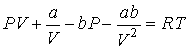
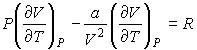
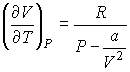 .
.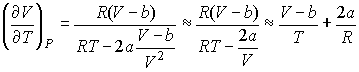 .
.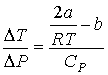 .
.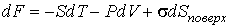 ,
,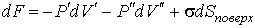 .
.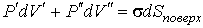 .
.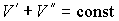 , то
, то 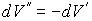 . Тогда выражение
. Тогда выражение 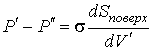 .
.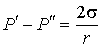 .
.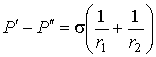 .
.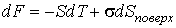 .
.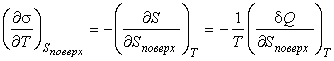 .
.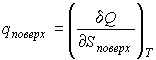 ,
,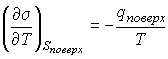 .
.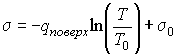 ,
,