Рассмотрим уравнение вида ![]() .
.
Это уравнение равносильно по системе:
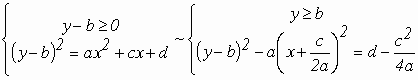
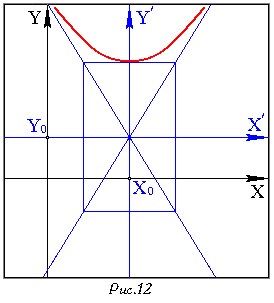 Если
Если 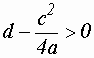 и
и
![]() , то уравнение:
, то уравнение:
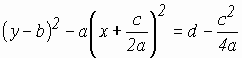 задает ту часть гиперболы, которая лежит в полуплоскости
задает ту часть гиперболы, которая лежит в полуплоскости
![]() .
.
Строим ту часть гиперболы, которая выше прямой
![]() .
.
П.V.1(2).
 Если
Если 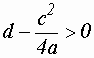 , а
, а
![]() , то уравнение:
, то уравнение:
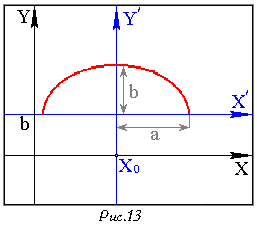
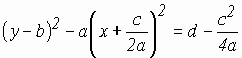 задает ту часть эллипса, которая лежит в полуплоскости
задает ту часть эллипса, которая лежит в полуплоскости
![]() .
.
Строим ту часть эллипса которая лежит выше прямой
![]() .
.
П.V.1(3).
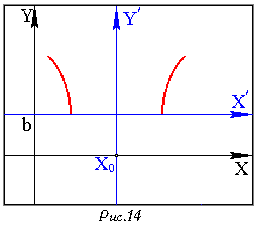 Если
Если 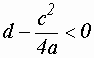 и
и
![]() , уравнение
, уравнение
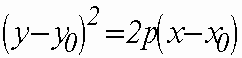
задает ту часть гиперболы, которая лежит в полуплоскости
![]() .
.
П.V.1(4).
Если 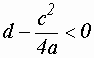 и
и
![]() , то уравнение
, то уравнение
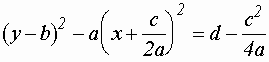 - задает мнимый эллипс.
- задает мнимый эллипс.
П.V.1(5).
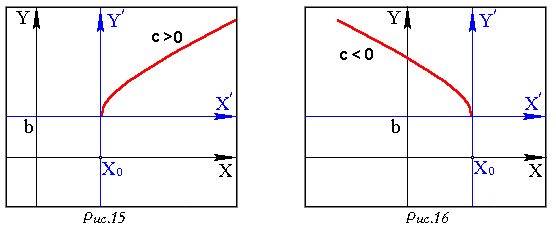
Если ![]() , то уравнение
, то уравнение
![]() равносильно системе
равносильно системе
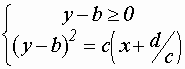 задает ту часть параболы,
которая лежит в полуплоскости
задает ту часть параболы,
которая лежит в полуплоскости ![]() .
.
П.V.1(6).
Если 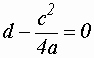 и
и ![]() , то уравнение
, то уравнение
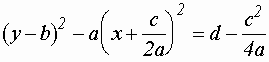 задает пару пересекающихся прямых
задает пару пересекающихся прямых
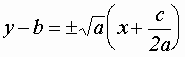 , которые лежат в полуплоскости
, которые лежат в полуплоскости
![]() .
.
П.V.1(7).
Если 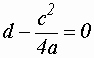 и
и
![]() , то уравнение
, то уравнение
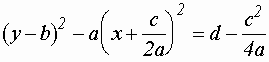 задает точку
задает точку
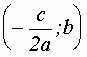 , при условии, что она лежит в полуплоскости
, при условии, что она лежит в полуплоскости
![]() .
.
П.V.2.
Рассмотрим уравнение вида ![]() .
.
Это уравнение равносильно системе, т.к. рассматриваются только положительные значения корня.
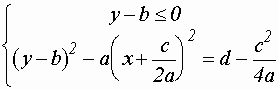 .
.
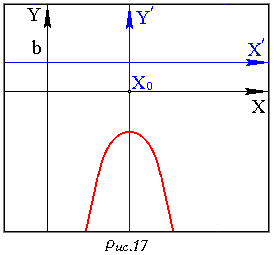 Если
Если 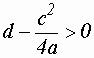 и
и
![]() , то уравнение
, то уравнение
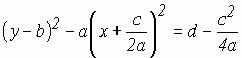 задает ту часть гиперболы, которая лежит в полуплоскости
задает ту часть гиперболы, которая лежит в полуплоскости
![]() .
.
П.V.2(2).
 Если
Если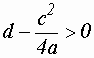 , а
, а
![]() , то уравнение
, то уравнение
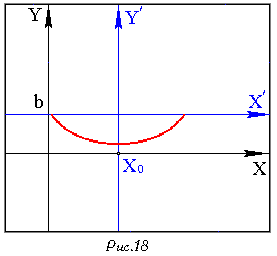
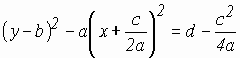 задает ту часть эллипса, которая лежит в полуплоскости
задает ту часть эллипса, которая лежит в полуплоскости
![]() .
.
П.V.2(3).
 Если
Если 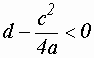 , а
, а
![]() , то уравнение
, то уравнение
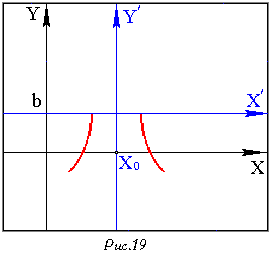
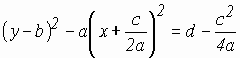 задает ту часть гиперболы,которая лежит в полуплоскости
задает ту часть гиперболы,которая лежит в полуплоскости
![]()
П.V.2(4).
Если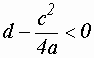 и
и![]() , то уравнение
, то уравнение
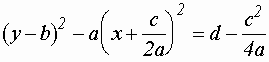 задает мнимый эллипс.
задает мнимый эллипс.
П.V.2(5).
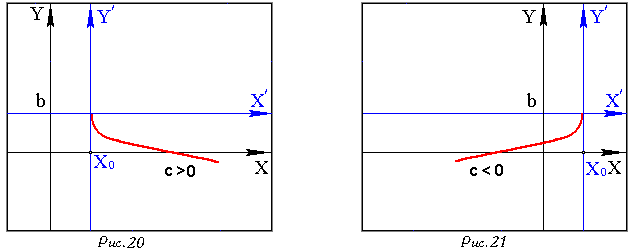
Если ![]() , то уравнение
, то уравнение
![]() равносильно системе:
равносильно системе:
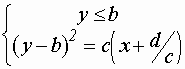 , которая задает ту часть параболы, которая лежит в полуплоскости
, которая задает ту часть параболы, которая лежит в полуплоскости
![]() .
.
П.V.2(6).
Если 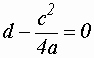 и
и
![]() , то уравнение
, то уравнение
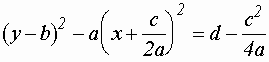 задает пару пересекающихся прямых
задает пару пересекающихся прямых
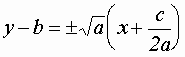 , которые лежат в полуплоскости
, которые лежат в полуплоскости
![]() .
.
П.V.2(7).
Если 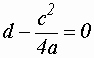 и
и
![]() , то уравнение
, то уравнение
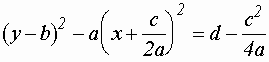 задает точку
задает точку
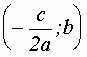 при условии, что она лежит в полуплоскости
при условии, что она лежит в полуплоскости
![]() .
.