П.IV.1. Для исследования кривых второго порядка,
общее уравнение которых имеет вид
![]() , рассматривается произведение
, рассматривается произведение
![]() .
.
В процессе исследования кривых 2-го порядка, уравнение которых записано в общем виде, полезна "процедура выделения полного квадрата". Выделяем полный квадрат уравнения
![]() получим:
получим:
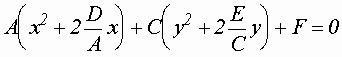 или
или
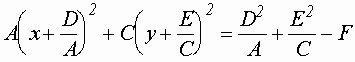 ,
,
обозначим: 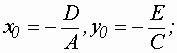
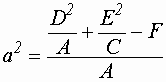 ;
;
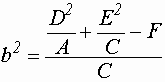 .
.
Если ![]() , то уравнение задает кривую эллиптического типа. Причем:
, то уравнение задает кривую эллиптического типа. Причем:
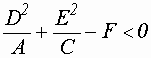 - мнимый эллипс.
- мнимый эллипс.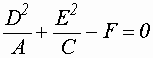 - точка
- точка
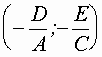 .
.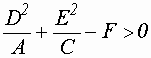 , то имеем
, то имеем
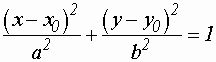 - канонический вид эллипса.
- канонический вид эллипса.
Если ![]() , то уравнение задает кривую
гиперболического типа. Причем:
, то уравнение задает кривую
гиперболического типа. Причем:
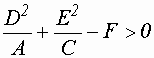 , или
, или
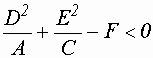 имеем:
имеем: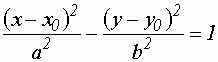 или
или
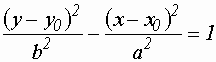 - канонический вид гиперболы.
- канонический вид гиперболы.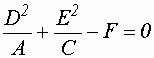 и учитывая знаки
и учитывая знаки
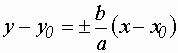 - пара пересекающихся прямых.
- пара пересекающихся прямых.Если:
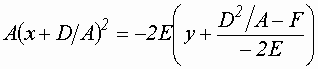 .Обозначим:
.Обозначим:
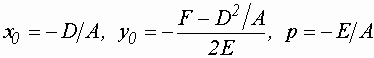 имеем:
имеем: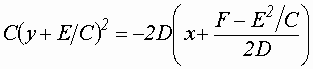 .Обозначим:
.Обозначим:
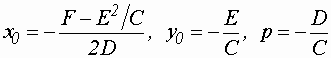 - имеем:
- имеем: