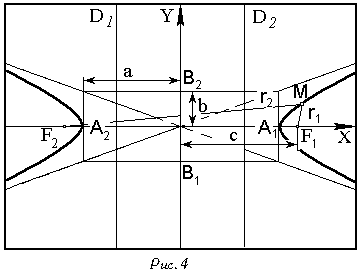
Определение:гиперболой называется множество точек плоскости, абсолютная величина разности которых до двух данных точек, называемых фокусами, есть величина постоянная (ее обозначают через ), причем эта постоянная меньше расстояния между фокусами .

Если поместить фокусы гиперболы в точках и , то получится каноническое уравнение гиперболы где .

Точки: и называются вершинами гиперболы. Отрезок такой, что , называется действительной осью гиперболы, а отрезок такой, что - мнимой осью.

Гипербола имеет две асимптоты, уравнения которых .

Отношение называется эксцентриситетом гиперболы.

Уравнение также является уравнением гиперболы, но действительной осью этой гиперболы служит отрезок оси длины .

Две гиперболы и имеют одни и те же полуоси и одни и те же асимптоты, но действительная ось одной служит мнимой осью другой, и наоборот. Такие две гиперболы называются сопряженными.

Прямые и , перпендикулярные действительной оси и проходящие на расстоянии от центра, называются директрисами гиперболы.

П.II.1 Расположение гиперболы.

1)  ;	2)  ;
- центр,,	- центр,,

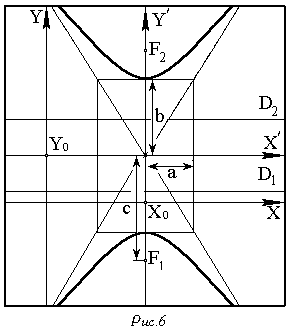1); -эксцентриситет.

2); - эксцентриситет.

1); .

2); .

П.II.4 .

- уравнение асимптот гиперболы.

Назад |  В начало |  Дальше