3.4. Фазовые переходы второго рода
Описание фазовых переходов второго рода проведем в соответствии с методом, предложенным в 1933 году физиком-теоретиком Эренфестом. Для таких переходов уравнение Клапейрона-Клаузиуса не применимо, так как из условия равенства первых производных удельного термодинамического потенциала
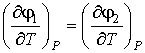 , , | (3.28) |
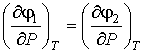 | (3.29) |
в соответствии с формулами (2.52) и (2.53) следует равенство удельных энтропий и объемов
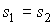 , , | (3.30) |
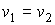 . . | (3.31) |
Это приводит к тому, что в правой части уравнения (3.22) одновременно обращаются в нуль числитель и знаменатель, и в уравнении Клапейрона-Клаузиуса возникает неопределенности вида 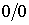 .
Найдем полные дифференциалы удельных энтропий и объемов, и в соответствии с формулами (3.30) и (3.31) приравняем их
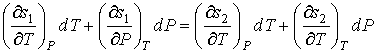 , , | (3.32) |
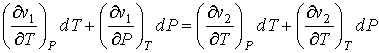 . . | (3.33) |
Проведем преобразование полученных выражений. Производная удельной энтропии по температуре в обратимом процессе может быть представлена в виде
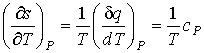 , , | (3.34) |
где: 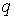 - удельная теплота, 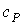 - удельная изобарическая теплоемкость.
Так как для второй производной удельного термодинамического потенциала может быть записано равенство
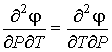 , , | (3.35) |
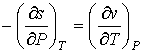 . . | (3.36) |
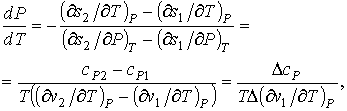 | (3.37) |
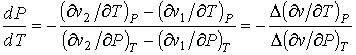 , , | (3.38) |
где символом 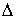 обозначена операция нахождения разности соответствующих величин.
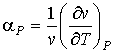 | (3.39) |
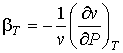 . . | (3.40) |
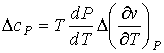 , , | (3.41) |
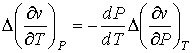 . . | (3.42) |
Отметим, что при фазовом переходе второго рода все свойства вещества изменяются непрерывным образом во всем объеме вещества. Поэтому при фазовых переходах второго рода невозможно существование метастабильных состояний, характерных для фазовых переходов первого рода.
|