3.3. Фазовые переходы первого рода
Для описания фазового перехода первого рода необходимо определить зависимость давления от температуры в точках фазового перехода: 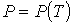 , то есть форму кривой равновесия двух фаз. Применение методов равновесной термодинамики позволяет определить первую производную этой зависимости, или наклон кривой равновесия.
Для этого вычислим полные дифференциалы от правой и левой частей выражения (3.4)
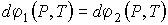 | (3.20) |
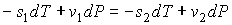 , , | (3.21) |
где: 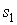 и 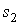 - удельные энтропии первой и второй фаз соответственно.
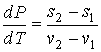 . . | (3.22) |
Так как процесс перехода вещества из одной фазы в другую считается равновесным и происходящим при постоянной температуре, то разность удельных энтропий этих фаз можно определить следующим образом
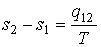 . . | (3.23) |
Подстановка этого выражения в формулу (3.22) приводит её к виду:
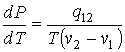 . . | (3.24) |
Это выражение называется уравнением Клапейрона-Клаузиуса. Оно позволяет определить производную давления от температуры при равновесном фазовом переходе первого рода в зависимости от удельной теплоты перехода, его температуры и удельных объемов начальной и конечной фаз.
В соответствии с уравнением Клапейрона-Клаузиуса знак производной 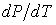 зависит от соотношения удельных объем фаз. Если при подводе теплоты жидкость переходит в газообразное состояние, что сопровождается увеличением удельного объема: 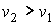 , то производная 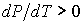 . Поэтому при таком переходе повышение давления приводит к увеличению температуры кипения. Аналогичная зависимость наблюдается и при плавлении большинства твердых тел. Исключение составляют вещества, для которых плавление сопровождается уменьшением их удельного объема: 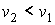 . Примером такого вещества является вода, которая при переходе из замерзшего состояния в жидкое уменьшает свой удельный объем (плотность воды больше плотности льда). Для таких веществ характерно понижение температуры плавления при повышении давления.
Рассмотрим случай термодинамической системы, в которой в равновесии находятся сразу три фазы однородного по физико-химическим свойствам вещества. Равновесие такой системы будет наблюдаться при одновременном выполнении трех условий, соответствующих равновесию этих фаз между собой. Эти условия в общем виде можно записать в форме
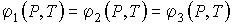 . . | (3.25) |
Равенства (3.25) приводят к системе из двух независимых уравнений
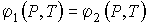 , , | (3.26) |
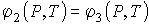 . . | (3.27) |
Решение этой системы уравнений при условии отсутствия химических превращений дает совершенно определенные значения давления 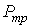 и температуры 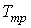 , при которых три фазы могут существовать одновременно. Точка на диаграмме состояния в переменных 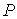 и 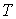 (см. рис. 3.1), соответствующая указанным значениям давления и температуры, называется тройной точкой. В этой точке встречаются кривая плавления 1, разделяющая твердую и жидкую фазы, кривая испарения 2, разделяющая жидкую и газообразную фазы, и кривая возгонки 3, разделяющая твердую и газообразную фазы. | Рис. 3.1.
Диаграмма состояния: 1 – кривая плавления, 2 – кривая испарения, 3 – кривая возгонки |
Кривая испарения 2 заканчивается критической точкой (К), в которой исчезают отличия жидкой и газообразной фаз. Если фазовый переход осуществляется в обход критической точки, как показано пунктирной линией на рис. 3.1, то пересечения кривой испарения не происходит и фазовое превращение проходит путем непрерывных изменений без образования границы раздела фаз.
Для однородного по своим физико-химическим свойствам вещества в равновесии одновременно могут находиться не более трех фаз. Это означает, что для равновесной системы могут существовать только точки, в которых сходятся три фазы вещества, например, соответствующие трем его агрегатным состояниям. Точки, в которых могли бы одновременно существовать более трех фаз, не реализуемы.
Как правило, все твердые вещества имеют несколько фазовых состояний, обусловленных различными кристаллическими модификациями, структурно отличающимися между собой. Эти фазы могут точно так же находиться в состоянии равновесия между собой, как и фазы, связанные с различными агрегатными состояниями. На диаграмме состояния условиям равновесия этих фаз соответствуют кривые равновесия при фазовых переходах. Существуют тройные точки, в которых могут одновременно находиться в равновесии три фазы, две из которых представляют собой кристаллические модификации, а одна либо жидкая, либо газообразная. У некоторых веществ тройные точки наблюдаются при равновесии трех различных кристаллических модификаций.
Метастабильные состояния системы жидкость-газ наблюдаются в областях параметров, близких к кривой испарения. С повышением температуры плотность насыщенного пара возрастает и при некоторой температуре плотность пара становится равной плотности жидкости. Температура, при которой это происходит, называется температурой абсолютного кипения. При этом исчезает различие между жидкой и газообразной фазами, и кривая испарения заканчивается критической точкой К (см. рис. 3.1). Такое состояние, которое характеризуется определенным набором значений температуры 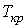 , давления 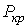 и объема 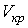 , получило название критического состояния.
При температурах выше критической происходит постепенный переход одной фазы в другую без образования двухфазной системы. В этом случае переход из жидкого состояния в газообразное (или, наоборот, из газообразного в жидкое) может быть осуществлен по траектории, огибающей критическую точку без пересечения кривой испарения (пунктирная линия на рис. 3.1). При этом фазового перехода первого рода с характерным для него скачком первых производных удельного термодинамического потенциала наблюдаться не будет. Переход из жидкого в газообразное состояние будет происходить путем непрерывных изменений без образования границы раздела фаз. Такая среда будет представлять собой однородную структуру, которая постепенно превращается из жидкости в газ или наоборот. То есть свойства фазы в этом случае меняются непрерывным образом.
|