3.2. Явления на границе раздела фаз
Проведем теоретическое описание явления поверхностного натяжения с помощью метода термодинамических потенциалов, рассмотренного в параграфе 2.2. В первой главе нами было получено выражение (1.10), позволяющее определить механическую работу, которая совершается при движении границы раздела жидкости и газа. Однако это выражение не учитывает работу сил межмолекулярного взаимодействия (сил поверхностного натяжения), которая необходима для создания единицы площади поверхности раздела фаз. Учет этой работы приводит к следующему выражению для полной механической работы, совершаемой при движении границы раздела
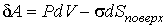 , , | (3.8) |
где величина 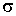 описывает поверхностное натяжение на границе раздела фаз.
Тогда, с учетом работы сил межмолекулярного взаимодействия, в формулу (2.35) для дифференциала свободной энергии (термодинамического потенциала Гельмгольца) 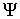 необходимо добавить новое слагаемое, которое описывает вклад поверхностного натяжения:
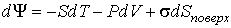 . . | (3.9) |
Как следует из этого выражения, при описании поверхностного натяжения площадь поверхности 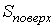 является таким же параметром состояния, как и объем 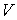 .
Пусть имеется система, состоящая из жидкости, описываемой параметрами 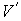 и 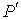 , газа, с параметрами 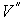 и 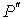 , и границы их раздела. Будем считать, что общий объем жидкости и газа постоянен: 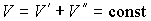 , и их температуры одинаковы: 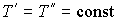 . Тогда дифференциал 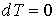 , и для такой системы дифференциал свободной энергии 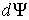 принимает вид:
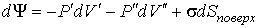 . . | (3.10) |
В условиях равновесия 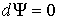 имеем
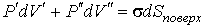 . . | (3.11) |
Так как 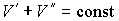 , то 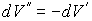 . Тогда выражение (3.11) можно преобразовать к виду:
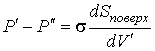 . . | (3.12) |
Если поверхность сферическая, то 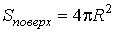 , 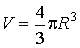 и, следовательно:
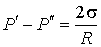 . . | (3.13) |
В случае, если поверхность имеет произвольную форму и характеризуется двумя главными радиусами 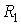 и 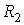 , то:
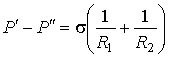 . . | (3.14) |
Если поверхность жидкости имеет цилиндрическую форму, то один из радиусов в формуле (3.14) становится бесконечным, и для этого случая формула (3.14) приобретает вид
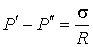 , , | (3.15) |
где: 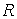 - радиус цилиндрической поверхности жидкости.
Термодинамический потенциал Гельмгольца (3.9) позволяет также определить зависимость поверхностного натяжения 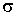 от температуры 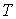 . Будем считать, что давление жидкости 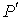 и газа 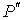 поддерживаются одинаковыми: 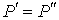 . Тогда с учетом того, что 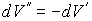 имеем выражение для свободной энергии в виде:
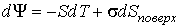 . . | (3.16) |
Из этого выражения следует
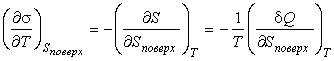 . . | (3.17) |
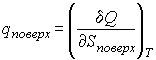 , , | (3.18) |
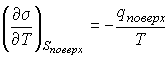 . . | (3.19) |
Как показывает опыт, теплота изотермического образования единицы поверхности 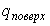 является положительной величиной. Поэтому поверхностное натяжение 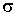 уменьшается с повышением температуры, причем быстрота этого уменьшения обратно пропорциональна абсолютной температуре.
|