2.5. Введение в термодинамику необратимых процессов
Применение законов равновесной термодинамики ограничено случаем, когда температура 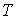 , давление 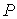 и другие параметры состояния во всех точках системы одинаковы. Если это не так, то в термодинамической системе возникают необратимые процессы.
Для описания необратимых процессов можно воспользоваться гипотезой локального равновесия, заключающейся в предположении, что внутри малого объема среды выполняется основное уравнение термодинамики равновесных процессов. Если в качестве параметров состояния ввести удельную плотность внутренней энергии 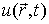 , приходящуюся на единицу массы среды, и удельный объем 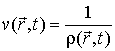 , где 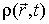 - плотность среды, то для точки среды с координатами 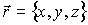 в момент времени 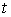 можно записать уравнение
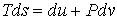 . . | (2.82) |
Здесь 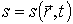 - удельная энтропия на единицу массы среды.
Тогда внутренняя энергия 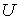 всей системы определяется с помощью выражения
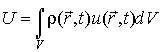 , , | (2.83) |
а ее энтропия 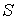 соответственно может быть найдена по формуле
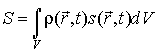 . . | (2.84) |
Совместное применение уравнения (2.82) с уравнениями баланса массы, внутренней энергии и других термодинамических величин, позволяет построить феноменологическую термодинамику необратимых процессов, опирающуюся на использование полученных из опыта соотношений между параметрами, описывающими термодинамические процессы.
Ключевое значение в термодинамике необратимых процессов имеет величина, численно равная скорости увеличения энтропии в единице объема:
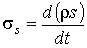 . . | (2.85) |
Если в качестве термодинамических параметров системы выступают 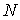 величин 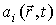 , то формулу (2.85) можно представить в виде:
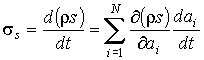 . . | (2.86) |
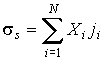 . . | (2.87) |
В случае небольших отклонений от равновесного состояния между термодинамическими потоками 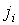 и термодинамическими силами 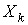 может быть установлена линейная зависимость
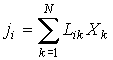 . . | (2.88) |
Таким образом, для линейных необратимых процессов производство энтропии определяется выражением
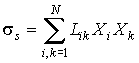 | (2.89) |
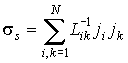 . . | (2.90) |
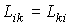 , , | (2.91) |
Принцип минимума производства энтропии позволяет установить критерий отбора реализующихся в природе необратимых процессов от реально не наблюдающихся, и, таким образом, выбрать из возможных процессов реально существующие.
Необходимость выполнения указанного принципа приводит к тому, что при протекании в среде необратимых стационарных процессов возникают динамические структуры, названные Пригожиным диссипативными структурами, что уменьшает производство энтропии. Примером таких структур могут служить ячейки Бенара – регулярные динамические структуры, возникающие в тонком слое нагреваемой снизу жидкости, и колебательные химические реакции Б.П. Белоусова, при которых происходят периодические изменения концентрации реагирующих веществ.
Проведем расчет производства энтропии при переносе теплоты и импульса. Производство энтропии внутри выделенного объема среды 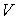 определяется с помощью формулы
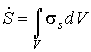 , , | (2.92) |
где 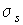 рассчитывается по формуле (2.87).
Получим выражения, позволяющие рассчитывать производство энтропии при протекании рассмотренных выше необратимых процессов в газах. В этом случае плотности термодинамических потоков переноса теплоты и импульса имеют вид:
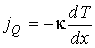 , , | (2.93) |
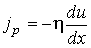 , , | (2.94) |
где: 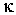 и 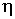 - коэффициенты теплопроводности и вязкости, 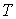 и 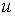 - температура и скорость течения газа соответственно.
Для рассматриваемого случая термодинамики линейных необратимых процессов без учета взаимного влияния различных процессов друг на друга соотношение между термодинамическими силами и потоками имеет линейную зависимость
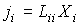 , , | (2.95) |
где 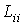 - кинетические коэффициенты, пропорциональные введенным выше коэффициентам теплопроводности и вязкости. Они имеют вид:
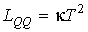 , , | (2.96) |
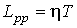 . . | (2.97) |
Тогда выражения для термодинамических сил примут форму:
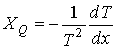 , , | (2.98) |
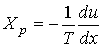 , , | (2.99) |
а соответствующие формулы для расчета производства энтропии принимают вид
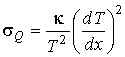 , , | (2.100) |
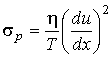 . . | (2.101) |
Анализ полученных выражений показывает, что при протекании необратимых процессов теплопроводности и вязкости производство энтропии является положительной величиной. Если газ находится в равновесном состоянии, которое характеризуется постоянством параметров состояния (в данном случае, если 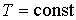 и 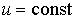 ), то в такой среде будут отсутствовать термодинамические потоки и производство энтропии станет равным нулю.
Задача 2.7. Определить производство энтропии в газе, находящимся между двумя плоскими стенками, имеющими температуры 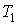 и 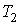 . Считать, что расстояние между стенками 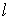 много меньше линейных размеров стенок.
Решение: Так как, если пренебречь краевыми эффектами, плотность потока теплоты во всех точках газа между близко расположенными друг к другу стенками должна быть одинаковой, то в установившемся режиме можно записать:
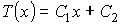 ,
где константы 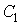 и 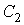 могут быть определены из граничных условий 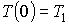 и 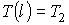 . Тогда имеем:
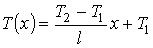 ,
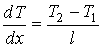 .
Подстановка этих выражений в формулу (2.100) дает
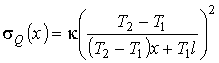 .
Из полученного выражения следует, что в разных точках газа производство энтропии различно.
Производство энтропии внутри всего газа, расположенного между стенками, можно вычислить с помощью формулы (2.92):
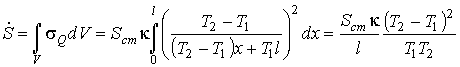 ,
где 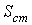 - площадь поверхности стенки.
Такой же результат можно получить и воспользовавшись для определения производства энтропии непосредственно выражением (1.45):
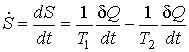 ,
где 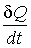 - поток теплоты 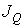 , взятый с обратным знаком:
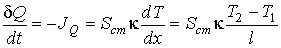 .
Подстановка этого выражения в предыдущую формулу позволяет получить следующее выражение
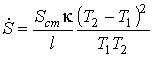 ,
которое полностью совпадает с формулой, полученной выше первым способом.
|