2.4. Принцип Ле-Шателье - Брауна
Общее условие устойчивости равновесия изолированных систем может быть сформулировано на основе закона возрастания энтропии. Из этого закона следует, что возрастание энтропии изолированной системы происходит до тех пор, пока в ней не затухают все необратимые процессы. В этом случае энтропия достигает максимального значения. Следовательно, условие устойчивости состояния термодинамической системы можно сформулировать следующим образом:
Данное условие означает, что при устойчивом термодинамическом равновесии энтропия 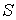 адиабатически изолированной системы имеет экстремум: 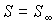 , где 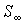 - энтропия системы в состоянии термодинамического равновесия. Следовательно, в состоянии устойчивого равновесия первая вариация энтропии 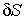 изолированной термодинамической системы равна нулю: 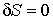 , а вторая ее вариация 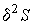 – меньше нуля: 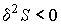 . В данном случае под вариацией энтропии понимается ее бесконечно малое изменение при бесконечно малом изменении параметров состояния, которые приводят к переводу системы в неравновесное состояние. Условие равенства нулю первой вариации энтропии 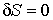 дает необходимое условие равновесия изолированной системы, а неравенство 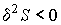 - достаточное условие устойчивости равновесного состояния.
На термодинамическую систему, находящуюся в состоянии устойчивого равновесия, могут воздействовать внешние факторы, выводящие ее из этого состояния. Реакцию системы на эти воздействия можно качественно определить на основе принципа Ле-Шателье - Брауна:
Противодействие внешним воздействиям протекающими в системе процессами напоминает известное в электродинамике правило Ленца.
Сформулированный принцип позволяет предсказать направление протекания процессов в термодинамической системе, которая выводится из состояния устойчивого равновесия внешними воздействиями.
Задача 2.6. Один моль идеального газа находится в эластичной оболочке, с внешней стороны которой действует постоянное давление. Показать, что при подводе к этому газу некоторого количества теплоты 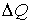 произойдет его расширение, приводящее, в соответствии с принципом Ле-Шателье – Брауна, к уменьшению изменения его температуры 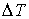 по сравнению с изменением температуры 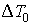 , которое имело бы место при неизменном объеме газа: 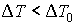 . Проанализировать случай, когда в этой оболочке находится фотонный газ.
Решение: Для одного моля идеального газа в случае изобарического процесса изменение температуры может быть вычислено по формуле
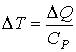 ,
а для изохорического - соответственно определяется выражением
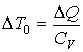 .
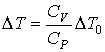 .
Так как 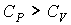 , то 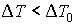 . Из этого следует, что в рассматриваемой термодинамической системе при внешнем воздействии (подводе теплоты) возникает процесс (расширение газа), приводящий к уменьшению влияния внешнего возмущения: изменение температуры газа меньше, чем, если бы расширение не возникало.
Если в оболочке находится фотонный газ, уравнение состояния которого имеет вид: 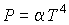 , то при подводе теплоты в изобарическом процессе при 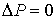 , изменение температуры не происходит: 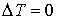 . А для изохорического процесса, учитывая выражение для внутренней энергии фотонного газа: 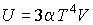 , можно записать
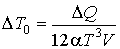 ,
где изменение температуры 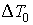 считается малым, по сравнению с температурой газа 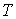 : 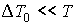 .
Таким образом, происходящие в системе процессы могут не только уменьшить влияние внешнего воздействия, но и скомпенсировать его полностью. Из рассмотренного примера фотонного газа в эластичной оболочке следует, что для такой термодинамической системы подвод теплоты не приводит к увеличению её температуры.
|