2.3. Применение термодинамических потенциалов для описания эффекта Джоуля-Томсона
Адиабатическое расширение газа обычно приводит к изменению его температуры. Если при адиабатическом расширении уменьшение внутренней энергии газа равно совершенной им механической работе над внешними телами, то такой процесс будет обратимым. При обратимом адиабатическом расширении температура газа изменяется в соответствии с уравнением адиабаты. Для идеального газа эта зависимость имеет вид:
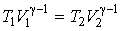 , , | (2.54) |
где: 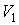 и 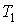 - объем и температура газа в начале процесса, 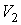 и 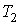 - объем и температура газа после расширения. Так как 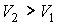 , то из формулы (2.54) следует, что при обратимом адиабатическом расширении идеального газа происходит уменьшение его температуры: 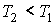 .
Указанное уменьшение температуры идеального газа при его адиабатическом расширении происходит только в том случае, если этот процесс является обратимым. При необратимом адиабатическом расширении идеального газа без совершения им работы над внешними телами его внутренняя энергия и температура остаются неизменными. Поэтому при таком расширении использование выражения (2.54) для определения температуры идеального газа становится невозможным.
При необратимом адиабатическом расширении величина и знак изменения температуры зависят от свойств использующегося в процессе газа. Необратимое адиабатическое расширение газа может быть осуществлено путем его пропускания через пористую перегородку, которая обеспечивает медленное течение газа без возникновения в нем турбулентных потоков, что позволяет считать кинетическую энергию газа малой величиной. Наблюдаемый при этом эффект, заключающийся в изменении температуры газа, называется эффектом Джоуля-Томсона. На примере описания этого эффекта рассмотрим применение метода термодинамических потенциалов.
На рис. 2.1 схематически изображен опыт Джоуля-Томсона. Внутри теплоизолированной трубки помешалась пористая перегородка, через которую осуществлялось медленное стационарное течение газа. Газ внутри пористой перегородки находится в неравновесном состоянии, а процесс его протекания – является необратимым. Но вследствие медленности течения, газ по обе стороны от перегородки можно считать находящимся в равновесии. Давления 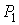 и 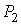 в обеих частях цилиндрической трубки поддерживались постоянными. Пусть при протекании через пористую перегородку некоторой порции газа, имевшей объем 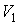 и температуру 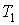 , она приобрела объем 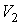 и температуру 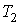 (см. рис. 2.1). | Рис. 2.1.
Схема опыта Джоуля-Томсона |
Проведем описание процесса протекания газа через пористую перегородку. Считая этот процесс достаточно медленным и адиабатическим, а также, учитывая постоянство давлений 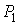 и 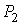 , применим первое начало термодинамики:
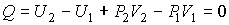 | (2.55) |
или учитывая определение энтальпии (2.28)
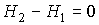 . . | (2.56) |
Следовательно, рассматриваемый процесс является не только адиабатическим, но и изоэнтальпийным.
Далее будем считать, что изменения давления 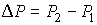 и температуры 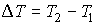 газа в рассматриваемом процессе малы. Тогда с точностью до величин второго порядка малости можно записать:
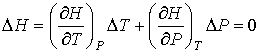 . . | (2.57) |
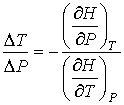 . . | (2.58) |
Для определения частных производных энтальпии 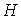 найдем полный дифференциал от выражения (2.28)
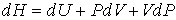 . . | (2.59) |
Тогда с учетом формулы (2.57) имеем:
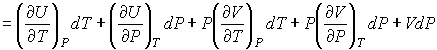 . . | (2.60) |
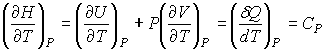 , , | (2.61) |
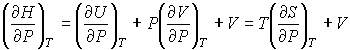 . . | (2.62) |
где 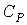 - молярная теплоемкость газа при постоянном давлении. При получении выражения (2.61) использована формула (1.3) с учетом выражения (1.10), а при получении формулы (2.62) – уравнение (2.24).
Дифференцирование выражения (2.43) по давлению 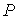 , а формулы (2.44) по температуре 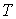 , с учетом равенства перекрестных производных потенциала Гиббса
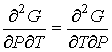 | (2.63) |
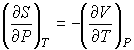 . . | (2.64) |
Подстановка выражения (2.64) в формулу (2.62) и далее, с ее учетом, формул (2.61) и (2.62), в выражение (2.58) позволяет получить следующее соотношение:
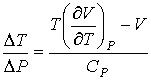 | (2.65) |
или для бесконечно малого изменения давления
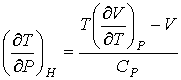 , , | (2.66) |
где производная 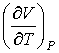 определяется уравнением состояния газа. Формула (2.65) позволяет рассчитать изменение температуры газа при просачивании его через пористую перегородку.
Если при проведении опыта использовать идеальный газ, описываемый уравнением Клапейрона-Менделеева (1.57), то имеем:
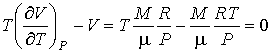 . . | (2.67) |
Следовательно, для идеального газа 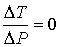 и изменения его температуры при прохождении через пористую перегородку не происходит.
Таким образом, при необратимом адиабатическом расширении идеального газа через пористую перегородку его температура не изменяется, в отличие от обратимого адиабатического расширения, приводящего в соответствии с формулой (2.54) к охлаждению идеального газа.
Данный результат связан с тем, что при адиабатическом расширении идеального газа в опыте Джоуля-Томсона механическая работа не совершается, в отличие от обратимого адиабатического расширения. При применении в этом опыте реального газа совершаемая им механическая работа определяется силами межмолекулярного взаимодействия, и её знак зависит от этих сил.
Рассмотрим применение в опыте Джоуля-Томсона газа Ван-дер-Ваальса, уравнение для одного моля которого имеет вид:
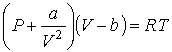 . . | (2.68) |
Раскроем скобки в этом уравнении
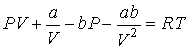 | (2.69) |
и пренебрегая третьим и четвертым слагаемыми в левой части получившегося выражения в связи с их малостью (считая 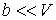 ), продифференцируем его по температуре 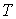 при постоянном давлении 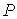 :
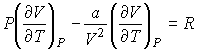 | (2.70) |
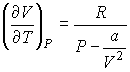 . . | (2.71) |
Выражая 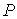 из формулы (2.68) и подставляя в (2.71) с последующим пренебрежением малыми слагаемыми имеем:
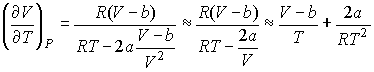 . . | (2.72) |
Тогда формула (2.65) для отношения 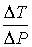 принимает вид
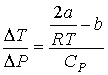 . . | (2.73) |
Из этой формулы следует, что существует температура 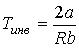 , при которой газ Ван-дер-Ваальса, проходя через пористую перегородку, не изменяет свою температуру. Эта температура 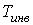 называется температурой инверсии, так как при  отношение 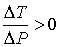 и наблюдается охлаждение газа (так как 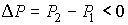 и, следовательно 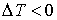 ), а при 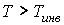 отношение  и газ нагревается. В первом случае эффект Джоуля-Томсона считается положительным, а во втором – соответственно отрицательным.
Процесс охлаждения газа может быть реализован так же с помощью обратимого адиабатического расширения. При таком расширении процесс будет происходить при постоянной энтропии, то есть этот процесс будет изоэнтропийным. Тогда для обратимого адиабатического расширения газа можно на основании формулы (2.29) записать:
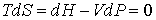 . . | (2.74) |
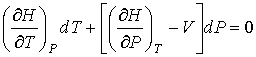 . . | (2.75) |
Отсюда следует, что при описании обратимого адиабатического процесса вместо формулы (2.58) необходимо использовать выражение
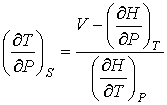 . . | (2.76) |
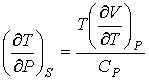 . . | (2.77) |
Для газов характерно изобарическое расширение при их нагревании. Поэтому из условия
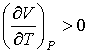 , , | (2.78) |
справедливого для всех газов, следует, что
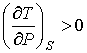 . . | (2.79) |
Поэтому при обратимом адиабатическом расширении газ охлаждается ( 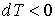 ), так как при этом его давление уменьшается ( 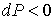 ). В частности, при расширении идеального газа, из формул (2.67) и (2.77) имеем:
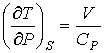 . . | (2.80) |
Для газа Ван-дер-Ваальса при обратимом адиабатическом расширении с учетом формулы (2.72) при условии 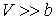 получим следующее выражение для определения изменения его температуры
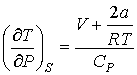 . . | (2.81) |
Из выражений (2.80) и (2.81) следует, что как идеальный газ, так и газ Ван-дер-Ваальса охлаждается при обратимом адиабатическом расширении.
Задача 2.5. Фотонный газ, имеющий температуру 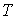 , находится в объеме 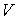 . Величину этого объема резко увеличивают на 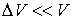 , совершая необратимый адиабатический процесс. Считая, что фотонный газ не совершает при рассматриваемом процессе работы, определить изменение его температуры 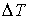 . Решить задачу для случая обратимого адиабатического расширения фотонного газа. Использовать выражения для внутренней энергии 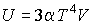 и энтропии 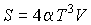 фотонного газа.
Решение: Так как рассматриваемый необратимый адиабатический процесс происходит без теплообмена с окружающей средой: 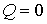 , и, в соответствии с условием задачи, считается, что при его протекании работа не совершается: 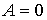 , то из первого начала термодинамики следует сохранение внутренней энергии фотонного газа: 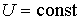 . Тогда имеем:
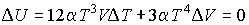 .
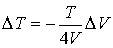 .
В случае обратимого адиабатического процесса должна сохранятся энтропия фотонного газа: 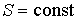 . Поэтому
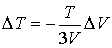 .
Как следует из полученных результатов, охлаждение фотонного газа зависит от того, какой адиабатический процесс (обратимый или необратимый) над ним осуществляется. При этом обратимое адиабатическое расширение фотонного газа обеспечивает его более интенсивное охлаждение, чем необратимое.
|