2.2. Термодинамические потенциалы
Описание равновесных термодинамических процессов может быть выполнено с помощью метода термодинамических потенциалов, разработанного в 1873 - 78 годах американским физиком-теоретиком Гиббсом. Метод термодинамических потенциалов основывается на возможности введения для равновесных процессов функций состояния, полные дифференциалы которых описывают изменение состояния термодинамической системы.
Основное уравнение термодинамики равновесных процессов (2.4)
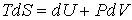 , , | (2.20) |
совместно с уравнением состояния
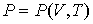 | (2.21) |
и выражением для внутренней энергии
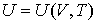 | (2.22) |
образуют систему из трех уравнений, связывающую между собой пять функций состояния: 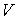 , 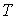 , 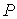 , 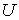 и 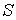 . Если в качестве независимых параметров выбрать объем 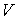 и температуру 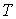 , то система уравнений (2.20) - (2.22) оказывается полностью разрешимой и позволяет определить давление 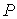 , внутреннюю энергию  и энтропию 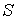 .
В зависимости от выбора двух независимых параметров можно ввести термодинамические потенциалы, дифференцирование которых дает возможность определить другие, неизвестные параметры состояния. При этом используются формулы, которые по своей структуре аналогичны выражению из механики, связывающему потенциальную энергию и консервативную силу.
В зависимости от того, какие параметры состояния термодинамической системы приняты как независимые переменные, можно ввести следующие термодинамические потенциалы.
1. Возьмем в качестве независимых параметров состояния объем 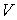 и энтропию 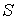 и запишем через эти переменные выражение для внутренней энергии
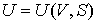 . . | (2.23) |
Тогда уравнение (2.20) можно представить в виде:
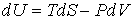 . . | (2.24) |
Учитывая правило нахождения полного дифференциала (см. например, формулы (2.6) и (2.7)), имеем
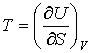 , , | (2.25) |
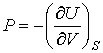 . . | (2.26) |
Как видно эти формулы аналогичны выражениям для нахождения сил в механике через потенциальную энергию консервативной механической системы.
Таким образом, внутренняя энергия, выраженная через параметры состояния 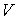 и 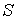 , является термодинамическим потенциалом.
Использование в качестве независимых параметров 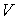 и 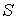 не очень удобно, так как величина энтропии 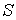 не может быть определена путем непосредственных измерений. Внутренняя энергия 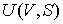 при практических расчетах обычно используется только в случаях, если система является адиабатически изолированной ( 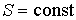 ) или процесс происходит без совершения работы, что имеет место при постоянном объеме системы ( 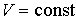 ).
2. Рассмотрим случай, когда независимыми параметрами состояния являются давление 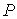 и энтропия 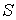 . Преобразуем уравнение (2.20) к виду
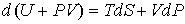 . . | (2.27) |
Введение функции состояния
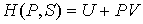 , , | (2.28) |
позволяет представить уравнение (2.27) в форме
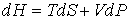 . . | (2.29) |
С учетом правила нахождения полного дифференциала 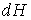 имеем
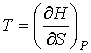 , , | (2.30) |
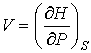 . . | (2.31) |
Функция 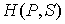 является термодинамическим потенциалом при независимых параметрах 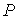 и 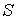 , и называется энтальпией.
Если процесс происходит при постоянном давлении ( 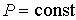 ), то, учитывая формулу 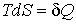 , из выражения (2.29) имеем
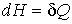 . . | (2.32) |
Следовательно, приращение энтальпии при изобарическом процессе равно количеству теплоты, полученной системой. Энтальпию удобно применять для описания адиабатически изолированных систем, находящихся при постоянном давлении, так как для систем, на которые действуют только механические силы, этот термодинамический потенциал не изменяется.
3. Если в качестве независимых параметров выбрать объем 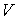 и температуру 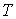 , и уравнение (2.20) представить в виде
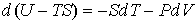 , , | (2.33) |
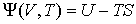 | (2.34) |
будет термодинамическим потенциалом.
Действительно, применяя правило нахождения полного дифференциала для выражения
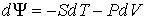 , , | (2.35) |
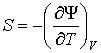 , , | (2.36) |
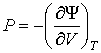 . . | (2.37) |
При изотермическом процессе ( 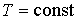 ) с учетом выражения для работы 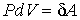 , формула (2.35) дает
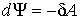 . . | (2.38) |
Из этого выражения следует, что при изотермическом процессе свободная энергия является функцией состояния, уменьшение которой равно работе, совершенной системой. При изотермическом процессе свободная энергия изменяется таким же образом, как внутренняя при адиабатическом процессе.
При описании необратимого процесса, для которого вместо выражения (2.20) необходимо применять неравенство
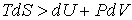 , , | (2.39) |
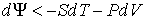 . . | (2.40) |
Если в системе происходит необратимый процесс, при котором температура и давление остаются постоянными, то для такого процесса 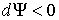 , а для обратимого – соответственно 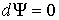 . Это означает, что при необратимом процессе свободная энергия уменьшается, и достигает своего минимума при достижении термодинамической системой состояния равновесия. Условие минимума свободной энергии для состояний, при которых 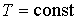 и 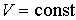 , применяется при определении параметров, характеризующих равновесное состояние термодинамической системы.
4. При выборе в качестве независимых переменных давления 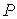 и температуры 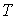 и введения функции состояния в форме
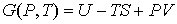 , , | (2.41) |
уравнение (2.27) может быть преобразовано к виду
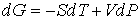 . . | (2.42) |
Так как 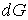 является полным дифференциалом, то имеем:
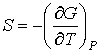 , , | (2.43) |
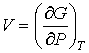 . . | (2.44) |
При описании необратимого процесса на основании формулы (2.39) имеем
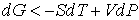 . . | (2.45) |
Из этого выражения следует, что для необратимого процесса, происходящего при постоянных значениях температуры и давления, потенциал Гиббса уменьшается: 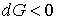 . После достижения системой состояния равновесия потенциал Гиббса принимает минимальное значение и становится постоянной величиной: 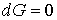 (см. формулу (2.42)). Это позволяет использовать условие минимума потенциала Гиббса для описания равновесных состояний, при которых 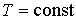 и 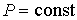 .
Между термодинамическими потенциалами могут быть установлены соотношения, позволяющие выразить одни потенциалы через другие. Подстановка выражения (2.36) в формулу (2.34) дает уравнение Гиббса-Гельмгольца:
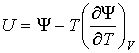 , , | (2.46) |
связывающие между собой внутреннюю энергию 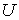 и свободную энергию 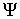 .
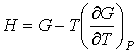 , , | (2.47) |
устанавливающие взаимосвязь энтальпии 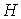 и потенциала Гиббса 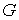 .
Для термодинамической системы, состоящей из 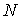 одинаковых частиц, с помощью потенциала Гиббса можно ввести термодинамический потенциал, рассчитанный на одну частицу:
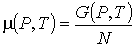 . . | (2.48) |
Этот термодинамический потенциал называется химическим потенциалом. При получении формулы (2.48) сделано предположение, что давление и температура остаются неизменными при изменении числа частиц в термодинамической системе.
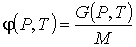 , , | (2.49) |
где 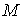 - масса вещества в системе.
Сопоставление формул (2.48) и (2.49) позволяет записать соотношение между химическим и удельным термодинамическим потенциалами
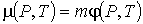 , , | (2.50) |
где 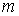 - масса одной частицы вещества.
Деление выражения (2.42) на массу 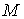 позволяет записать его для удельного термодинамического потенциала
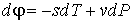 . . | (2.51) |
Здесь введены обозначения для удельной энтропии: 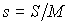 и удельного объема: 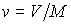 .
Выражения для значений удельных энтропии 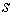 и объема 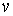 через удельный термодинамический потенциал 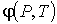 имеют вид, аналогичный формулам (2.43) и (2.44)
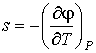 , , | (2.52) |
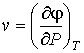 . . | (2.53) |
Удельный термодинамический потенциал (химический потенциал) применяется для описания термодинамических систем с переменным числом частиц. Примером такой системы является система, в которой происходит фазовый переход вещества из одного агрегатного состояния в другое. В третьей главе нами проведено описание фазовых переходов, при котором использованы свойства удельного термодинамического потенциала.
Задача 2.3. Определить выражения для внутренней энергии 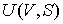 одного моля идеального газа. Записать аналогичное выражение для одного моля газа Ван-дер-Ваальса.
Решение: На основании формулы (2.19) можно записать зависимость температуры для одного моля идеального газа от его объема и энтропии
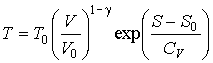 ,
где учтено соотношение 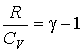 , 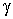 - показатель адиабаты.
Тогда подстановка этой зависимости в формулу (2.17) при 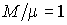 дает выражение для внутренней энергии одного моля идеального газа
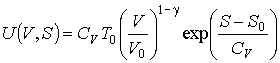 .
Выполнение аналогичных преобразований для случая одного моля газа Ван-дер-Ваальса позволяет получать следующее выражение
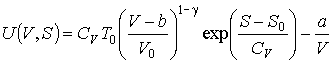 .
При выводе этой формулы использованы полученные в задаче 2.1 выражения для внутренней энергии и энтропии газа Ван-дер-Ваальса.
Задача 2.4. Определить термодинамические потенциалы фотонного газа, если известны уравнение его состояния 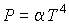 , выражения для внутренней энергии 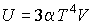 и энтропии 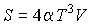 .
Решение: Использование приведенных в условии задачи выражений для внутренней энергии 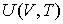 и энтропии 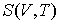 позволяет получить зависимость внутренней энергии 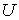 от параметров 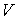 и 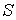 :
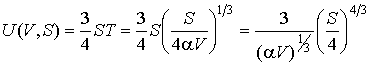 .
Аналогично найдем другие термодинамические потенциалы:
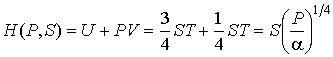 ;
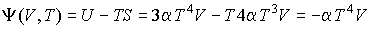 ,
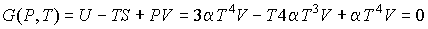 .
Равенство нулю потенциала Гиббса для фотонного газа делает невозможным использование этого потенциала при расчетах и связано с тем, что переменные 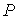 и 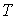 для этого газа не являются независимыми, а связаны между собой однозначным соотношением 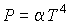 .
|