1.5. Термодинамическая энтропия
Понятие термодинамической энтропии, впервые введенное в 1865 году Клаузиусом, имеет ключевое значение для понимания основных положений термодинамики.
Рассмотрим обратимый круговой термодинамический процесс, представленный на рис. 1.5. Для этого процесса может быть записано равенство Клаузиуса (1.42) в виде
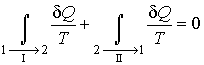 , , | (1.43) |
где первый интеграл берется по траектории 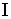 , а второй - соответственно по траектории  . | Рис. 1.5.
Обратимый круговой термодинамический процесс |
Изменение направления протекания процесса 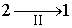 на противоположное 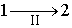 , что можно выполнить вследствие обратимости процесса  , приводит к замене знака перед вторым интегралом формулы (1.43). Выполнение этой замены и перенос второго интеграла в выражении (1.43) в правую часть дают
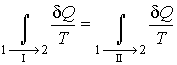 . . | (1.44) |
Из полученного выражения следует, что для обратимых процессов интеграл 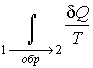 не зависит от конкретного вида траектории, по которой происходит процесс, а определяется только начальным и конечным равновесными состояниями термодинамической системы.
Элементарное приведенное количество теплоты 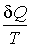 представляет собой полный дифференциал некоторой функции 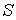 , зависящей только от состояния термодинамической системы, то есть:
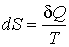 . . | (1.45) |
Тогда интеграл 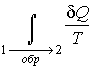 будет равен разности значений функции 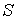 в равновесных состояниях 1 и 2:
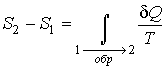 . . | (1.46) |
Из выражения (1.46) следует, что термодинамическая энтропия, так же как и потенциальная энергия, определяется с точностью до произвольной постоянной. Это связано с тем, что формула (1.46) не позволяет определить абсолютное значение термодинамической энтропии, а дает только разность энтропий для двух равновесных состояний, как суммарную приведенную теплоту в обратимом термодинамическом процессе, переводящим систему из одного состояния в другое.
Термодинамическая энтропия, введенная выше, применима для описания равновесного состояния термодинамической системы. Для нахождения энтропии 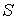 термодинамической системы, находящейся в квазиравновесном состоянии, при котором можно считать, что её отдельные части (подсистемы) находятся в состоянии равновесия, можно воспользоваться свойством аддитивности энтропии:
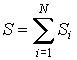 , , | (1.47) |
где: 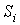 - энтропии подсистем, 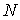 - число подсистем.
Свойство аддитивности энтропии позволяет описывать состояния макроскопической системы, не находящейся в равновесии, путем её разбиения на достаточно большое число подсистем, которые можно считать находящимися в состоянии локального равновесия. Такой подход дает возможность распространить результаты равновесной термодинамики на системы, находящиеся в неравновесном состоянии, но которые можно представить как состоящие из некоторого числа равновесных подсистем.
Применим неравенство Клаузиуса для описания необратимого кругового термодинамического процесса, изображенного на рис 1.6. | Рис. 1.6.
Необратимый круговой термодинамический процесс |
Пусть процесс 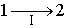 будет необратимым, а процесс 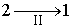 - обратимым. Тогда неравенство Клаузиуса для этого случая примет вид
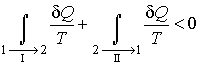 . . | (1.48) |
Так как процесс 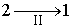 является обратимым, для него можно воспользоваться соотношением (1.46), которое дает
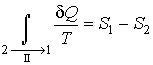 . . | (1.49) |
Подстановка этой формулы в неравенство (1.48) позволяет получить выражение
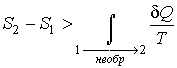 . . | (1.50) |
Сравнение выражений (1.46) и (1.50) позволяет записать следующее неравенство
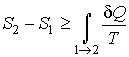 , , | (1.51) |
в котором знак равенства имеет место в случае, если процесс 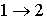 является обратимым, а знак больше, если процесс 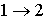 - необратимый.
Неравенство (1.51) может быть также записано и в дифференциальной форме
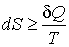 . . | (1.52) |
Если рассмотреть адиабатически изолированную термодинамическую систему, для которой 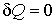 , то выражение (1.52) примет вид
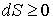 | (1.53) |
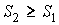 . . | (1.54) |
Записанное утверждение является ещё одной формулировкой второго начала термодинамики.
Таким образом, изолированная термодинамическая система стремится к максимальному значению энтропии, при котором наступает состояние термодинамического равновесия.
Задача 1.4. Термодинамическая система, состоящая из двух находящихся в тепловом контакте тел, помещена в адиабатическую оболочку. Теплоемкости тел одинаковы и равны 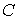 . Температура первого тела в некоторый момент времени равна 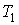 , а второго - 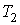 , причем 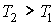 . Найти уравнение, описывающее изменение энтропии системы с течением времени при её стремлении к состоянию термодинамического равновесия. Считать, что передача теплоты от одного тега к другому описывается формулой: 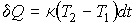 , где 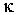 - коэффициент теплопередачи.
Решение: После достижения системой состояния термодинамического равновесия температура тел станет одинаковой:
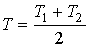 ,
а её энтропия примет максимальное значение 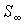 .
Изменение энтропии системы при её переходе в равновесие можно определить по формуле:
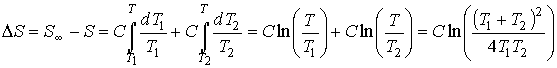 .
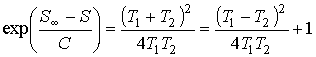 .
В соответствии со свойством аддитивности энтропии и формулой (1.45) для изменения энтропии системы можно записать:
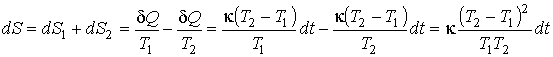 .
Здесь учтено, что теплота отводится от второго тела и подводится к первому.
Тогда уравнение, описывающее изменение энтропии с течением времени при стремлении системы к состоянию термодинамического равновесия, примет окончательный вид:
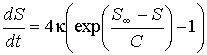 .
При 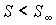 правая часть этого уравнения больше нуля, что соответствует росту энтропии с течением времени: 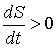 . При достижении энтропией системы 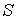 равновесного (максимального) значения 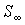 , правая часть полученного уравнения становится равной нулю, и дальнейшего роста энтропии не происходит.
|