1.4. Второе начало термодинамики
Сформулированное выше первое начало термодинамики определяет соотношение между количеством подводимой к телу теплоты, совершаемой при этом механической работой и изменением внутренней энергии тела. При этом первое начало термодинамики не ограничивает возможность протекания термодинамического процесса в любом направлении. В частности, оно допускает как процесс самопроизвольной передачи теплоты от более нагретого тела к менее нагретому, так и обратный процесс самопроизвольного перехода теплоты от холодного тела к горячему. Но из повседневного опыта нам известно, что при соединении двух тел с разными температурами происходит охлаждение горячего и нагрев холодного. Обратный процесс в природе самопроизвольно не наблюдается и для его организации требуется создание специальных холодильных машин, работающих с использованием внешних источников энергии.
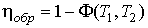 ; ; | (1.31) |
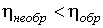 . . | (1.32) |
Сравнение формул для к.п.д. цикла Карно тепловой машины, работающей на идеальном газе (1.30), и приведенной выше формулы (1.31) позволяет записать математическую формулировку первой теоремы Карно в следующем виде:
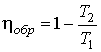 . . | (1.33) |
Возможность применения формулы (1.33) для расчета к.п.д. любой обратимой тепловой машины связана с тем, что вид функции 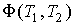 для всех рабочих тел, в том числе и для идеального газа, должен быть одинаков.
Совместное применение первой и второй теорем Карно позволяет получить следующее неравенство:
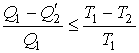 . . | (1.34) |
Знак равенства в этой формуле соответствует случаю описания обратимой тепловой машины, а знак меньше – описанию необратимой тепловой машины.
Формулу (1.34) можно преобразовать в виду
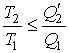 . . | (1.35) |
Выражение (1.35) в свою очередь дает
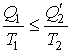 , , | (1.36) |
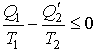 . . | (1.37) |
Если полученное выражение записать через количество теплоты, подводимой к рабочему телу от нагревателя 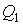 и холодильника 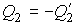 , то оно примет окончательную форму
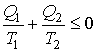 . . | (1.38) |
В общем случае неравенство (1.38) может быть записано в виде
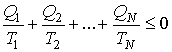 | (1.39) |
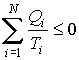 , , | (1.40) |
При переходе к бесконечному числу тепловых резервуаров, с которыми рабочее тело тепловой машины обменивается теплотой, суммирование в формуле (1.40) может быть заменено интегрированием по замкнутому термодинамическому циклу:
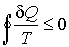 . . | (1.41) |
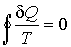 , , | (1.42) |
имеющее принципиальное значение для построения равновесной термодинамики.
Случай строгого неравенства в формуле (1.41) соответствует описанию необратимых круговых термодинамических процессов, и это выражение применяется в неравновесной термодинамике.
|