1.2. Первое начало термодинамики
Таким образом, количество теплоты может быть определено как разность изменения внутренней энергии системы и механической работы, совершённой над системой:
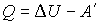 , , | (1.1) |
где 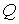 – количество теплоты, переданной системе, 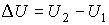 – изменение внутренней энергии системы при её переходе из первого состояния во второе, 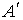 – работа, совершённая над системой.
Так как работа, совершенная над системой 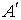 , равна работе, совершенной системой 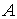 , взятой с обратным знаком: 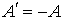 , то первое начало термодинамики может быть сформулировано следующим образом:
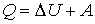 . . | (1.2) |
Если к термодинамической системе подводится элементарное количество теплоты 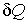 , то оно расходуется на изменение внутренней энергии 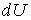 и совершение элементарной работы 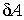 :
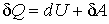 . . | (1.3) |
Отметим принципиальное отличие величины 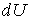 и величин 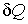 и 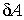 . Величина 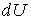 представляет собой полный дифференциал, то есть бесконечно малое изменение величины 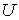 , и поэтому интеграл от неё равен разности внутренних энергий системы в двух состояниях, конечном и начальном:
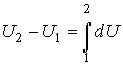 . . | (1.4) |
Интегралы (суммы) от малых величин 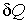 и 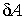 являются количеством теплоты 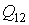 , переданной системе, и работой 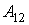 , совершенной системой при ее переходе из первого состояния во второе:
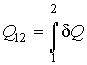 , , | (1.5) |
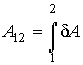 . . | (1.6) |
В отличие от внутренней энергии, являющейся функцией состояния, теплота и работа функциями состояния не являются, а зависят от того, каким образом система переведена из одного состояния в другое.
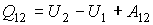 . . | (1.7) |
Эта формула представляет собой запись первого начала термодинамики применительно к случаю перехода термодинамической системы из некоторого первого состояния во второе.
По своему физическому смыслу первое начало термодинамики представляет собой закон сохранения (изменения) энергии в термодинамике. Если, согласно закону изменения энергии в механике, работа неконсервативных сил равна приращению механической энергии системы (в частности, имеющая отрицательный знак работа сил трения равна уменьшению механической энергии системы), то согласно первому началу термодинамики, приращение внутренней энергии термодинамической системы равно сумме работы внешних сил, совершенной над системой, и энергии, переданной системе путём теплопередачи.
В случае, если термодинамические процессы в системе квазиравновесные, и потоки энергии, вещества и т.д. в ней отсутствуют, то можно пренебречь внутренним трением, считая, что изменения объёма и давления определяют изменение состояния системы.
Работа 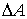 , совершаемая телом (например, газом) над внешними телами при перемещении элемента поверхности этого тела (оболочки газа), площадью  , на расстояние  вдоль нормали к поверхности равна:
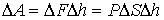 , , | (1.8) |
где: 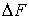 - сила, действующая по нормали к поверхности 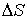 , 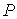 – внешнее давление, которое считается неизменным при перемещении элемента 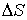 на расстояние 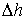 . Если давление 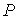 одно и то же во всех точках поверхности тела, то, просуммировав по всей поверхности, получим:
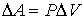 , , | (1.9) |
где 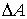 – работа, совершённая телом при приращении его объёма на малую величину 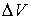 (см. рис. 1.1). | Рис. 1.1.
Иллюстрация к расчету элементарной работы при изменении объема тела |
Для элементарной работы 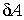 выражение (1.9) принимает вид:
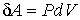 . . | (1.10) |
Работа при конечных изменениях объёма тела может быть определена путем интегрирования выражения (1.10):
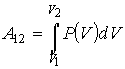 . . | (1.11) |
Этот интеграл зависит от пути перехода из состояния с объемом 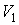 в состояние с объемом 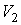 , так как функция 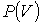 может иметь различный вид.
Рис. 1.2 иллюстрирует зависимость величины интеграла (1.11), численно равного площади под кривой 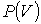 , от вида функции 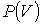 . | Рис. 1.2.
Работа при переходе из одного состояния термодинамической системы в другое |
В зависимости от траектории I или II перехода из первого состояния во второе, площадь под кривой 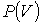 будет различна, а, следовательно, будет различна механическая работа, совершаемая системой в этих термодинамических процессах. Количество теплоты 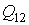 , необходимое для перехода из первого состояния во второе, также будет зависеть от вида кривой 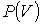 (формы траектории). В этом можно убедится, если учесть тот факт, что внутренняя энергия является функцией состояния термодинамической системы, и ее изменение при переходе из первого состояния во второе не зависит от пути этого перехода. А, следовательно, в соответствии с первым началом термодинамики (см. формулу (1.2)) теплота, также как и работа, должна зависеть от термодинамического процесса, с помощью которого производился переход термодинамической системы.
Задача 1.1. Найти работу, совершаемую газом, при его расширении от объема 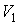 до объема 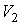 , если зависимость давления 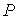 от объема 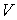 выражается формулой: 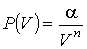 , где 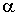 и 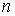 - известные константы.
Решение: В соответствии с формулой (1.11) имеем:
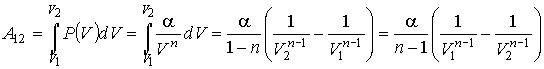 .
|