2.1. Точечные дефекты.
Точечные дефекты - самые мелкие дефекты, обычно связаны с "ненормальной" ситуацией вокруг одного атома (отсутствием одного атома, замещением одного атома другим или же появлением "лишнего" атома). Рассмотрим различные точечные дефекты, схематически изображенные на рис. 2.1.
Вакансия. Атом может отсутствовать в некотором узле кристаллической решетки (см. рис. 2.1 (1)). Такое пустое место называют вакансией. Часто вакансия появляется при кристаллизации - случайно один узел оказывается пустым, и, если следующий слой атомов закрывает подход атомов из раствора или расплава к пустому узлу-вакансии, то узел может оказаться пустым. Вакансию часто называют - дефект по Шотки.
Междоузельный атом. Атом может разместиться не в узле кристаллической решетки, а в промежутке между атомами - междоузлии (см. рис. 2.1 (2)), такой дефект называют междоузельным атомом. Появляется междоузельный атом, как и вакансия, часто при кристаллизации - случайно один из атомов в результате теплового движения попадет в промежуток между соседними атомами, и, если его место займет какой либо другой атом, то междоузельный атом так и останется в новом ненормальном положении.
Дефект по Френкелю. Часто вакансия и межузельный атом возникают парами (см. рис. 2.1 (3)), в этом случае один из атомов перескакивает из узлового положения в соседнее междоузлие. Причиной такого перескока может быть тепловое движение при сравнительно высоких температурах, порядка температуры плавления, или выбивание атома быстродвижущейся частицей (радиационный дефект). Такая пара дефектов называется дефектом по Френкелю.
Атом примеси. Один из атомов может быть замещен атомом примеси (см. рис. 2.1 (4)), при этом также получается дефект, называемый примесным атомом замещения. Примесный атом может разместиться и в междоузлии (см. рис. 2.1 (5)), как бы внедрившись в него. Такой дефект, называемый примесным атомом внедрения, часто появляется в случае, когда атом примеси значительно меньше атомов кристалла и в решетке кристалла имеются междоузлия достаточного размера; часто примесями внедрения оказываются атомы водорода, бора, углерода. Если атом примеси превосходит по размерам атомы кристалла, то, как правило, он замещает атомы кристалла.
| Рис. 2.1.
Типы точечных дефектов: 1 - вакансия; 2 - межузельный атом; 3 - дефект по Френкелю; 4 - примесный атом замещения; 5 - примесный атом внедрения; 6 - атом замещения большей валентности |
Часто атомы примеси, отличающиеся валентностью от атомов кристалла, обусловливают появление вакансий, как это происходит в кристаллах 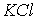 при добавлении к нему 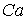 , так, что кристалл в целом остается нейтральным. В таком случае атом двухвалентного кальция занимает место одного атома калия, а место, где должен был бы находиться атом калия, оказывается пустым (см. рис. 2.1 (6)).
Энергия точечного дефекта и вероятность его образования. С точечным дефектом связана энергия 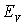 образования дефекта: в случае вакансии ( это энергия, необходимая для удаления атома на поверхность кристалла; в случае внедренного атома - энергия необходимая для перемещения атома с поверхности кристалла в междоузлие. Как правило, она составляет примерно 1 эВ. Вероятность образования точечного дефекта вычисляется по формуле Больцмана:
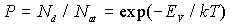 | (2.1) |
Вероятность 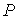 , вычисленная по этой формуле (см. задачу 2.1) при 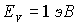 и 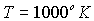 , окажется равной 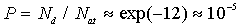 . При более низких температурах плотность дефектов убывает экспоненциально и оказывается очень малой величиной при температурах ниже комнатной. Однако и при низких температурах плотность дефектов может оказаться высокой, если кристалл, нагретый до высокой температуры, быстро охладить (закалить). Тогда плотность дефектов будет соответствовать высокой температуре.
В случае дефекта по Френкелю, для образования пары дефектов (вакансии и межузельного атома) потребуется энергия 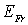 , численно равная энергии необходимой для удаления атома на поверхность кристалла, а затем для перемещения атома с поверхности кристалла в междоузлие. Можно показать, что число таких дефектов вычисляется по формуле:
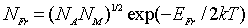 | (2.2) |
где 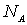 и 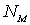 соответственно число узлов и междоузлий в кристалле.
С повышением температуры равновесное количество дефектов возрастает, и на их образование требуется дополнительная энергия. Поэтому в некоторых кристаллах вблизи температуры плавления, когда при нагреве намного увеличивается число дефектов, наблюдается эффект увеличения теплоемкости, сопоставимый с типичными значениями молярной теплоемкости, связанной с колебаниями кристаллической решетки (см. рис. 2.2). | Рис. 2.2.
Вклад в теплоемкость, связанный с образованием точечных дефектов вблизи температуры плавления |
Влияние точечных дефектов на диффузию. Точечные дефекты оказывают наиболее значительное влияние на скорость диффузии в кристаллах и на электропроводность в диэлектрических кристаллах. Остановимся, прежде всего, на возможных механизмах диффузии в кристаллах.
Атомы в кристаллах могут перескакивать из одного положения в другое. Возможные варианты таких перескоков изображены на рис. 2.3. Два или четыре атома могут поменяться местами (см. рис. 2.3 (1, 2)). Однако атому гораздо легче (это показывают как наглядные соображения о том, как "легче протиснуться атому между другими, раздвигая их", так и строгие расчеты) перескакивать в вакансию (см. рис. 2.3 (3)). Также сравнительно легко перескакивать межузельному атому, особенно если он небольшого размера (см. рис. 2.3 (4)). Поэтому основными механизмами диффузии в твердых телах считают вакансионный, связанный с перегруппировками атомов вблизи вакансий (см. рис. 2.3 (3)) и межузельный, связанный с перемещениями, как правило, сравнительно мелких атомов по междоузлиям (см. рис. 2.3 (4)). | Рис. 2.3.
Наиболее распространенные механизмы диффузии атомов в кристаллах: 1 - обмен местами двух соседних атомов; 2 - обмен местами нескольких соседних атомов; 3 - перескок атома в вакансию; 4 - перескоки межузельных атомов в соседние междоузлия |
Во всех случаях диффузии атомы должны преодолевать потенциальный барьер; происхождение которого связано главным образом с квантовыми силами отталкивания, сильно увеличивающимися при сближении атомов. Рассмотрим наиболее простой для анализа случай перескакивания межузельного атома в соседнее междоузлие. На рис. 2.4 схематически изображена зависимость энергии межузельного атома от координаты 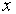 . Энергия, необходимая для такого перескока, называется энергией активации 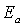 . Она обычно значительно больше средней энергии теплового движения ( 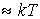 ). Вероятность такого события очень мала и задается формулой Больцмана:
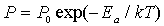 . . | (2.3) |
Поэтому атомы в кристаллах в течение длительного времени испытывают колебания около положения равновесия с некоторой частотой 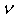 , и только очень редко, когда случайно энергия тепловых колебаний превысит энергию активации, могут перепрыгнуть на новое место. Можно приблизительно оценить частоту 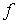 таких перескоков как:
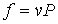 . . | (2.4) |
| Рис. 2.4. Зависимость энергии межузельного атома от координаты 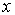 . Энергия атома минимальна в междоузлиях и максимальна в положениях А. |
Таким образом, атом в твердых телах перемещается редкими прыжками, на расстояние 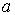 и частотой 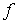 как это схематически показано на рис 2.5. | Рис. 2.5.
Схематическое изображение процесса диффузии межузельных атомов в примитивной кубической решетке |
С помощью такой модели движения атомов рассчитаем коэффициент диффузии межузельных атомов в случае простой кубической решетки с параметром 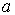 . Пусть частота перескоков из данного междоузлия в соседнее равна 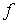 .
Вспомним закон диффузии Фика, связывающий поток числа атомов 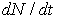 через площадку 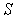 и градиент концентрации 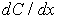 :
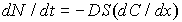 | (2.5) |
Параметр 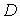 называется коэффициентом диффузии. Он зависит от типа диффундирующего атома и вещества, в котором происходит диффузия заданных атомов. Рассмотрим в кристалле направление [100] и перпендикулярную ему плоскость 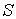 , и проходящую через узлы решетки (отмечены кружочками на рис. 2.6 а). Также рассмотрим две параллельные соседние плоскости 1 и 2, проходящие соответственно слева и справа через ближайшие к выбранной плоскости междоузлия (обозначены квадратиками). Расстояние между плоскостями 1 и 2, равное расстоянию между междоузлиями, равно также параметру решетки и "длине перескока" 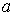 . Пусть на участке площади 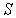 плоскости 1 находится 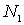 межузельных атомов, а на таком же по площади участке плоскости 2 - 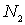 межузельных атомов (см. рис. 2.6 а).
Можно рассчитать входящие в закон диффузии концентрации 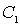 и 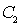 межузельных атомов в точке с координатой 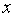 и 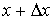 . Очевидно:
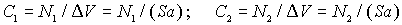 . . | (2.6) |
| Рис. 2.6.
Расположение узлов и междоузлий кубической примитивной решетке (а) Расположение междоузлий ближайших к заданному (б) в этой решетке |
Вычислим число атомов 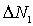 , пересекших за 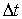 плоскость 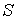 слева направо. Каждый атом первой плоскости может перепрыгнуть в одно из шести ближайших мест (см. рис. 2.6 б), только одно из них соответствует пересечению атомом выбранной центральной плоскости. Тогда
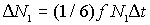 . . | (2.7) |
Аналогично вычисляется число атомов 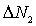 , пересекших за 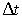 выбранную плоскость 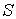 справа налево:
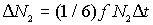 . . | (2.8) |
Общее число атомов, пересекших плоскость, окажется равным:
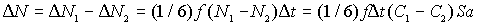 | (2.9) |
С учетом, что 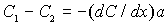 , получаем:
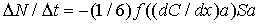 | (2.10) |
Сравнивая (2.10) и (2.5), получим, что коэффициент диффузии оказывается равным:
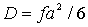 . . | (2.11) |
Примерно по такой же схеме можно рассчитать коэффициенты диффузии и в других изображенных на рис. 2.3 случаях, характерная энергия активации будет другой, причем в случаях 1 и 2 она будет больше, чем в случаях 3 и 4. Заметим, что энергия активации при перегруппировке атомов вблизи вакансии будет значительно меньше, чем в случаях 1 и 2. Несмотря на то, что число вакансий в соответствии с (2.1) обычно небольшое, вклад в диффузию по механизму 3 значительно превосходит вклад в диффузию по механизму 1 и 2 из-за меньшей энергии активации и, следовательно, большей вероятности перескока атомов.
Общим для всех случаев диффузии, изображенных на рис. 2.3, окажется экспоненциальная зависимость коэффициента диффузии от температуры вида:
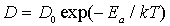 | (2.12) |
Параметры 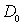 и 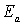 этой формулы измерены экспериментально для каждой пары диффундирующий элемент - вещество, в котором происходит диффузия (см. табл. 2.1).
Параметры 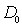 и 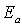 формулы (2.12) для некоторых пар диффундирующий элемент - вещество.
Элементы | 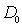 , м 2/с | 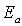 , эВ |
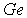 в 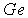 | | 3,0 |
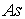 в 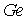 | | 2,5 |
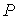 в 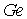 | | 2,5 |
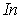 в 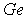 | | 2,5 |
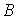 в 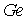 | | 4,5 |
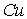 в 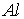 | | 1,45 |
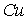 в 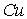 | | 2,05 |
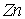 в 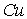 | | 1,98 |
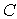 в 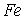 (ОЦК-железо) | | 0,9 |
 в  | | 1,20 |
На рис. 2.7 изображена зависимость коэффициента диффузии углерода в ОЦК железе от температуры. Видно, что соотношение (2.12) выполняется весьма точно. | Рис. 2.7.
Зависимость коэффициента диффузии углерода в ОЦК железе от температуры |
С помощью рассмотренной выше модели диффузии можно оценить среднее смещение 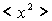 атома в кристалле за время 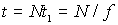 (здесь 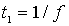 ( среднее время между последовательными перескоками атома). Для этого вычисляют величину 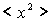 в предположении о полной независимости последующих прыжков друг от друга [2]. В этом случае можно получить формулу:
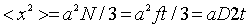 | (2.13) |
Эта формула используется для экспериментального определения величины 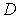 .
Диффузию в твердых телах в настоящее время наиболее эффективно изучают с использованием "меченых атомов". Для таких исследований на поверхность вещества наносят определенное количество радиоактивных меченых атомов. Затем образец выдерживается при заданной температуре в течение времени достаточного для диффузии "меченых атомов" на глубину порядка 0,3-1 мм. Затем измеряется активность образца. После удаления шлифованием слоя вещества заданной толщины снова измеряется активность образца, и так несколько раз. Таким образом можно определить среднюю глубину проникновения "меченых атомов" в вещество и вычислить коэффициент диффузии 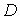 при заданной температуре. Проделав серию опытов при различных температурах можно определить параметры 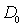 и 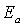 формулы (2.12).
Можно по формулам (2.3) и (2.4) и данным табл. 1.1 получить оценки частот перескоков атомов при различных температурах. Так атом углерода в альфа-железе при температуре 1800 К перескакивает 10 11 раз в секунду, при комнатной температуре - 1 раз за десятки секунд. Таким образом, заметную роль диффузия играет только при высоких температурах, сопоставимых с температурой плавления вещества. Известно, что защитное никелевое или хромовое покрытие железа при комнатной температуре практически не "впитывается" в железо, а при температуре 1000-1300 К этот процесс сильно ускоряется. Кратковременные нагревы для легирования полупроводника примесями используются в полупроводниковой технике изготовления интегральных схем: нанесенные напылением на нужные участки поверхности полупроводникового кристалла легирующие примеси при нагреве на несколько сотен градусов диффундируют в полупроводник и легируют его, образуя в кристалле сложную систему областей полупроводников 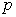 - и 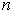 - типа.
Диффузия, происходящая главным образом за счет перемещения дефектов, является механизмом постепенного изменения числа дефектов в веществе. Известно (см. формулу (2.1)), что вероятность образования дефекта при температуре, значительно меньшей температуры плавления вещества, очень мала. Однако обычно число дефектов во много раз больше, так как дефекты зарождались при высоких температурах: либо во время роста кристаллов, либо после закалки от высокой температуры. Постепенно плотность дефектов уменьшается. Происходит это благодаря либо попаданию межузельных атомов в вакансию (рекомбинация дефектов, подобная рекомбинации электронов и дырок в полупроводниках), либо благодаря перемещению дефекта на поверхность кристалла или границы кристаллического зерна. В некоторых случаях (см. разд. 2.3) точечные дефекты - примесные атомы группируются, образуя выделения новой фазы. Перечисленные процессы называют залечиванием дефектов.
Часто проводят специальные термообработки, состоящие в длительных выдержках детали при постепенно понижающейся температуре, имеющие целью ускорить залечивание дефектов. После такой термообработки количество дефектов меньше меняется впоследствии, а значит, меньше изменяются и свойства материала в процессе его эксплуатации. По таким схемам обрабатывают, например, калиброванные электросопротивления точных приборов, постоянные магниты и т. п.
Влияние точечных дефектов на электропроводность. Электропроводность реальных кристаллов оказывается значительно выше электропроводности идеального кристалла-диэлектрика, вычисленной в рамках зонной теории. Это связано с двумя главными причинами.
Во-первых, с наличием донорных или акцепторных примесей, которые увеличивают проводимость диэлектрика по тем же механизмам что и полупроводников (см. главу 4).
Во-вторых, с облегченным переносом заряда ионами вблизи вакансий в ионных кристаллах (и в меньшей степени межузельными ионами) по механизму схематически изображенному на рис. 2.3. Если вакансия 3, в которой должен был бы находиться положительный ион, оказывается во внешнем электрическом поле 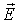 , то вероятность перескока в нее положительного иона в направлении 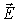 будет несколько выше, чем для иона в направлении, противоположном 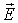 . В среднем положительно заряженные ионы буду перемещаться вдоль направления внешнего электрического поля и давать вклад в электропроводность. Аналогично, во внешнем электрическом поле 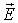 отрицательно заряженному иону выгоднее переместиться в вакансию в направлении противоположном 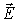 , чем в направлении поля 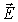 . Тогда отрицательно заряженные ионы будут перемещаться в направлении против поля 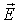 и также давать вклад в электропроводность. Во всех этих случаях вакансия как бы перемещается по кристаллу и обеспечивает перенос заряда, хотя фактически заряд переносят ионы, которые по-разному группируются вблизи вакансии. В таком случае говорят о вакансионном механизме переноса заряда подобно тому, как в главе 4 мы рассматривали дырочный механизм переноса заряда в полупроводниках. Перенос заряда по такому механизму требует преодоления значительно меньших потенциальных барьеров, чем, скажем, передача электрона от иона к иону.
Межузельзый ион 4 (см. рис. 2.3) также преимущественно перемещается (перескакивает) в направлении внешнего электрического поля 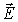 .
Влияние точечных дефектов на окраску кристаллов. Примесные атомы изменяют окраску кристаллов, например, примеси замещения - ионы хрома в кристаллах 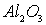 обеспечивают их красную окраску (получаются кристаллы рубина), ионы титана в кристаллах 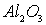 обеспечивают их голубую окраску (получаются кристаллы сапфира).
Методы изучения точечных дефектов. Число вакансий в единице объема можно оценить по сопоставлению результатов точного определения параметра решетки рентгеновским методом и точного определения плотности вещества как отношения его массы к объему. Метод основан на том, что вакансии крайне мало изменяют параметр решетки, но увеличивают объем кристалла, а значит уменьшают его плотность. Таким же способом, но с меньшей точностью, можно определить число межузельных атомов в единице объема, поскольку межузельные атомы несколько увеличивают плотность кристалла и слабее изменяют его параметр решетки. Если в кристалле присутствуют и вакансии и межузельные атомы, то описанным методом можно лишь оценить разность чисел вакансий и межузельных атомов в единице объема. Аналогично, плотность дефектов по Френкелю этим методом точно определить не удается.
Рассмотренные выше измерения электросопротивления и диффузии, а также измерения коэффициента поглощения различных электромагнитных излучений позволяют изучать точечные дефекты в кристаллах.
Задача 2.1. Вычислить равновесную концентрацию вакансий при температуре 300 и 900 К, если энергия образования вакансии равна 1 эВ.
Указание. Следует воспользоваться формулой (2.1).
Задача 2.2. Оценить глубину проникновения атомов углерода в поверхностный слой железа после выдержки при температуре 300 и 1500 К в течение 3 часов. Считать, что среда, содержащая углерод, вплотную прилегает к поверхности железа. Коэффициент диффузии вычислить по данным табл. 2.1. Такой способ насыщения поверхности углеродом, дополняемый последующей закалкой, используют для получения детали с твердой поверхностью и мягкой сердцевиной. Параметр решетки ОЦК -железа равен 0,288 нм.
Указание. Следует воспользоваться формулами (2.12) и (2.13).
|