6.4. Распределение Ферми-Дирака
Перейдем к анализу статистических свойств ферми-частиц, т.е. частиц, обладающих полуцелым спином. Напомним, что ферми-частицы подчиняются принципу (запрету) Паули, согласно которому в одном и том же состоянии одновременно не может находится более одного фермиона. Таким образом, фермионы являются частицами-индивидуалистами. Рассмотрим идеальный ферми-газ, т.е систему, состоящую из невзаимодействующих фермионов.
Как и в предыдущем параграфе решим сначала вспомогательную задачу - найдем число возможных распределений 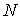 шаров по 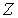 ячейкам пенала при условии, что в каждой ячейке не может находится более одного шара (рис. 6.5) . Темными кружками будем отмечать шары, находящиеся в ячейках, светлыми - отсутствие шара в ячейке. Число ячеек 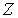 и число шаров 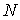 должны удовлетворять условию 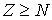 .
Число всевозможных перестановок черных и белых кружков по ячейкам пенала равно 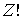 . При этом перестановки только черных кружков в силу тождественности частиц не приводят к новым распределениям. Число таких перестановок равно 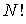 . Перестановки местами светлых кружков (пустых ячеек) тоже не дают новых распределений, их число равно 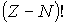 . Таким образом, число различных распределений 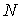 шаров по 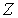 ячейкам в данном случае равно
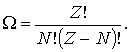 | (6.44) |
Для иллюстрации полученного результата рассмотрим распределение двух шаров по четырем ячейкам (рис.6.6). Число таких распределений равно
шести. Точно такой же ответ следует из (6.44)
Поскольку фермионы в силу запрета Паули являются частицами-индивидуалистами, то выражение (6.44) определяет число возможных распределений 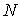 фермионов по 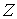 ячейкам, т.е. статистический вес макросостояния системы фермионов.
Вывод статистического распределения, которому подчиняются ферми-частицы, проводится подобно тому, как это было сделано выше для бозе-частиц. Рассмотрим шестимерное фазовое пространство с координатами 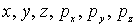 . Разобьем его с помощью изоэнергетических поверхностей
на тонкие энергетические слои, так что 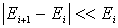 . Пусть в пределы 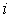 -го слоя попадает 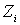 ячеек (каждая объемом 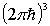 ) и 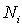 частиц. Тогда, согласно (6.44) , статистический вес подсистемы из 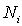 частиц есть
Статистический вес всей системы равен произведению статистических весов ее отдельных подсистем
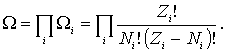 | (6.45) |
Для того, чтобы найти наиболее вероятное распределение частиц по ячейкам, нужно найти максимум статистического веса (6.45) при условии, что полное число частиц системы 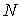 и полная энергия системы 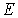 остаются постоянными, т.е.
Как и в случае бозе-частиц, вместо максимума статистического веса 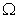 будем искать максимум энтропии 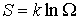 . С учетом (6.45) для энтропии системы ферми-частиц получаем следующее выражение
Воспользуемся формулой Стирлинга 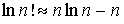 , справедливой при 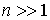 . Поскольку 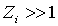 и 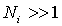 , то
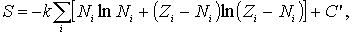 | (6.46) |
где 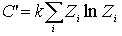 . Слагаемое 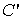 в (6.46) можно в дальнейшем не учитывать, поскольку при решении задачи на экстремум энтропии 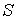 варьироваться будут только числа частиц в слое 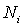 , а 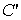 от них не зависит.
Для отыскания максимума энтропии (6.46) воспользуемся, как и в разделе 6.3, методом множителей Лагранжа. Рассмотрим функцию
где 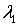 и 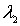 - множители Лагранжа. Приравнивая нулю частные производные этой функции по 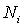 , получаем
Отношение 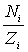 представляет собой среднее число ферми-частиц 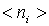 , приходящихся на одну ячейку, т.е. на одно квантовое состояние. Наиболее вероятное значение 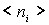 , как следует из решения задачи на экстремум, есть
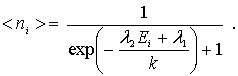 | (6.47) |
Множители Лагранжа 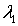 и 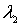 находятся точно также, как и в случае бозе-частиц. Используя тот же самый метод, что и в разделе 6.3 , для 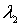 имеем
Записывая 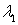 в виде 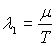 , где 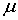 - химический потенциал, и подставляя 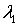 и 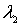 в (6.47) , получаем
Освобождаясь от индекса 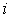 , приходим к окончательному выражению
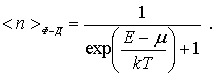 | (6.48) |
Соотношение (6.48) называется распределением Ферми-Дирака. Оно определяет среднее число ферми-частиц, находящихся в квантовом состоянии с энергией 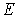 .
Обсудим следствия, вытекающие из распределения Ферми-Дирака. Прежде всего отметим, что 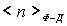 не может быть больше единицы, поскольку числитель выражения (6.48) равен единице, а в знаменателе к единице прибавляется положительная величина - экспонента. Это означает, что в одном квантовом состоянии не может находиться более одной ферми-частицы, что согласуется с принципом Паули. Поскольку 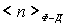 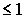 , то говорят, что распределение (6.48) определяет вероятность заполнения энергетического уровня с энергией 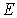 при температуре 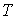 .
Химический потенциал 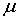 для ферми-частиц может быть только положительным, т.е. 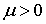 . Иначе при 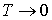 экспонента в знаменателе в (6.48) обратилась бы в бесконечность, а числа заполнения - в нуль, чего, естественно, быть не может. Напомним, что для бозе-частиц химический потенциал 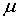 отрицателен.
Рассмотрим случай малых чисел заполнения, т.е. будем считать, что
Это условие выполняется при 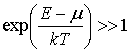 или 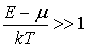 . Пренебрегая единицей по сравнению с экспонентой в знаменателе выражения (6.48) , получаем
где 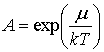 . Таким образом, мы приходим к заключению, что распределение Ферми-Дирака при малых числах заполнения, или, как говорят, в случае разреженного ферми-газа, переходит в классическое распределение Больцмана. В предыдущем параграфе было показано, что в распределение Больцмана в случае малых чисел заполнения переходит и распределение Бозе-Эйнштейна. Следовательно, можно сделать вывод, что разреженные квантовые газы (и в случае бозонов, и в случае фермионов) не являются вырожденными и подчиняются классической статистике. Подчеркнем, что хотя квантовая статистика в данном случае приводит к тем же результатам, что и классическая, квантовая природа частиц газа остается неизменной.
На рис. 6.7 приведены графики распределений Ферми-Дирака и Больцмана. При 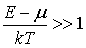 эти распределения, как уже отмечалось, совпадают. Кардинальное различие между ними наблюдается при 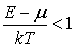 . Классические частицы могут накапливаться в одном и том же состоянии в большом количестве. Для них 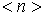 тем больше, чем меньше энергия состояния 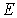 . Что же касается ферми-частиц, то максимальное
их число в одном квантовом состоянии не может превышать единицу, что согласуется с запретом Паули.
Химический потенциал 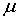 , который, как уже отмечалось, имеет размерность энергии, в случае ферми-частиц называют энергией Ферми или уровнем Ферми и обозначают 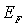 . При этом распределение Ферми-Дирака (6.48) принимает вид
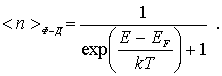 | (6.49) |
Именно это выражение мы и будем использовать в дальнейшем изложении.
Отметим, что поскольку для фермионов 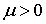 , то 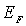 также больше нуля. В дальнейшем будет показано, что энергия Ферми 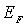 является медленно меняющейся функцией температуры 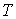 . Вид этой функции для электронного газа в металле рассмотрен в разделе 6.5 .
Для того, чтобы выявить физический смысл энергии Ферми, рассмотрим зависимость распределения Ферми-Дирака от температуры. Начнем наш анализ со случая 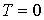 . Конечно, утверждение о том, что абсолютный нуль температур не достижим, остается в силе. Говоря о 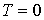 , мы будем считать, что рассматриваемая температура 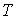 может быть сколь угодно близка к абсолютному нулю, т.е. 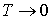 . Обозначим через 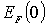 значение энергии Ферми при 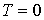 .
Из вида распределения (6.49) следует, что в случае 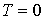
Это означает, что все квантовые состояния с энергиями 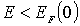 оказываются занятыми фермионами, а все состояния с энергиями 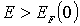 - свободными. Таким образом, при 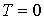 энергия Ферми 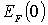 является максимальной энергией, которой могут обладать ферми-частицы.
График зависимости 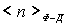 от 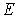 при 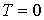 представлен на рис. 6.8.
Распределение Ферми-Дирака в этом случае представляет собой ступенчатую функцию единичной высоты, обрывающуюся при 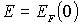 . Вид зависимости 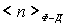 от энергии частиц 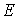 при температурах, отличных от нуля, приведен на рис. 6.9.
В этом случае резкий скачок 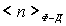 от единицы до нуля становится более размытым и происходит в области энергий, шириной порядка нескольких 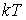 . Чем выше температура, тем шире область, в которой 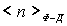 меняется от единицы до нуля, и тем более плавно происходит переход от заполненных состояний к незаполненным. Отметим, что, как следует из (6.49), при любой температуре значение 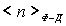 при 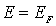 равно 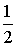 .
Наряду с энергией Ферми 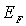 при анализе поведения ферми-частиц вводятся также импульс Ферми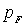 и скорость Ферми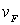 , определяемые соотношениями
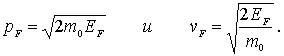 | (6.50) |
При 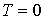 это максимальные импульс и скорость, которыми может обладать ферми-частица.
|