5.6. Атом в магнитном поле
Магнитный момент атома. В сложном многоэлектронном атоме каждый из 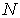 электронов обладает орбитальным и спиновым механическим и магнитным моментами. При сложении моментов отдельных электронов в результирующий момент атома возможны два случая.
1. Орбитальный и спиновой моменты каждого электрона складываются в результирующий момент, которые уже затем объединяются в суммарный момент атома. Такой вид связи называется  связью. Обычно такая связь наблюдается у тяжелых атомов.
2. Наиболее часто встречающаяся у атомов  связь ( связь Рассел - Саундерса) осуществляется по следующей схеме:
а) Все орбитальные механические моменты отдельных электронов складываются в орбитальный момент, величина которого
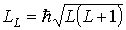 | (5.51) |
определяется квантовым числом 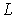 суммарного орбитального момента атома. Число 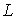 всегда является целым числом либо нулем.
б) Спиновые моменты импульса всех электронов многоэлектронного атома складываются в суммарный спиновой момент
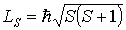 . . | (5.52) |
При этом в атомах с четным числом электронов квантовое число 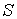 принимает все целые значения от нуля, когда спины электронов попарно компенсируют друг друга, до целого значения 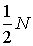 , когда спины всех электронов направлены в одну сторону. При нечетном 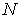 квантовое число 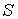 может принимать все полуцелые значения от 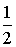 до 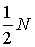 .
в) Результирующий момент всего атома 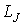 есть результат квантовомеханического сложения моментов 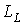 и  , которое сводится к правилу сложения квантовых чисел 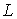 и 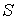 . Все возможные значения результирующего механического момента атома определяются формулой
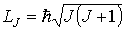 , , | (5.53) |
в которой квантовое число 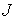 имеет одно из следующих значений
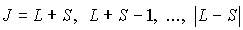 .
У атомов с четным числом электронов число 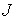 целое, а у атомов с нечетным числом электронов - полуцелое.
Проекция результирующего механического момента атома на выделенное направление 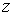 определяется следующей формулой пространственного квантования
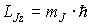 . . | (5.54) |
Здесь квантовое число  принимает 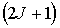 значений
Для обозначения квантовых чисел в многоэлектронном атоме используется условное обозначение "терма" атома в определенном квантовом состоянии в виде
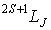 ,
где под 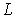 подразумевается одна из букв следующей таблицы *
L | 0 | 1 | 2 | 3 | 4 | ... |
| S | P | D | F | D | ... |
Терм содержит в себе сведения о значении трех квантовых чисел 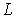 , 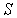 и 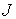 . Например, для терма 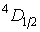 значения этих чисел: 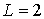 , 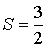 и  , а для 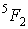 , соответственно, 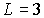 , 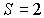 и 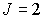 .
Число 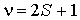 называется мультиплетностью терма. В случае, когда 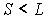 , это число дает количество подуровней, отличающихся значением числа 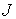 .
Гиромагнитное отношение для суммарных механического и магнитного моментов многоэлектронного атома отличается как от орбитального (5.39), так и от спинового (5.46). Соответствующий квантовомеханический расчет дает для суммарного магнитного момента атома выражение
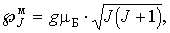 | (5.55) |
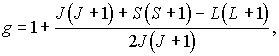 | (5.56) |
зависящий от всех трех квантовых чисел 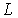 ,  и 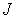 , называется фактором Ланде.
Анализ (5.56) показывает, что множитель Ланде может иметь значения, меньшие единицы, и даже быть равным нулю (например, когда 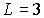 , а 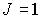 ). Последнее означает, что у многоэлектронного атома магнитный момент может быть равным нулю, даже если механический момент отличен от нуля.
При расчетах полезно помнить, что  , если результирующий спин 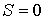 , и 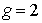 , если 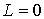 .
Проекция суммарного магнитного момента атома на выделенное направление 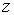 внешнего магнитного поля, определяется формулой
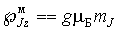 . . | (5.57) |
Для заданного значения 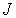 существует 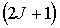 различных ориентаций магнитного момента атома по отношению к внешнему магнитному полю.
Квантовая теория обосновывает правила отбора для квантовых чисел 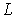 , 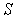 и 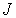 при переходах атома из одного квантового состояния в другое. Существенно отличные от нуля вероятности имеют только такие переходы, в которых
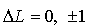 ,
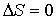 ,
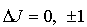 .
Эффект Зеемана. При помещении магнитного момента 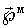 во внешнее магнитное поле с индукцией 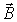 , он приобретает дополнительную энергию за счет магнитного взаимодействия
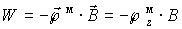 . . | (5.58) |
Поэтому, если изолированный атом с энергией 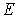 в состоянии с квантовым числом 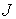 попадает в магнитное поле, то энергия уровня 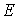 изменяется так, что это изменение, в зависимости от взаимной ориентации магнитного момента и поля, соответствует одному из 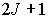 возможных значений
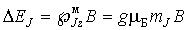 . . | (5.59) |
В системе излучающих атомов (газе), помещенной в магнитное поле, появятся атомы с различными энергиями исходного уровня. Эту ситуацию удобнее описать, рассмотрев расщепление энергетического уровня атома на  эквидистантных подуровня с расстоянием между соседними подуровнями
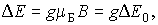 | (5.60) |
где  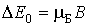 - величина нормального расщепления энергетического уровня.
Следствием этого является расщепление спектральных линий излучения газа атомов, помещенного в магнитное поле, которое впервые наблюдал П.Зееман в 1896 г. при исследовании свечения паров натрия в магнитном поле. Поэтому такой эффект расщепления спектральных линий в магнитном поле получил название эффекта Зеемана.
Наиболее простой случай соответствует расщеплению одиночной линии, обусловленной переходами между энергетическими уровнями, для которых 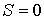 . Для этого случая 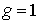 и поэтому 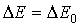 при расщеплении каждого уровня. При внесении таких атомов в магнитное поле исходная спектральная линия с частотой 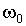 расщепляется на три линии с частотами 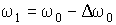 , 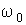 , 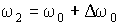 . При этом смещение частоты
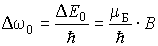 | (5.61) |
называется нормальным смещением. Величина такого смещения пропорциональна индукции внешнего магнитного поля, причем для  Тл 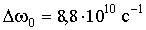 . В области видимого света это соответствует  нм.
Такой случай расщепления спектральной линии на зеемановский триплет называется простым или нормальным эффектом Зеемана.
Все три линии зеемановского триплета наблюдаются, если направление наблюдения перпендикулярно магнитному полю. При наблюдении вдоль поля несмещенная линия с частотой 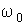 не наблюдается.
Для примера на рис. 5.11 изображен нормальный эффект Зеемана для перехода между уровнями с  и 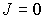 . Уровни с другими значениями 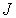 расщепляются на большее число подуровней. Так, например, уровень с 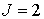 расщепляется на пять подуровней. Однако, и в этом случае, если для обоих уровней 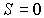 , в магнитном поле будет наблюдаться расщепление спектральной линии только на три. Это объясняется тем, что для оптических переходов число  подчиняется правилу отбора: 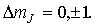
Для переходов между уровнями с  у расщепленной спектральной линии оказывается больше трех компонент, а величина расщепления отличается от нормального. Это связано с зависимостью фактора Ланде 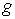 от значения всех трех квантовых чисел  ,  и 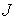 . Такое расщепление спектральных линий при помещении излучающих атомов в магнитное поле называется сложным или аномальным эффектом Зеемана.
В сильном магнитном поле, когда магнитное расщепление линий становится больше спин-орбитального расщепления, связь между орбитальными и спиновыми магнитными моментами разрывается и в результате для любых переходов наблюдается нормальный зеемановский триплет. Это явление называется эффектом Пашена-Бака.
Электронный парамагнитный резонанс. Из формулы (5.60) следует, что при помещении атома в магнитное поле с индукцией  Тл энергетические уровни атома расщепляются на подуровни, отличающиеся по энергии на величину порядка 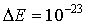 Дж. Длина волны излучения, соответствующая переходу между такими подуровнями составляет несколько сантиметров. Это излучение находится в микроволновой области радиодиапазона.
Следовательно, в веществе, помещенном в сильное магнитное поле, можно инициировать переходы между зеемановскими подуровнями, если облучать вещество радиочастотным полем. При этом вещество должно сильно поглощать микроволновое излучение на резонансной частоте
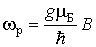 . . | (5.62) |
Это явление было обнаружено Е.К.Завойским в 1944 г. и получило название электронного парамагнитного резонанса (ЭПР).
В таком опыте (рис. 5.12) исследуемое парамагнитное вещество (у диамагнетиков магнитные моменты атомов близки к нулю) объемом в несколько мм 3 помещают в резонатор Р, настроенный на частоту  Гц и помещенный между полюсами электромагнита. Радиочастотное излучение, создаваемое генератором Г, подводится и отводится от резонатора с помощью волноводов. Приемник П настраивается на частоту генератора.
Плавным изменением индукции магнитного поля электромагнита можно добиться условия  . При этом за счет ЭПР вещество начинает сильно поглощать радиочастотное излучение. Резонансное поглощение энергии уменьшает амплитуду сигнала в приемнике, которое фиксируется регистрирующим устройством РУ. При этом обычно на экран осциллографа выводится зависимость коэффициента поглощения от отношения частот 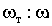
ЭПР находит широкое применение в экспериментальной физике. Из условия резонанса можно получить величину  - фактора, а с ней определить электронную структуру атома и его магнитный момент. В твердых телах и жидкостях ЭПР является эффективным методом изучения взаимодействия частиц. По спектрам ЭПР можно определить структуру кристаллов, природу и локализацию дефектов кристаллической решетки. Методы электронного парамагнитного резонанса широко применяется в химии и биологии для изучения свободных радикалов и ферментов.
На основе электронного парамагнитного резонанса созданы квантовые магнетометры - приборы для прецизионного измерения слабых магнитных полей.
Отметим, что в настоящее время обнаружены другие виды магнитного резонанса - ферромагнитный резонанс (ФРМ) и ядерный магнитный резонанс (ЯМР). В ФМР используются переходы между подуровнями веществ с ферромагнитной структурой. ЯМР обусловлен переходами между зеемановскими подуровнями ядер атомов в сильных магнитных полях.
Задача 5.6. Найдите механический момент атома, находящегося в состоянии с  и 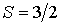 , если известно, что магнитный момент атома равен нулю.
Решение: При заданных значениях  и 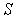 квантовое число 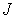 не может быть равно нулю. Поэтому магнитный момент атома равен нулю за счет равенства нулю фактора Ланде 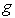 . Если ввести обозначение 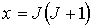 , то условие 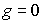 приведет к соотношению
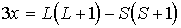 .
Для 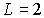 и 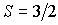 отсюда находим, что 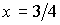 и 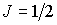 . Поэтому величина механического момента атома
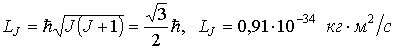 .
Задача 5.7. Найдите минимальное значение индукции магнитного поля, при которой спектральным прибором с разрешающей способностью 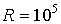 можно разрешить все компоненты спектральной линии 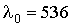 нм при ее расщеплении в простом эффекте Зеемана.
 ,
то длины волн зеемановского триплета будут отличаться на величину
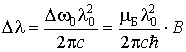 .
Разрешающая способность спектрального прибора
 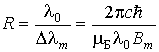 .
Отсюда находим минимальное значение индукции магнитного поля
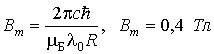 .
* не путать символ S с суммарным спиновым квантовым числом.
|