5.5. Опыт Штерна и Герлаха. Гипотеза о спине электрона
Опыт Штерна и Герлаха. Оптические эксперименты дают вполне достаточные доказательства квантования энергии атомов. Другой вид квантования - пространственное квантование, утверждающее дискретность проекции магнитного момента атома на направление внешнего магнитного поля, демонстрируется экспериментом с атомными пучками, выполненным О.Штерном и В.Герлахом в 1922 г.
Для атома водорода пространственное квантование орбитального магнитного момента описывается формулой (5.42). Для более сложных многоэлектронных атомов эта формула несколько видоизменяется (см. раздел 5.6). Однако и для таких атомов остается в силе основной вывод квантовой теории: проекция магнитного момента атома на направление внешнего магнитного поля может иметь только дискретные квантовые значения.
В опыте Штерна и Герлаха пространственное квантование для атомных систем демонстрируется следующим образом. Путем испарения в вакуумной печи атомов серебра или другого металла с помощью тонких щелей формируется узкий атомный пучок (А.П. на рис. 5.10а). Этот пучок пропускается через неоднородное магнитное поле с существенным градиентом магнитной индукции. Индукция магнитного поля  в опыте велика и направлена вдоль оси 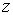 .
Для создания такого магнитного поля используется магнит с ножевидным полюсным наконечником (рис. 5.10б), вблизи которого на достаточно малом расстоянии пропускается атомный пучок.
На пролетающие в зазоре магнита атомы вдоль направления магнитного поля действует сила
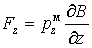 , , | (5.43) |
обусловленная градиентом индукции неоднородного магнитного поля и зависящая от величины проекции магнитного момента атома на направление поля. Эта сила отклоняет движущийся атом в направлении оси 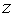 , причем за время пролета магнита движущийся атом отклоняется тем больше, чем больше величина силы (5.43). При этом одни атомы отклоняются вверх, а другие вниз.
С позиций классической физики, магнитный момент атомов вследствие их хаотичного теплового движения, при влете в магнитное поле может иметь любое направление в пространстве. Это соответствует непрерывному распределению значений 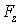 для различных атомов и, соответственно, любым различным отклонениям атомов. В результате, пролетевшие через магнит атомы серебра должны были образовать сплошную широкую зеркальную полосу на стеклянной пластинке.
Если же, как предсказывает квантовая теория, имеет место пространственное квантование, и проекция магнитного момента  атома принимает только определенные дискретные значения, то под действием силы (5.43) атомный пучок должен расщепиться на дискретное число пучков, которые, оседая на стеклянной пластинке, дают серию узких дискретных зеркальных полосок из напыленных атомов. Именно этот результат наблюдался в эксперименте.
Таким образом, опыт Штерна и Герлаха доказал правильность выводов квантовой теории о наличии пространственного квантования магнитных моментов атомов.
Спин электрона. Из квантовой теории следует, что вследствие симметрии электронного "облака" механический и магнитный моменты атома, находящегося в основном, невозбужденном состоянии, равны нулю. Следовательно, если в опыте Штерна - Герлаха обеспечить условия, при которых в атомном пучке будут двигаться невозбужденные атомы, то такой атомный пучок не должен расщепляться магнитным полем. Поэтому на стеклянной пластинке мы увидели бы в центре одну узкую зеркальную полоску.
Однако, эксперимент не подтвердил такой вывод квантовой теории. Пучок невозбужденных атомов серебра расщепился на два пучка, которые напылили на стеклянной пластинке две узкие зеркальные полоски, сдвинутые симметрично вверх и вниз. Измерение этих сдвигов позволило определить магнитный момент невозбужденного атома серебра. Его проекция на направление магнитного поля оказалась равной 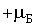 или 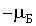 .
Это противоречие квантовой теории и опыта было не единственным, обнаруженным к этому времени в различных экспериментах. Такое же отличие наблюдалось при изучении тонкой структуры оптических спектров щелочных металлов. В опытах с ферромагнетиками было обнаружено аномальное значение гиромагнитного отношения, отличающегося от ожидаемого значения (5.39) в два раза.
Все эти трудности квантовой теории были преодолены, когда в 1925 г. С.Гаудсмит и Дж.Уленбек выдвинули смелую теорию о том, что сам электрон является носителем "собственных" механического и магнитного моментов, не связанных с движением электрона в пространстве. Эта гипотеза получила название гипотезы о спине электрона. Такое название связано с английским словом 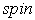 , которое переводится как "кружение", "верчение".
Первоначально предполагалось, что спин обусловлен вращением электрона вокруг своей оси. Однако, такая модель вращающегося заряженного шарика оказалась несостоятельной. Прежде всего, расчет показал, что ни при каких допустимых (т.е. меньше скорости света) скоростях нельзя вращением электрона индуцировать магнитный момент, равный по величине магнетону Бора. Кроме того, величина гиромагнитного отношения собственного магнитного и механического моментов, рассчитанная для модели вращающегося электрона, оказалась в два раза меньше, чем получаемая в опытах.
Модель электрона, вращающегося вокруг своей оси, как вращается Земля, двигаясь по околосолнечной орбите, в настоящее время может использоваться только при популярном изложении свойств атома. Однако термин "спин" сохранился и является общепринятым в современной квантовой физике.
Спин электрона не имеет классического аналога. Он характеризует внутреннее свойство квантовой частицы, связанное с наличием у нее дополнительной степени свободы. Количественная характеристика этой степени свободы - спин 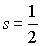 является для электрона такой же величиной как, например, его масса 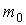 и заряд 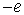 .
При согласовании теории и эксперимента Гаудсмит и Уленбек, по аналогии с орбитальными моментами, предположили, что величины собственных механического и магнитного моментов электрона определяются формулами
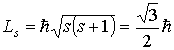 , , | (5.44) |
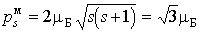 . . | (5.45) |
Для таких моментов гиромагнитное отношение
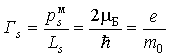 | (5.46) |
оказывается в два раза большим гиромагнитного отношения для орбитального движения (5.39).
Проекции собственных моментов на выделенное направление 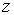 в такой теории определяются спиновым квантовым числом . При этом
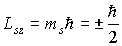 , , | (5.47) |
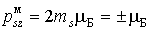 . . | (5.48) |
Из (5.44 - 5.48) следует, что величина спиновых моментов электрона постоянна, а с дополнительной степенью свободы электрона связаны 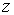 -проекции этих моментов, которые определяются спиновым квантовым числом  и принимают два значения. О таких двух квантовых состояниях обычно говорят как о состояниях со спином, направленным вверх 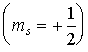 или вниз  . Поэтому, определяя квантовое состояние электрона в любой системе следует указать также и ориентацию спина.
В частности, это означает, что квантовое состояние электрона в атоме следует определять набором четырех квантовых чисел.
Название | Символ | Возможные значения |
Главное квантовое число | | 1, 2, 3, ... |
Орбитальное квантовое число | | 1, 2, 3, ... 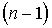 |
Магнитное квантовое число | | 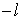 , ...., -2, -1, 0, +1, +2, ... ,  |
Спиновое квантовое число | | |
При этом каждому значению главного квантового числа  соответствует
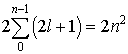 | (5.49) |
возможных комбинаций других квантовых чисел.
С учетом наличия у электрона спина, найдем результирующий полный момент импульса атома водорода, обусловленный сложением орбитального и собственного моментов электрона. Как и для любого момента импульса в квантовой системе, величина результирующего момента определяется выражением
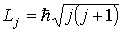 | (5.50) |
в котором квантовое число 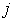 может иметь значения
 .
Так как спин электрона  , то получаем полуцелые значения
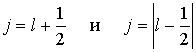 .
Если 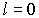 , то квантовое число  имеет только одно значение, равное  . При 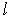 , отличном от нуля, возможны два значения 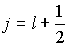 и 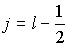 , которые соответствуют двум различным ориентациям спинового момента относительно орбитального.
Для квантового числа полного момента импульса атома выполняется правило отбора
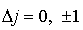 .
С механическими моментами связаны магнитные моменты, которые взаимодействуют друг с другом подобно тому, как взаимодействуют два замкнутых тока. Это взаимодействие называется спин-орбитальным. Оно изменяет полную энергию атома и, следовательно, в квантовых состояниях с различными  атом должен обладать различными энергиями. Такое различие в энергиях приводит к расщеплению линий в оптическом спектре атома. Это расщепление очень мало. Оно обуславливает тонкую структуру оптического спектра атома водорода, в которой спектральные линии наблюдаются как дублетные (двойные). И хотя расстояние между линиями тонкой структуры в сотни тысяч раз меньше расстояний между основными линиями, тонкая структура водородного спектра была обнаружена экспериментально с помощью спектральных приборов с большой разрешающей способностью.
Какова же физическая природа наличия у электрона спина? Ответа на этот вопрос нет не только к классической физике, но и рамках нерелятивистской квантовой механики, в основе которой лежит уравнение Шредингера. В такой теории спин вносится в виде дополнительной гипотезы, не вытекающей из основных положений теории, но необходимой для согласования эксперимента и теории.
В 1928 г. П.Дирак обобщил квантовую теорию на случай релятивистского движения частицы. В основе релятивистской квантовой механики лежит уравнение Дирака, записанное первоначально для релятивистского электрона. Это уравнение значительно сложнее уравнения Шредингера по своей структуре и математическому аппарату, используемому при его записи. В рамках нашего курса мы не имеем возможности обсуждать это уравнение. Скажем лишь, что из уравнения Дирака четвертое, спиновое квантовое число получается так же естественно, как и три квантовых числа при решении уравнения Шредингера.
Релятивистская квантовая теория дает, в частности, для расстояния между энергетическими уровнями, обуславливающими тонкую структуру водородного спектра, значение
 ,
где 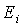 - энергия ионизации атома водорода, а  универсальная мировая константа, которая получила название постоянной тонкой структуры.
Итак, в самых общих словах можно сказать, что собственные механический и магнитный моменты у электрона появляются как следствие релятивистских эффектов в квантовой теории.
Отметим также, что не только электрон, но и многие другие элементарные частицы обладают спином 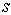 , имеющим целые значения для одних частиц и полуцелые значения для других. Так, например, составные частицы ядер атомов - нейтрон и протон имеют спин 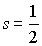 . Поэтому и ядро атома водорода обладает механическим и магнитным моментами. Взаимодействием магнитных моментов электрона и ядра объясняется сверхтонкая структура оптического спектра с дополнительным "сверхмалым" расщеплением спектральных линий.
Задача 5.5. Атом водорода в основном состоянии находится на оси кругового тока 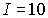 А радиуса  см. Расстояние атома до центра кругового тока 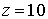 см. Определите силу, действующую на атом со стороны магнитного поля тока в вакууме с учетом спина электрона. Магнитный момент ядра не учитывать.
Решение: Индукцию магнитного поля на оси кругового тока на расстоянии  от его центра определим по известной формуле магнитостатики
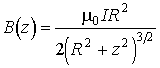 .
Дифференцируя 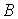 по переменной  , находим величину градиента индукции магнитного поля на расстоянии  от центра кругового тока
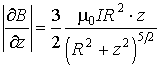 .
Если не учитывать магнитный момент ядра, то магнитный момент атома водорода в 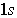 - состоянии (  ) обусловлен только спином электрона. Поэтому
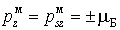 .
Следовательно, на атом со стороны магнитного поля тока будет действовать сила, модуль которой
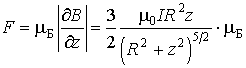 .
Эта сила направлена вдоль оси кругового тока к его центру, если магнитный момент электрона параллелен магнитному полю, и от центра, если направление спина противоположно. Подставляя числовые значения, находим, что  .
|