5.2. Теория Бора атома водорода
Постулаты Бора. В 1911 г. после проведения опытов по рассеянию альфа-частиц на атомах Дж.Резерфорд на основании анализа результатов эксперимента выдвинул и обосновал планетарную модель строения атома. Согласно этой модели атом состоит из тяжелого положительно заряженного ядра очень малых размеров ( 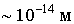 ), вокруг которого по некоторым орбитам движутся электроны. Радиусы этих орбит составляют порядка 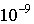 м. Название "планетарная" у такой модели атома отражает очевидную аналогию атома с Солнечной системой, в которой планеты движутся по некоторым определенным орбитам вокруг массивного притягивающего центра - Солнца.
Однако, в отличие от планетарной модели Солнечной системы, планетарная модель атома оказывается внутренне противоречивой с точки зрения классической физики. И это, прежде всего, связано с наличием у электрона заряда.
Согласно законам классической электродинамики вращающийся вокруг ядра электрон, как и любая ускоренно движущаяся заряженная частица, будет излучать электромагнитные волны. Спектр такого излучения должен быть непрерывным, то есть содержать электромагнитные волны с любой длиной волны. Уже этот вывод противоречит линейчатости спектров излучения атомов, наблюдаемой на опыте.
Кроме того, непрерывное излучение уменьшает энергию электрона. Поэтому, за счет излучения радиус орбиты движущегося электрона обязан уменьшаться, и, в конце концов, электрон должен упасть на ядро. Иными словами, планетарная модель атома в классической физике оказывается неустойчивой.
В 1913 г. Н.Бор показал, что "спасти" планетарную модель атома можно, вводя в теорию атома идеи квантования и выделяя при этом некоторые орбиты, разрешенные для движения электрона. Очевидно, что в правилах квантования должна фигурировать квантовая постоянная Планка. И так как квант действия 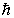 имеет размерность момента импульса, то Бор добавляет в теорию условие квантования момента импульса движущегося вокруг ядра электрона.
Простейшим атомом является атом водорода, содержащий один единственный электрон, движущийся по замкнутой орбите в кулоновском поле ядра. В первом приближении ядро атома можно считать неподвижным, а электронные орбиты - круговыми орбитами.
При этих предположениях Бор сформулировал основные положения теории атома водорода в виде трех постулатов.
1. Электрон в атоме может двигаться только по определенным стационарным орбитам, каждой из которых можно приписать определенный номер 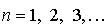 . Такое движение соответствует стационарному состоянию атома с неизменной полной энергией 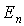 . Это означает, что движущийся по стационарной замкнутой орбите электрон, вопреки законам классической электродинамики, не излучает энергии.
2. Разрешенными стационарными орбитами являются только те, для которых угловой момент импульса  электрона равен целому кратному величины постоянной Планка электрона равен целому кратному величины постоянной Планка 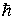 . Поэтому для  -ой стационарной орбиты выполняется условие квантования
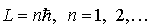 . . | (5.3) |
3. Излучение или поглощение кванта излучения происходит при переходе атома из одного стационарного состояния в другое (рис. 5.4). При этом частота  излучения атома определяется разностью энергий атома в двух стационарных состояниях, так что
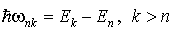 . . | (5.4) |
Квантование энергии атома. Запишем условие вращения электрона массы 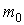 по круговой орбите радиуса 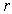 под действием кулоновской силы со стороны ядра и формулу Бора квантования момента импульса электрона
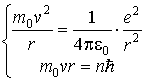 . . | (5.5) |
Решая эту систему уравнений, находим для радиусов допустимых (стационарных) орбит электрона в атоме водорода следующее выражение
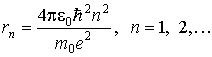 . . | (5.6) |
Вводя в качестве универсальной константы теории боровский радиус
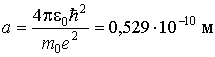 | (5.7) |
как радиус первой стационарной орбиты электрона в атоме водорода, запишем формулу (5.6) в виде
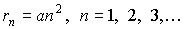 . . | (5.8) |
Важно отметить, что оценка размера атома водорода (  ), полученная из (5.7) и (5.8), совпадает с соответствующей оценкой из газокинетической теории.
Для скорости электрона на 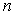 -ой стационарной орбите из (5.5) получаем значение
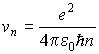 . . | (5.9) |
Отсюда находим, в частности, что на первой стационарной орбите электрон движется со скоростью  м/с, совершая один полный оборот за время 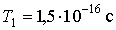 .
Полная энергия электрона, движущегося по  -ой стационарной орбите, складывается из его кинетической энергии
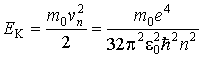 | (5.10) |
и потенциальной энергии кулоновского взаимодействия электрона с ядром
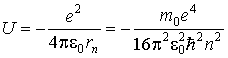 . . | (5.11) |
Поэтому, с учетом (5.10) и (5.11), получаем важную формулу теории Бора - формулу квантования энергии электрона в атоме водорода
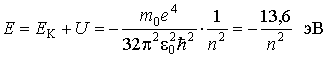 . . | (5.12) |
Полная энергия электрона в атоме оказалась отрицательной, так как, по определению, отрицательна потенциальная электростатическая энергия взаимодействия электрона с ядром. С ростом номера орбиты полная энергия электрона в атоме возрастает. При этом номер орбиты 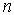 является квантовым числом в такой теории.
На рисунке 5.5 в соответствии с (5.12) изображен энергетический спектр электрона в атоме водорода. В области положительных энергий энергетический спектр свободного электрона является сплошным спектром. В области отрицательных значений полной энергии энергетический спектр связанного с атомом электрона становится дискретным. Для наглядности на рис. 5.5 каждому возможному значению энергии соответствует энергетический уровень. В стационарном состоянии электрон может находится на одном из этих дискретных энергетических уровней. Переход электрона с одного уровня на другой на этом рисунке может быть изображен соответствующей стрелкой, начало и конец которой указывают энергетические уровни, между которыми происходит переход.
Обычно атом находится в основном состоянии с наименьшим значением энергии, равным  . В этом состоянии атома электрон движется по первой стационарной орбите, имеющей минимальный радиус, равный  .
Если атому сообщить дополнительную энергию, то он может перейти в возбужденное состояние (переход 1 на рис. 5.4). Электрон при этом переходит на орбиту большего радиуса. Возбуждение атомов может инициироваться различными способами, например, столкновением атомов газа в хаотическом тепловом движении, пропусканием через газ потока высокоэнергетических частиц (электронов, альфа-частиц и др.) и, наконец, поглощением атомами излучения.
Если энергия, переданная электрону будет достаточно велика, то электрон может преодолеть силу притяжения к ядру и оторваться от атома. Такой процесс называют ионизацией атома. Из рис. 5.4 видно, что минимальная энергия, необходимая для ионизации атома водорода (переход 2), равна
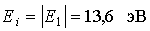 . . | (5.13) |
Это значение хорошо согласуется с экспериментальными данными для энергии ионизации атома водорода.
В возбужденном состоянии атом долго находиться не может. Как и любая физическая система, атом стремится занять состояние с наименьшей энергией. Поэтому через время порядка 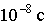 возбужденный атом самопроизвольно (спонтанно) переходит в состояние с меньшей энергией, испуская при переходе квант энергии излучения. Такой процесс продолжается до тех пор, пока атом не окажется в основном состоянии.
Если определена структура энергетических уровней, то можно рассчитать и структуру спектра излучения атома водорода. Действительно, частоту излучения при переходе электрона с  -ой более удаленной орбиты на 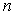 -ую ( 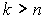 ) можно определить, используя третий постулат теории Бора. С учетом (5.4) и формулы квантования энергии (5.12) получаем выражение для частот излучения атома водорода при различных переходах 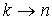 :
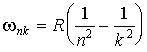 . . | (5.14) |
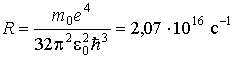 | (5.15) |
точно соответствует по величине постоянной Ридберга, найденной из оптических экспериментов.
Полученная формула для частот излучения атома водорода точно совпадает с обобщенной формулой Бальмера (5.1 а). Не удивительно, поэтому, что теория Бора атома водорода, в основе которой лежит постулат квантования (5.3), в 1922 г. была удостоена Нобелевской премии по физике.
Изложенная выше теория может быть обобщена на случай эллиптических орбит (Теория Бора-Зоммерфельда, 1915 г.) и для описания свойств любых "водородоподобных" атомов - атомных систем, содержащих один электрон, движущийся в поле ядра с положительным зарядом 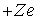 . Это однократно ионизированный гелий 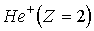 , двукратно ионизированный литий 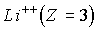 , трехкратно ионизированный бериллий 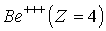 и т.д. Простой пересчет показывает, что энергетический спектр водородоподобного иона получается из (5.12) умножением на  , а радиус орбит электрона оказывается в  раз меньше, чем в атоме водорода.
Н.Бор в своей теории атома водорода впервые реализовал идею квантования энергии частицы, движущейся в силовом поле. Однако, эта теория не может рассматриваться как законченная теория атомных явлений. Описывая атом законами классической физики, Бор просто "запретил" электрону, движущемуся по стационарной орбите, излучать электромагнитные волны. При этом условие квантования момента импульса электрона (5.3) не имеет общего физического обоснования, и фактически, угадано (в дальнейшем будет показано даже, что угадано не совсем верно) для атома водорода. Попытки Бора обобщить теорию и сформулировать постулаты квантования для более сложных атомов не увенчались успехом.
С позиции современной физики, атом является физической системой, которая, заведомо, не может быть описана классической теорией, не учитывающей волновых свойств движущегося в атоме электрона.
В последующих параграфах настоящей главы будет рассмотрено, как современная квантовая теория формулирует и решает проблему описания атомных систем.
Задача 5.1. Покажите, как условие квантования момента импульса электрона в теории Бора атома водорода можно сформулировать с учетом гипотезы де Бройля о наличии у электрона волновых свойств.
Решение: Для электрона, движущегося по круговой орбите радиуса  , момент импульса 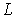 связан с импульсом  простым соотношением: 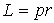 . Поэтому, условие квантования (5.3) можно преобразовать к виду
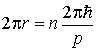 .
Согласно гипотезе де Бройля движение электрона следует связать с волновым процессом, длина волны которого
  .
Поэтому условие квантования Бора можно записать как
 .
Это соотношение утверждает, что стационарными являются только такие орбиты, на длине которых укладывается целое число длин волн де Бройля для движущегося по орбите электрона.
Задача 5.2. Покажите, как изменятся частота излучения атома водорода с учетом конечной величины массы ядра.
Решение: В такой постановке задачи электрон и ядро вращаются вокруг неподвижного центра масс. Если через 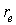 и  обозначить радиусы круговых орбит электрона и ядра, то по определению центра масс:  , где 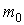 и 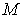 , соответственно, массы электрона и ядра.
Из равенства ускорений электрона и ядра вытекает условие равенства их угловых скоростей вращения
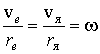 ,
где  и  - скорости электрона и ядра, соответственно.
С учетом движения ядра, момент импульса атома
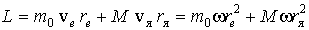 .
В качестве основных уравнений теории запишем условие вращения электрона по круговой орбите и и условие Бора квантования момента импульса атома
Если расстояние между электроном и ядром обозначить через 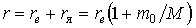 , то после преобразований эти соотношения запишутся в виде
Здесь введена приведенная масса системы "электрон-ядро"
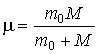 .
Решая полученную систему уравнений, находим для стационарных состояний атома ( 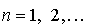 )
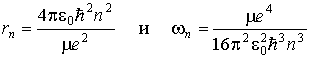 .
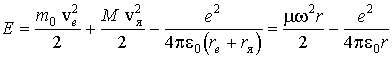 .
Подставляя сюда значения 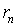 и 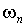 , получаем формулу квантования энергии атома
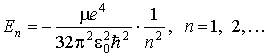 .
Отсюда находим частоты спектральных линий излучения такого атома:
 ,
где модифицированная постоянная Ридберга
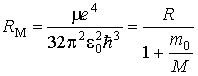 .
Расчет показывает, что поправка частоты (или длины волны) излучения атома водорода за счет учета движения ядра составляет доли процента. Однако, благодаря чрезвычайной точности спектроскопических методов, появляется возможность экспериментально обнаружить различие в спектрах излучения изотопов водорода - атомов, отличающихся массами ядер. Практически, именно так, спектроскопическими методами был открыт изотоп тяжелого водорода - дейтерий  , для которого 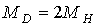 .
|