4.3. Движение частицы в области потенциального порога и барьера
В предыдущем параграфе было рассмотрено движение частицы в ограниченной области пространства, так называемое финитное движение. Перейдем теперь к анализу случаев, в которых частица , находящаяся в силовых полях, способна уходить на бесконечность, т.е. приступим к рассмотрению инфинитного движения частицы.
Движение частицы в области потенциального порога. Рассмотрим движение частицы в силовом поле, в котором ее потенциальная энергия 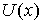 имеет вид
В этом случае говорят, что частица находится в области потенциального порога. На границе порога, т.е при 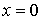 , потенциальная энергия частицы скачком меняется на конечную величину 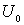 (рис.4.7) .
Обозначим область слева от порога ( 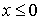 ) цифрой I и все решения для этой области будем отмечать индексом 1 . Область справа от порога ( 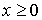 ) обозначим цифрой II , будем отмечать соответствующие ей решения цифрой 2 .
Уравнение Шредингера для частицы в таком силовом поле имеет вид:
Рассмотрим сначала случай, когда энергия частицы 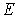 меньше высоты потенциального порога 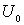 , т.е. 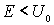 . Говорят, что в этом случае мы имеем дело с высоким потенциальным порогом. Вводя обозначения
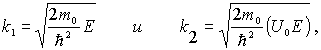 | (4.29) |
получаем уравнения Шредингера для областей I и II в виде
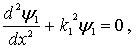 | (4.30a) |
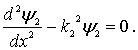 | (4.30b) |
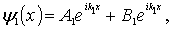 | (4.31a) |
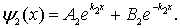 | (4.31b) |
Отметим, что полученные волновые функции 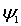 и 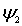 , описывающие состояние частицы в областях I и II , в случае высокого потенциального порога имеют существенно различный вид. Первое слагаемое в волновой функции 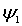 представляет собой плоскую волну де Бройля, распространяющуюся вдоль оси 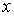 из 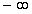 к области порога, т.е. слева направо. Аналогично, второе слагаемое в 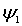 описывает плоскую дебройлевскую волну, распространяющуюся вдоль оси 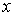 в отрицательном направлении.
В том, что выражение 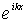 действительно описывает плоскую волну, легко убедиться, вспомнив про временной множитель 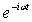 для волновой функции в стационарном состоянии (4.8) . Умножая 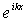 на 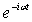 , получаем 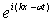 , т.е. плоскую волну де Бройля, распространяющуюся вдоль оси 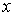 в положительном направлении. Аналогично, 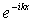 представляет плоскую волну де Бройля, распространяющуюся вдоль оси 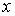 в отрицательном направлении.
Таким образом, волновая функция 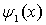 в виде (4.31a) представляет собой сумму падающей на порог и отраженной от него плоских волн де Бройля. Тогда как волновая функция 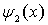 , характеризующая движение частицы в области II , представляет собой сумму двух экспонент (4.31b) с действительными показателями степени.
Воспользуемся теперь условиями, налагаемыми на волновую функцию. Поскольку волновая функция должна быть ограниченной, а первое слагаемое в волновой функции 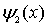 при 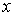 , стремящемся к бесконечности, неограниченно возрастает, то необходимо потребовать, чтобы коэффициент 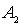 перед этим слагаемым был равен нулю. Далее, в силу того, что высота порога  имеет конечную величину, волновая функция на границе раздела областей I и II должна быть не только непрерывной, но и гладкой, т.е. иметь непрерывную производную. Приравнивание волновых функций и их производных на границе раздела двух областей, в которых волновая функция имеет разный вид, получило название сшивки волновых функций и их производных. В данном случае условия сшивки имеют вид
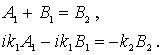 | (4.32) |
Система уравнений (4.32) позволяет выразить коэффициенты 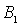 и  через коэффициент 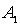 , т.е. через амплитуду падающей на порог волны де Бройля. Поскольку в подобных задачах все имеющие физический смысл величины, такие, например, как коэффициент отражения частицы от порога, коэффициент прохождения и т.д. выражаются через отношение коэффициентов 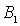 и 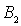 ( или аналогичных им ) к 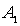 , то без потери общности можно положить 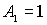 . При этом для 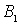 и 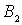 из (4.32) получаем
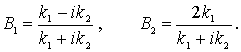 | (4.33) |
Таким образом, волновые функции частицы в случае высокого порога имеют вид
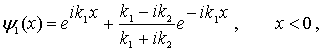 | (4.33a) |
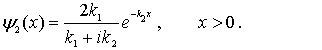 | (4.33b) |
Отметим, что система уравнений (4.32) имеет решение при любых значениях коэффициентов 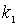 и 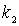 , т.е. при любых значениях энергии 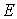 ( напомним, что 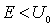 ). Это означает, что частица обладает непрерывным энергетическим спектром.
Найдем коэффициент отражения, определяющий вероятность того, что частица отразится от высокого порога. Согласно физическому смыслу, коэффициент отражения 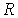 есть
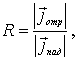 | (4.35) |
где 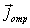 и 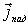 - векторы плотности потока вероятности соответственно для падающей (первое слагаемое в (4.34a)) и отраженной (второе слагаемое в (4.34a)) волн. Напомним, (см. (3.19)) , что вектор плотности потока вероятности определяется через волновую функцию следующим образом
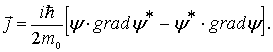 | (4.36) |
Подставляя эти выражения в (4.35), находим, что
Коэффициент прохождения частицы через порог 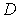 , определяющий вероятность того, что частица пройдет в область II (коэффициент прозрачности порога) , имеет вид
где 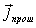 - вектор плотности потока вероятности для прошедшей волны 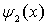 (4.34b) (4.34b). Подставляя 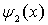 в (4.36) , получаем, что 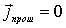 , а, следовательно и  .
Таким образом, в случае высокого порога
и выполняется условие:  .
Рассмотрим поведение частицы в области II высокого потенциального порога. Волновая функция частицы 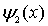 (см. (4.34b)) отлична от нуля и спадает с 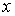 по экспоненциальному закону, а это означает, что существует отличная от нуля вероятность пребывания частицы под порогом, т.е. в области, в которой полная энергия частицы 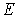 меньше ее потенциальной энергии 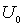 . С точки зрения классической механики эта область для частицы является запрещенной, т.к. условие 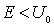 означает, что кинетическая энергия частицы должна быть отрицательной. Однако с точки зрения квантовой механики никакого противоречия здесь нет. Кинетическая энергия является функцией импульса частицы 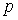 , а потенциальная энергия - функцией ее координаты 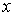 , но, согласно соотношению неопределенностей, одновременное точное определение координаты и импульса невозможно. Поэтому в квантовой механике представление полной энергии частицы в виде суммы одновременно точно определенных кинетической и потенциальной энергий, как уже отмечалось в разделе 2.3 , не имеет смысла.
Полученный результат означает, что микрочастицы могут проникать в области, которые для макроскопических частиц запрещены. Плотность вероятности нахождения частицы в области II определяется выражением
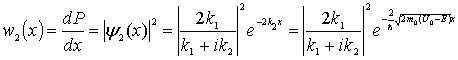 | (4.37) |
и зависит от массы частицы  , разности энергий 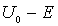 и расстояния от границы порога 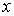 .
Оценим величину экспоненциального множителя в (4.37) для случая электрона, полагая 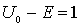 эВ . При  м , т.е. при расстоянии от порога, сравнимом с размерами атома,
Мы видим, что экспоненциальный множитель в этом случае имеет заметную величину, а это означает, что вероятность найти электрон на таком расстоянии в области II высокого потенциального порога достаточно велика. При 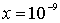 м
что означает, что вероятность пребывания электрона на таком расстоянии от порога ничтожно мала. Полученные оценки показывают, что электрон с заметной вероятностью может проникать в область II лишь на расстояния, сравнимые с размером атома.
Таким образом, хотя коэффициент отражения частицы от высокого барьера 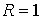 , т.е. отражение является полным, оно не обязательно происходит на самом пороге, т.е. на границе раздела областей I и II . С определенной вероятностью частица может проникнуть в область II и затем выйти из нее.
Интересно отметить, что рассмотренное явление имеет аналог в классической физике - явление полного внутреннего отражения в волновой оптике. В этом случае также происходит полное отражение при падении света на границу раздела оптически более плотной и оптически менее плотной сред. При этом свет может проникать в оптически менее плотную среду, однако его амплитуда, как и 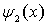 , убывает с глубиной по экспоненциальному закону.
Перейдем теперь к анализу случая, когда энергия налетающей на порог частицы 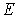 превышает высоту потенциального порога 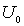 , т.е. 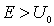 . Такой порог носит название низкого потенциального порога. В этом случае уравнение Шредингера для областей I и II имеет вид
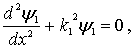 | (4.38a) |
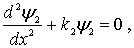 | (4.38b) |
где 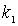 и 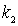 определяются соотношениями
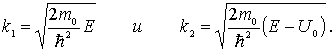 | (4.39) |
Решая уравнения (4.38) , получаем
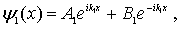 | (4.40a) |
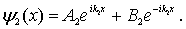 | (4.40b) |
Будем считать, что частица приближается к порогу со стороны отрицательных значений 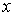 , т.е. движется слева направо. При этом первое слагаемое в 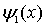 описывает падающую на порог волну де Бройля, а второе слагаемое в  - волну, отраженную от порога. Аналогично, первое слагаемое в 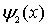 соответствует прошедшей через порог волне де Бройля. Поскольку отраженная волна в области II отсутствует, то коэффициент 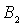 в (4.40b) следует положить равным нулю, т.е. 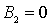 .
Условие сшивки волновых функций и их производных на границе ( при 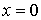 ) приводит к следующим уравнениям для коэффициентов 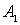 , 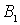 и 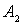
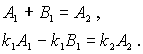 | (4.41) |
Полагая, как и в предыдущем случае 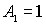 , для 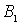 и 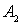 получаем
Таким образом, волновые функции частицы в случае ее движения в области низкого порога имеют вид
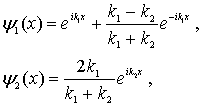 | (4.42) |
где 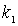 и 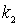 заданы соотношениями (4.39) .
Для того, чтобы найти коэффициенты отражения 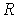 и прохождения 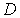 частицы через порог, найдем векторы плотности потока вероятности для падающей, отраженной и прошедшей (преломленной) волн де Бройля. Подставляя найденные волновые функции в (4.36), получаем
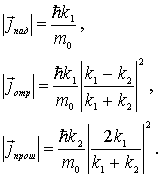 | (4.43) |
Коэффициент отражения частицы от низкого потенциального порога с учетом (4.35), (4.43) есть
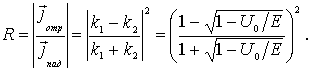 | (4.44) |
Из (4.44) следует, что при 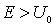 существует отличная от нуля вероятность отражения частицы от низкого потенциального порога, т.е. возможно так называемое надбарьерное отражение. Этот результат является чисто квантовым и объясняется наличием у частицы волновых свойств. Макроскопическая частица, подчиняющаяся законам классической механики, при прохождении через низкий потенциальный порог не испытывает отражения, в области порога лишь уменьшается ее кинетическая энергия.
Интересно отметить, что если потенциальный порог "обратить", т.е. считать, что 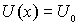 в области I и 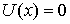 в области II , то коэффициент отражения 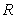 останется прежним. В этом случае изменится лишь разность фаз между падающей и отраженной волнами де Бройля. Так, в рассматриваемом случае знаки амплитуд падающей и отраженной волн (первое и второе слагаемое в 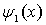 в выражении (4.42)) одинаковы, что соответствует разности фаз между волнами, равной нулю. В случае "обращенного" порога знаки амплитуд падающей и отраженной волн различны, что соответствует разности фаз, равной  . Т.е. при отражении от "обращенного" порога фаза волны скачком меняется на 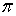 . Продолжая аналогию с оптикой, можно сказать, что область I является для волны де Бройля оптически более плотной, чем область II .
Коэффициент прохождения частицы через порог, согласно (4.37) , (4.44) , есть
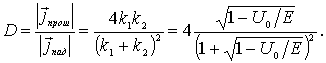 | (4.46) |
Таким образом, и в случае низкого порога 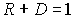 , что естественно было ожидать с точки зрения сложения вероятностей - падающая на порог частица либо отразится от него, либо пройдет в область II .
Следует отметить, что волна де Бройля, описывающая движение частицы в области порога, на границе раздела областей I и II испытывает преломление, связанное с изменением скорости частицы 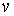 и ее волны де Бройля  . Показатель преломления 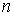 (см. раздел 2.1) имеет вид
где 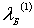 и 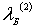 - дебройлевские длины волн, а 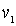 и  - скорости движения частицы соответственно в областях I и II . Выражая 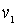 и 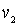 через кинетическую энергию частицы, получаем
В рассматриваемом случае низкого порога ( 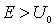 ) , показатель преломления 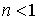 , что еще раз отражает тот факт, что область I является для частицы оптически более плотной средой, чем область II . В случае "обращенного" порога показатель преломления
оказывается больше единицы.
Прохождение частицы через потенциальный барьер. Область пространства, в которой потенциальная энергия частицы 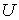 больше, чем в окружающих областях, называется потенциальным барьером. Анализ движения частицы в области потенциального барьера начнем с рассмотрения простейшего случая одномерного прямоугольного потенциального барьера (рис.4.8) . Пусть потенциальная энергия частицы имеет вид
Обозначим цифрой I область слева от барьера, цифрой II область 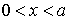 и цифрой III область справа от барьера. Будем считать, что
частица приближается к барьеру со стороны отрицательных значений  , т.е. движется слева направо. Рассмотрим случай, когда энергия частицы  меньше высоты потенциального барьера 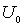 , т.е. 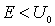 ( случай  рассмотрен в задаче 4.7 данного параграфа).
Уравнение Шредингера в областях I, II и III имеет вид
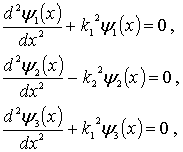 | (4.47) |
где 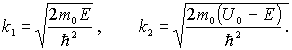
Волновые функции, являющиеся решением уравнений (4.47), есть
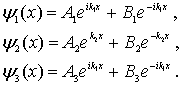 | (4.48) |
Как обычно, будем считать амплитуду падающей на барьер волны де Бройля 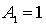 , а также положим коэффициент 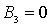 , принимая во внимание, что при движении частицы слева направо в области III может распространяться только проходящая волна.
Условие сшивки волновых функций и их производных на границах барьера, т.е. при 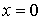 и 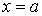 , приводят к следующей системе уравнений
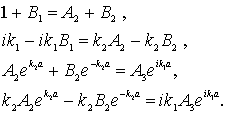 | (4.49) |
Система (4.49) представляет собой систему четырех уравнений с четырьмя неизвестными - коэффициентами 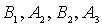 . Эта система имеет решение при любых значениях параметров 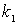 и 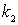 , т.е. при любых значениях энергии частицы 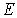 . Следовательно, энергетический спектр частицы является непрерывным.
Основное внимание в данной задаче сосредоточим на анализе прохождения частицы через барьер. Решая систему (4.49) , для амплитуды 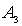 прошедшей через барьер волны получаем
Найдем вектор плотности потока вероятности для падающей на барьер и прошедшей через него волны. С учетом (4.36) , (4.48) получаем
Подставляя 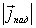 и 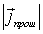 в (4.37) , находим коэффициент прохождения частицы через барьер
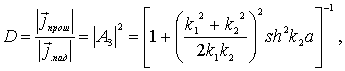 | (4.50) |
где гиперболический синус
В случае, когда ширина барьера 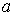 удовлетворяет условию 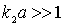 (приведенные выше численные оценки показывают, что для электрона это условие выполняется уже при ширине 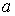 в несколько атомных слоев), 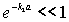 и гиперболический синус можно заменить экспонентой
Коэффициент прохождения частицы через порог 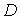 в этом случае принимает вид
Подставляя сюда выражения для 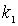 и 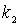 , получаем
Здесь коэффициент 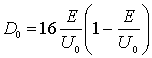 является медленно изменяющейся функцией отношения 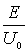 , численное значение которой по порядку величины сравнимо с единицей. Основной вклад в зависимость 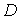 от параметров задачи дает экспонента. Поэтому в большинстве случаев при оценке коэффициента прохождения через потенциальный барьер полагают 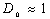 . При этом выражение для 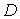 принимает вид
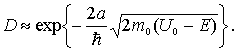 | (4.51) |
Из (4.51) следует, что коэффициент прохождения  испытывает сильную (экспоненциальную) зависимость от ширины барьера 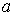 , массы частицы 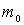 и разности энергий 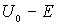 .
Обобщим полученный результат на случай потенциального барьера произвольной формы. Для этого представим потенциальный барьер в виде последовательности большого числа узких прямоугольных потенциальных барьеров, расположенных один за другим (рис.4.9а) . Будем считать, что
барьер имеет достаточно плавную форму, т.е. полагать, что его высота на расстоянии, сравнимом с длиной волны де Бройля, изменяется незначительно. В этом случае отражением волны на выступающих участках прямоугольных барьеров можно пренебречь и считать, что ослабление волны происходит в основном за счет поглощения.
Волна де Бройля, прошедшая через 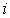 -ый прямоугольный барьер, представляет собой волну, падающую на 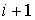 - ый барьер и т.д. Вероятность прохождения частицы через цепочку последовательно расположенных потенциальных барьеров равна произведению вероятностей прохождения через каждый из барьеров. Таким образом, коэффициент прохождения 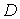 равен произведению коэффициентов прохождения 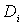 для каждого барьера
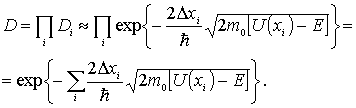 | (4.52) |
где 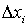 - ширина а 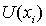 - высота 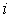 -го барьера. Переходя в (4.52) от суммирования к интегрированию, получаем
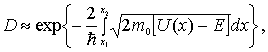 | (4.53) |
где 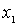 и 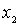 - значения координат, при которых  (рис.4.9б).
Туннельный эффект. Прохождение частицы через потенциальный барьер, высота которого превышает энергию частицы, получило название туннельного эффекта (частица, проходя под барьером, как бы движется в туннеле). Отметим, что туннельный эффект представляет собой чисто квантовое явление. Классическая частица, подходя к барьеру, высота которого больше ее полной энергии, отражается от него. Пройти через такой барьер, т.е. через область, в которой ее кинетическая энергия стала бы отрицательной, она не может. Квантовая частица может пройти через этот потенциальный барьер, причем вероятность ее прохождения испытывает сильную (экспоненциальную) зависимость от массы частицы, а также от вида потенциального барьера  . Подчеркнем, что при прохождении через барьер полная энергия частицы  не меняется.
Туннельный эффект объясняет ряд важных физических явлений, таких, например, как холодная эмиссия электронов из металла, радиоактивный  -распад ядер -распад ядер, контактную разность потенциалов и т.д. Кроме того, туннельный эффект находит очень широкое применение в технических приложениях. В частности, на его основе был создан сканирующий туннельный микроскоп (СТМ), который произвел подлинную революцию в физике и технике поверхности и имеет широкие перспективы в связи с развитием нанотехнологий.
Холодная эмиссия электронов из металла. Как известно, для того, чтобы вырвать электрон из металла, ему нужно сообщить дополнительную энергию, равную работе выхода 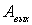 . Это означает, что электрон в металле находится в потенциальной яме, глубина которой 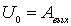
(рис.4.10а) . Пусть вблизи поверхности металла имеется электрическое
поле напряженности 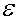 , способствующее выходу электронов из металла. Тогда вблизи поверхности металла потенциальная энергия электрона имеет вид
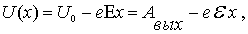 | (4.54) |
т.е. на границе металл-вакуум возникает потенциальный барьер треугольной формы ( рис.4.10б ) . Туннелирование электронов через этот барьер и объясняет явление холодной или, как ее еще называют, автоэлектронной эмиссии - выход электронов из металла при сколь угодно низких температурах.
Следует отметить, что для строгого решения данной задачи необходимо также принимать во внимание силу зеркального изображения, действующую со стороны металла на вылетевший электрон. Однако, учет этой силы, не оказывая заметного влияния на конечный результат, сильно усложняет вычисления. Поэтому вклад силы изображения в вид потенциального барьера мы здесь учитывать не будем.
В рамках классической физики явление холодной эмиссии не находит объяснения. Действительно, поскольку электрическое поле в металл не проникает, то оно может изменить потенциальную энергию электронов лишь вне металла. А это приводит к возникновению потенциального барьера, преодолеть который, согласно представлениям классической физики, электрон не может.
В квантово-механическом рассмотрении вероятность туннелирования электрона из металла определяется коэффициентом прохождения  через треугольный потенциальный барьер (рис.4.10б)
т.е. задача сводится к вычислению интеграла
где 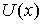 определено выражением (4.54) , а верхний предел интегрирования 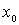 находится из условия 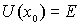 . Интегрируя, получаем
где величина 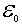 имеет смысл эффективного электрического поля в металле. Тогда коэффициент прохождения электронов через барьер принимает вид
Плотность тока холодной эмиссии 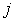 пропорциональна коэффициенту прохождения через барьер 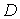 , следовательно плотность тока как функция напряженности электрического поля 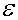 имеет следующий вид
Оценим величину 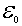 . Полагая 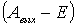 ~ 1 эВ, получаем
Это означает, что заметный по величине ток холодной эмиссии может достигаться лишь при приложении к металлу электрического поля, напряженность которого 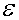 ~ 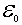 ~ 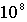 В/м .
Холодная эмиссия электронов находит широкое применение при изучении физических свойств поверхностей, адсорбции газов, явлений катализа и коррозии. Эмиттеры с холодной эмиссией (автоэлектронные эмиттеры) используются в технике, особенно в тех случаях, когда необходимо получить высокую плотность тока  . Для того, чтобы создать большую напряженность электрического поля  вблизи поверхности металла, автоэлектронные эмиттеры делают в виде поверхностей с малым радиусом кривизны: в виде острия, лезвия, торца нити и т.д.
На рис. 4.11 приведена электронная микрофотография эмиттера с многоострийной поверхностью, полученного отечественными учеными из Объединенного института ядерных исследований (г. Дубна) с помощью
современных трековых методик. Плотность острий эмиттера составляет ~ 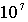 на квадратный сантиметр. По форме острия представляют собой конусы высотой 6,6 мкм и диаметром основания 1,5 мкм. Средний радиус кривизны вершины конусов составляет 0,1 мкм, угол раствора конуса 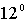 .
Важным достоинством эмиттеров с холодной эмиссией является то, что они не требуют энергетических затрат на подогрев, а также их безынерционность. В ряде случаев холодная эмиссия может играть и негативную роль, способствуя утечкам тока и развитию вакуумного пробоя. Для снижения влияния холодной эмиссии в таких ситуациях необходимо уменьшить поле 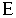 у поверхности проводника, или повысить работу выхода 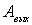 , подбирая соответствующие материалы или покрытия.
Радиоактивный 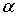 -распад. -распад. Еще одним важным примером прохождения частиц через потенциальный барьер является  -распад радиоактивных ядер. Он заключается в самопроизвольном испускании радиоактивным ядром  -частицы, т.е. ядра гелия, состоящего из двух протонов и двух нейтронов. Ядро, испускающее  -частицу, называется материнским ядром, после испускания оно превращается в дочернее ядро. Потенциальная энергия  -частицы в поле дочернего ядра представлена на рис. 4.12.
На больших расстояниях 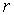 между 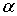 -частицей и ядром действуют силы кулоновского отталкивания и потенциальная энергия частицы имеет вид
где 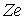 - заряд дочернего ядра, а 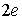 - заряд 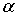 -частицы. Кулоновские силы между  -частицей и дочерним ядром действуют вплоть до расстояний, сравнимых с размерами ядра, и составляющих по порядку величины 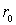 ~ 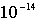 - 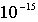 м . При 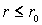 между  -частицей и ядром действуют более мощные силы - силы ядерного притяжения, которые значительно уменьшают потенциальную энергию частицы. Внутри ядра 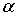 -частица находится в потенциальной яме, выйти из которой она может только за счет туннельного эффекта. Результаты расчета вероятности туннелирования не очень сильно зависят от формы ямы, так что яму можно считать прямоугольной и полагать, что ее ширина определяется радиусом ядра 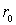 .
Результаты исследований показывают, что высота потенциального барьера при 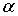 -распаде составляет величину порядка 20-30 МэВ, тогда как энергия испущенных 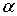 -частиц лежит в пределах 5-6 МэВ, т.е. оказывается существенно меньше высоты барьера. Это означает, что 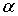 -частицы могут испускаться ядрами только за счет туннельного эффекта.
Как будет показано в разделе 7.2 , закон радиоактивного распада, определяющий изменение со временем числа нераспавшихся ядер, имеет вид
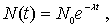 | (4.55) |
где 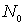 - число нераспавшихся ядер в начальный момент времени 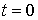 , а 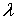 - величина, которая называется постоянной распада и характеризует скорость распада ядер.
Найдем связь между постоянной распада 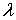 и коэффициентом прохождения 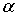 -частицы через потенциальный барьер 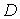 . Пусть радиус ядра равен 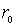 , а скорость  -частицы в ядре равна 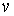 . Тогда число ударов 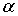 -частицы о стенки потенциального барьера в единицу времени равно 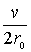 . Так как вероятность туннелирования при одном ударе о стенку равна 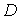 , а общее число ядер равно 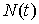 , то число ядер 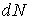 , в которых произойдет испускание 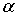 -частиц за время от момента 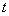 до момента 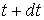 есть
Знак (-) в этом соотношении взят потому, что 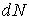 имеет смысл приращения числа нераспавшихся ядер, а их число на самом деле убывает.
С другой стороны, дифференцируя (4.55) по времени, получаем
Сравнивая эти два соотношения, находим, что
т.е. постоянная распада прямо пропорциональна коэффициенту прохождения через потенциальный барьер  .
Сканирующий туннельный микроскоп. Сканирующий туннельный микроскоп (СТМ) был создан в 1982 г сотрудниками исследовательского отдела фирмы IBM Г. Биннигом и Х. Рёрером. Он открыл очень многообещающие возможности научных и прикладных исследований в области нанотехники и явился первым техническим устройством, с помощью которого была осуществлена наглядная визуализация атомов и молекул. За создание СТМ Г. Бинниг и Х. Рёрер в 1986 году были удостоены Нобелевской премии по физике.
Принцип работы СТМ заключается в следующем: к поверхности проводящего образца на характерное межатомное расстояние  , составляющее доли нанометра, подводится очень тонкое металлическое острие (игла). При приложении между образцом и иглой разности потенциалов 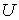 ~ 0,1  1 В в цепи (рис.4.13) появляется ток, обусловленный туннелированием электронов через зазор между ними.
Туннельный ток составляет ~ 1  10 нА , т.е. имеет величину, которую вполне можно измерить на эксперименте.
Поскольку вероятность туннелирования через потенциальный барьер экспоненциально зависит от ширины барьера (см. (4.51)), то туннельный ток при увеличении зазора между иглой и поверхностью образца 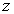 убывает по экспоненте и уменьшается примерно на порядок при увеличении 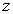 на каждые 0,1 нм. Экспоненциальная зависимость туннельного тока от расстояния обеспечивает чрезвычайно высокую разрешающую способность СТМ. Вдоль оси 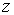 , перпендикулярной к поверхности образца, разрешающая способность СТМ составляет ~ 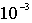 нм, а вдоль осей 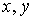 , параллельных поверхности образца, ~ 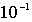 нм. Перемещая иглу СТМ вдоль поверхности образца, т.е. осуществляя сканирование поверхности, можно получать информацию о рельефе поверхности с атомным пространственным разрешением.
Существуют два варианта режима работы СТМ : режим постоянной высоты и режим постоянного тока. При работе в режиме постоянной высоты острие иглы перемещается в горизонтальной плоскости над исследуемой поверхностью ( рис.4.14а ). Туннельный ток при этом изменяется и по этим изменениям легко может быть определен рельеф поверхности образца.
При работе в режиме постоянного тока ( рис.4.14б ) используется система обратной связи, которая поддерживает постоянным туннельный ток за счет перемещения острия иглы в вертикальном направлении. В этом случае информация о рельефе поверхности получается на основании данных о перемещении иглы.
Общая схема СТМ приведена на рис. 4.15. С помощью системы грубого подвода и позиционирования игла СТМ подводится к исследуемой поверхности на расстояние ~ 0,1 мкм . Дальнейшее перемещение иглы и исследование поверхности проводится с помощью
специального сканирующего устройства. Это устройство изготовлено из пьезоэлектрика, т.е. вещества, способного изменять свои линейные размеры при приложении к нему электрического поля, и позволяет перемещать иглу СТМ над поверхностью образца с очень высокой точностью.
Одним из наиболее важных узлов СТМ является игла (острие), в качестве которой используется тонкая проволока из вольфрама, ванадия или другого проводящего материала. Для улучшения характеристик кончика острия его подвергают электрохимическому травлению. Эксперименты показывают, что травление острия с радиусом кончика 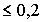 мкм практически обеспечивает разрешение на атомном уровне.
Управление движением сканирующего устройства и контроль за работой системы обратной связи осуществляется компьютером. С его помощью проводится запись результатов измерения, их обработка и визуализация исследуемой поверхности. Типичные результаты исследований, выполненные с помощью СТМ , приведены на рис. 4.16, на
котором представлены изображения молекул 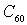 , адсорбированных на поверхности кристалла меди. Размеры по осям  и  приведены в ангстремах ( 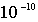 м).
Важно отметить, что СТМ, в отличие от других электронных микроскопов, не содержит линз и, следовательно, получаемое в нем изображение не искажается из-за аберраций. Кроме того, энергия электронов, формирующих изображение в СТМ, не превышает нескольких электронвольт, т.е. оказывается меньше характерной энергии химической связи, что обеспечивает возможность неразрушающего контроля исследуемого образца. Напомним, что в электронной микроскопии высокого разрешения (см. раздел 2.4) энергия электронов достигает сотен килоэлектронвольт, что приводит к образованию радиационных дефектов.
В настоящее время перспективны следующие области применения СТМ:
Физика и химия поверхности на атомном уровне.
Нанометрия - исследование с нанометровым разрешением шероховатости поверхности, процессов зародышеобразования при росте пленок, процессов химического или ионного травления, осаждения и т.д.
Нанотехнология - исследование и изготовление приборных структур нанометрового размера.
Исследование макромолекул, вирусов и других биологических структур.
Подводя итог описанию СТМ, следует отметить, что его возможности выходят далеко за рамки чисто микроскопических задач. С его помощью, например, можно заставить атомы перемещаться вдоль поверхности и собирать из них искусственные структуры нанометровых размеров. Так, в частности, с помощью острия сканирующего туннельного микроскопа из атомов инертного газа ксенона, "рассыпанных" на поверхности никеля, была собрана аббревиатура фирмы IBM ( рис.4.17 ). Такие возможности СТМ делают его перспективным инструментом при разработке и создании нанотехники будущего поколения, например, квантового компьютера. Сканирующий туннельный микроскоп явился прототипом целого семейства более совершенных сканирующих микроскопов. На базе СТМ был создан сканирующий атомно-силовой микроскоп (АСМ), который
позволяет исследовать непроводящие вещества, микроскоп на магнитных силах, дающий возможность изучать магнитные свойства поверхности и т.д.
Все сказанное выше о СТМ позволяет сделать следующее заключение: "Принцип действия СТМ настолько прост, а потенциальные возможности так велики, что невозможно предсказать его воздействие на науку и технику даже ближайшего будущего".
Задача 4.6. Частица массы 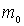 падает слева на прямоугольный потенциальный порог высоты 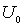 . Энергия частицы равна 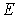 , причем 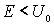 . Найдите эффективную глубину 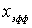 проникновения частицы в область порога. Вычислите 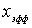 для электрона, если 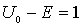 эВ .
Решение: Поскольку, согласно условию задачи, энергия частицы 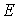 меньше высоты порога 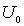 , то мы имеем дело с высоким потенциальным порогом (рис.4.7). В этом случае, как уже отмечалось выше, хотя коэффициент отражения частицы от порога равен единице, тем не менее существует вероятность обнаружить частицу в области под порогом, т.е. при 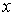 > 0 . Согласно (4.37) плотность вероятности нахождения частицы в области под порогом имеет вид
где 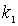 и 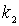 определяются выражениями (4.29) . Определим эффективную глубину проникновения частицы 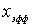 в область потенциального порога как расстояние от границы порога, на котором плотность вероятности обнаружения частицы уменьшается в  раз. Из этого определения следует, что
В случае электрона, налетающего на потенциальный порог, для которого 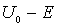 = 1 эВ , получаем
Задача 4.7. Частица массы 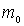 падает на прямоугольный потенциальный барьер высоты 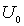 и ширины 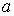 . Энергия частицы 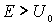 . Найдите: а) коэффициент прозрачности барьера  ; б) значения энергии частицы, при которых она будет беспрепятственно проходить через такой барьер.
Решение: Обозначим цифрой I область  меньше 0 , цифрой II область 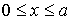 , и цифрой III область 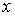 > 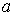 . Решения уравнения Шредингера в этих трех областях имеют вид
где 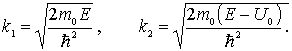
Условие сшивки волновых функций и их производных на границах барьера (при 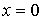 и 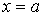 ) приводят к следующей системе уравнений
Решая эту систему, находим амплитуду прошедшей волны
Коэффициент прохождения частицы над потенциальным барьером 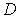 выражается через векторы плотности потока вероятности для падающей и прошедшей волн
В данном случае 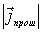 = 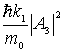 , 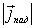 = 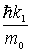 , следовательно
Подставляя сюда выражения для 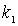 и 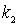 , получаем
Коэффициент прохождения 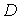 обращается в единицу при 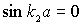 , т.е. при
Таким образом, значения энергии частицы, при которых 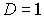 , равны
Следует подчеркнуть, что хотя значение  формально и удовлетворяет условию 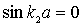 , но при 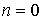 коэффициент прохождения 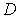 не будет равен единице. Дело в том, что при  энергия частицы 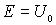 , т.е. 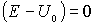 и параметр 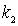 также равен нулю. Это означает, что числитель и знаменатель дроби в выражении для 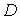 равны нулю. Избавляясь от неопределенности, находим, что коэффициент прохождения при 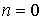 оказывается равным
Отметим, что аналогичным образом решается задача о движении частицы над прямоугольной потенциальной ямой конечной глубины.
|