3.8. Матричная форма квантовой механики
Представление физических величин эрмитовыми операторами, действующими на волновую функцию, не является единственно возможным математическим аппаратом квантовой механики. В 1925 г. еще до открытия Э.Шредингером основного уравнения для волновой функции, В.Гейзенберг предложил в квантовой механике каждой физической величине ставить в соответствие некоторую матрицу с бесконечным числом строк и столбцов.
Такая "матричная" форма квантовой механики была развита в работах В.Гейзенберга, М.Борна, П.Иордана и других физиков параллельно, а на первом этапе даже независимо от волновой теории с использованием операторов. И только позже Э.Шредингер показал, что представления физических величин операторами и матрицами эквивалентны, хотя математический аппарат этих двух методов решения задач квантовой механики оказывается различным.
Связь между операторами и матрицами физических величин установим, считая для упрощения выкладок, что спектры рассматриваемых квантовомеханических операторов являются дискретными, хотя все обсуждаемые ниже соотношения были обобщены Дираком и на случай операторов с непрерывными спектрами.
Пусть 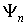 , 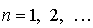 - известный набор собственных функций некоторого квантовомеханического оператора 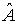 . Из свойств собственных функций эрмитовых операторов следует, что любую регулярную функцию 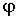 можно разложить в ряд по собственным функциям оператора:
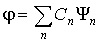 , , | (3.85) |
причем коэффициенты этого разложения определяются по формулам
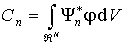 . . | (3.86) |
Если теперь в качестве функции 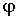 взять функцию 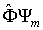 , являющуюся результатом действия на функцию  оператора  физической величины 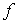 , то из (3.85) и (3.86) следует равенство
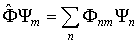 , , | (3.87) |
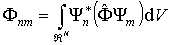 . . | (3.88) |
Величины 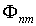 можно рассматривать как элементы некоторой бесконечной матрицы
 .
Эту матрицу называют матрицей оператора 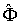 (или физической величины 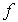 ) в системе собственных функций оператора 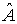 , или, как говорят, в 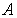 - представлении. В квантовой механике при этом используются координатное, импульсное, энергетическое и другие представления.
Каждую величину 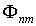 называют матричным элементом, соответствующим переходу из состояния  в состояние 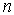 . Матричный элемент имеет два индекса. Первый 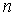 - есть номер строки, а второй 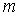 - номер столбца матрицы.
Для матричных элементов 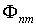 применяется также обозначение, предложенное Дираком,
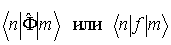 . . | (3.89) |
Такой символ можно рассматривать как сконструированный из обозначения физической величины  (или соответствующего ей оператора 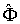 ) и символов 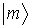 и 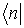 . Формально, каждую собственную функцию 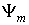 (начальное состояние) представляет некоторый базисный вектор 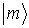 бесконечномерного пространства, который называют кет-вектором. Собственную функцию  (конечное состояние) представляет вектор 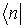 , который называют бра-вектором. Такие названия происходят от английских  и  , образующих слово  (скобка).
Заметим, что обозначение 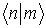 следует рассматривать как сокращенную запись выражения 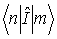 , где 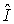 - единичный (тождественный) оператор, для которого  . Поэтому
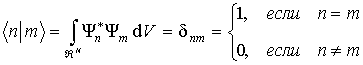 .
Итак, оператор  физической величины 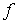 в 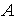 -представлении определяется матрицей 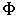 , элементы которой 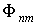 определяются соотношением (3.88). При этом эрмитову оператору всегда соответствует эрмитова матрица, для матричных элементов которой справедливо соотношение 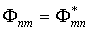 .
Определим некоторые алгебраические операции над матрицами Гейзенберга:
1. Сложение матриц. Если 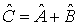 , то для матричных элементов матрицы  выполняется равенство
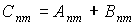 .
2. Умножение матриц. Если 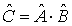 , то матричные элементы матрицы 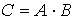 определяются по правилу перемножения матриц
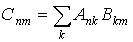 .
При этом произведение матриц, как и произведение операторов, не коммутативно, то есть в общем случае 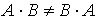 .
3. Так как правила сложения и умножения матриц определены, то можно определить простейшие функции матриц. Так например, под функцией 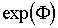 будем понимать следующий ряд из матриц
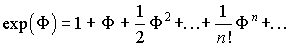 .
Отметим одно важное свойство матриц Гейзенберга физических величин в квантовой механике. Если определить матричные элементы 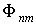 оператора 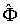 в собственном  - представлении, когда 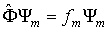 , то из (3.88) получаем
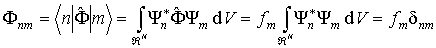 .
Это означает, что матрица оператора 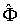 в собственном представлении является диагональной матрицей, то есть матрицей, у которой отличны от нуля лишь элементы с 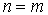 , причем эти диагональные элементы являются собственными значениями оператора 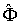 .
Таким образом, важная задача квантовой механики об определении собственных значений квантовомеханического оператора  в матричной формулировке сводится к нахождению такого преобразования матрицы, которое приводит ее к диагональному виду.
Представление квантовой механики в матричной форме позволяет формулировать уравнения квантовой механики так, что в них не фигурирует волновая функция, а сами уравнения по форме совпадают с уравнениями классической механики, но с тем принципиальным отличием, что в этих уравнениях классические физические величины заменены соответствующими матрицами.
В некоторых случаях при решении задач квантовой механики матричная форма оказывается даже удобнее операторной. Но в нашем курсе при решении задач квантовой механики мы будем использовать только операторную форму квантовой механики с использованием волновой функции и волнового уравнения Шредингера. Примеры решения некоторых задач квантовой механики в матричной форме можно найти в учебниках по теоретической физике.
|