3.2. Уравнение Шредингера
Как, зная структуру силового поля, в котором движется частица, определить волновую функцию, описывающую квантовомеханическое состояние этой частицы? Как, зная волновую функцию в начальный момент времени, описать эволюцию волновой функции во времени? Ответы на эти вопросы дает основное уравнение нерелятивистской квантовой механики, сформулированное Э.Шредингером в 1926 г.
Общее временное уравнение Шредингера, позволяющее определить в любой момент времени волновую функцию 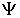 для частицы массы 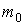 , движущейся в силовом поле 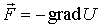 , описываемом скалярной потенциальной функцией 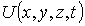 , имеет вид
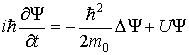 . . | (3.8) |
Здесь 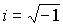 - мнимая единица, а 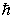 - рационализированная постоянная Планка. Стандартным символом 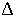 в (3.8) обозначен дифференциальный оператор Лапласа, который в декартовой системе координат имеет вид
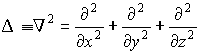 . . | (3.9) |
В общем случае в задачах квантовой механики дифференциальное уравнение в частных производных (3.8) должно решаться с учетом определенных начальных и граничных условий на волновую функцию.
Начальное условие задает значение волновой функции в начальный момент времени 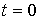 .
Граничные условия являются следствием регулярности волновой функции, обеспечивая, в частности, ее непрерывность. Эти условия формулируются на границах областей, где потенциальная функция 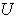 терпит разрывы первого или второго рода. Сюда же относятся условия на волновую функцию в бесконечно удаленных точках пространства, которые обеспечивают выполнение условия нормировки (3.4).
Уравнение Шредингера, как и законы классической механики Ньютона, законы термодинамики, уравнения электродинамики Максвелла и другие основные физические уравнения, не может быть выведено из других соотношений. Его следует рассматривать как некоторое научное положение, справедливость которого доказывается согласием результатов расчетов, выполненных с помощью уравнения Шредингера, с данными экспериментов. Такое согласие установлено для большого числа явлений в атомной и ядерной физике. Квантовые эффекты, предсказанные с помощью уравнения Шредингера, лежат в основе многих технических устройств, приборов и технологий.
Уравнение Шредингера тесно связано с гипотезой де Бройля и вытекающим из неё корпускулярно-волновым дуализмом материи. Действительно, непосредственной проверкой легко убедиться, что для свободной частицы, с кинетической энергий 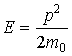 , движущейся в отсутствие силовых полей ( 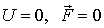 ) в направлении оси 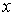 , решением соответствующего уравнения Шредингера
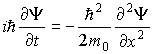 | (3.10) |
является волновая функция
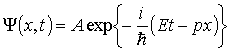 , , | (3.11) |
соответствующая плоской волне де Бройля. Этот факт позволяет утверждать, что и в общем случае уравнение Шредингера является волновым уравнением. Линейность этого уравнения обуславливает принцип суперпозиции квантовых состояний, физическое содержание которого обсуждалось в предыдущем параграфе.
Как уже указывалось, квантовая механика содержит в себе классическую механику как некоторый предельный случай. Значит, соответствующий предельный переход можно осуществить и в основном уравнении квантовой механики. Уравнение Шредингера после такого предельного преобразования должно перейти в основное уравнение классической механики.
Связь между квантовой и классической механикой аналогична связи между волновой и геометрической оптикой. В обоих случаях переход от одной теории к другой соответствует переходу от относительно больших длин волн (частицы или излучения) к малым длинам волн, если их сравнивать с характерным размером 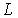 области неоднородности силового поля или оптических свойств среды. Этот вывод иллюстрирует следующая таблица
Волновая оптика | Квантовая механика |
| |
Геометрическая оптика | Классическая механика |
| |
В таком сравнении теорий траектория движения классической частицы является аналогом светового луча в геометрической оптике.
Формально, малость длины волны де Бройля для частицы можно обеспечить, считая квант действия 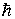 некоторым параметром задачи и осуществляя предельный переход 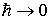 по этому параметру. Действительно, по формуле де Бройля (2.2) при 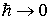 длина волны де Бройля также стремится к нулю. Поэтому переход от квантовой теории к классической в уравнении Шредингера (3.8) можно осуществить, выполняя в нем предельный переход 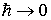 . В курсах теоретической физики анализируются результаты такого предельного перехода и доказывается, что при 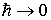 общее временное уравнение Шредингера (3.8) переходит в уравнение Гамильтона-Якоби классической механики.
Следует отметить, что с помощью волновых функций, найденных из решений уравнения Шредингера, можно описывать квантовые состояния только нерелятивистских частиц, которые движутся со скоростями, много меньшими скорости света в вакууме. Переход к релятивистским скоростям частиц в квантовой механике был впервые осуществлен для электрона П.Дираком в 1928 г. Такой переход потребовал принципиально новых физических идей для описания квантовых состояний релятивистских частиц, результатом применения которых явилось создание релятивистской квантовой механики. В основе этой теории лежит уравнение Дирака, которое обобщает уравнение Шредингера и в настоящее время широко используется в квантовой электродинамике и теории элементарных частиц.
|