3.1. Волновая функция
Особенности описания движения частиц в квантовой механике. Согласно гипотезе де Бройля, движущаяся частица обладает волновыми свойствами, и этими свойствами нельзя пренебречь, если длина волны де Бройля частицы 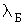 сравнима или больше характерного размера 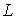 области движения частицы. Как показывают оценки, условие 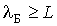 выполняется для частиц малых масс, движущихся в областях, размеры которых сравнимы с размерами атомов. Такие частицы в дальнейшем будем называть микрочастицами.
Для описания движения микрочастицы, обладающей волновыми свойствами, не может быть использован способ, разработанный в классической механике, когда состояние частицы определяется заданием в любой момент времени ее пространственных координат и скорости (импульса). При этом движение частицы связано с изменением со временем ее механического состояния, а непрерывная смена состояний соответствует движению частицы по определенной траектории.
Наличие у микрочастицы волновых свойств, как это следует из соотношений неопределенностей Гейзенберга (2.16), делает невозможным одновременное точное определение координат и импульса микрочастицы. Следовательно, механическое состояние микрочастицы не может быть задано классическим способом, а представление о траектории движения микрочастицы принципиально не может быть использовано для описания ее движения.
Такой отказ от традиционного классического способа описания движения частицы может даже вызвать внутренний протест. Как это частица может двигаться в пространстве, не имея при этом траектории движения? Вероятно, мы просто не можем измерить ряд параметров, знание которых позволило бы описать траекторию, по которой все таки движется частица. Еще раз подчеркнем, что это не так. История развития физики показала, что только отказавшись от классического способа описания движения частицы, только отказавшись от представления о траектории движения, можно правильно и полно описать движение микрочастицы, обладающей волновыми свойствами, и предсказать результаты экспериментов с такими частицами.
Физическая теория, в которой описывается движение частиц, обладающих волновыми свойствами, первоначально получила название волновой механики. Однако, это название вскоре было заменено другим названием - квантовая механика - так как оказалось, что волновая механика предсказывает дискретный характер, то есть квантование различных физических величин у движущихся микрочастиц. Именно название квантовая механика закрепилось за этой теорией.
Квантовая механика является более общей физической теорией, чем классическая механика. Однако, при выполнении условия 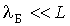 , когда волновыми свойствами частицы можно пренебречь, выводы квантовой механики должны совпадать с результатами классической механики. Этого требует принцип соответствия, утверждающий, что любая более общая физическая теория не должна исключать предыдущую, а должна включать ее как предельный частный случай. Поэтому при описании движения ракеты в космическом пространстве, подводной лодки в глубинах океана и даже при описании движения электрона в электронно-лучевой трубке физика всегда с успехом будет использовать классический способ описания механического движения тел. Только при существенном уменьшении пространственных масштабов движений микрочастиц, с которыми имеет дело атомная и ядерная физика, а также физика элементарных частиц, квантовая механика становится единственно возможным аппаратом описания явлений микромира. Отметим однако, что хотя квантовые эффекты проявляются на уровне атомных систем, эти эффекты определяют особенности работы многих современных установок и приборов и лежат в основе передовых технологий.
Переходя к описанию движения частиц в квантовой механике, сформулируем ряд ее постулатов, лежащих в основе теории.
Первый постулат квантовой механики: Состояние частицы в квантовой механике описывается заданием волновой функции 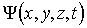 , являющейся функцией пространственных координат и времени. , являющейся функцией пространственных координат и времени.
Аппарат, разработанный в квантовой механике, позволяет, проводя некоторые операции над волновой функцией 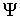 , получать полную информацию о движении микрочастицы.
Вероятностный смысл волновой функции. Невозможность задания состояния микрочастицы указанием в любой момент времени ее координат и скорости и отказ от траекторного способа описания движения приводит к вероятностному способу описания движения микрочастицы. Это означает, что в квантовой механике, определяя состояние частицы, следует указать способ определения вероятности обнаружения частицы в различных точках пространства в данный момент времени.
В 1926 г. М.Борн так сформулировал вероятностный смысл волновой функции в квантовой механике:
Квадрат модуля волновой функции 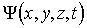 определяет плотность вероятности определяет плотность вероятности 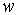 того, что в момент времени того, что в момент времени 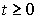 частица может быть обнаружена в точке пространства частица может быть обнаружена в точке пространства 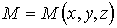 с координатами с координатами 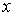 , , 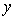 и и 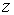 . .
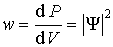 . . | (3.1) |
Отметим, что волновая функция в общем случае является комплекснозначной функцией, то есть содержит действительную и мнимую части. Физический смысл, поэтому, имеет не сама волновая функция, а ее квадрат модуля 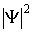 - действительная величина, которую во многих случаях удобно находить, умножая волновую функцию 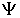 на комплексно сопряженную ей функцию 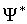 , так как из теории комплексных чисел следует, что 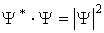 .
Преобразуем формулу (3.1) к виду
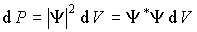 . . | (3.2) |
Здесь 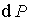 - вероятность того, что для заданного квантового состояния частицы в некоторый момент времени мы обнаружим частицу в элементарном объеме 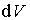 , окружающем точку 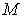 (рис. 3.1).
При описании движения частиц мы будем использовать 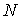 - мерное ( 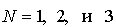 ) евклидово пространство 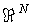 . Обычно, в этом пространстве, которое в физике называют конфигурационным пространством, вводят декартову прямоугольную систему координат. В такой системе координат для одномерного ( 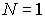 ) движения частицы вдоль оси 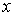 элемент "объема" 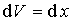 , для двумерного движения на плоскости ( 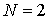 ) 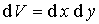 , а для трехмерного движения ( 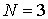 ) 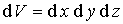 . В задачах, обладающих пространственными симметриями, можно использовать также цилиндрическую 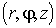 или сферическую 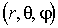 системы координат, определяя волновую функцию как функцию этих координат и времени.
Из формулы (3.2) следует, что в заданном квантовом состоянии частицы, описываемом волновой функцией 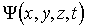 , можно рассчитать также вероятность 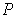 того, что частица будет обнаружена в любой области пространства конечного объема 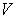 . Действительно, так как
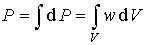 ,
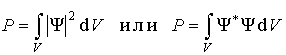 . . | (3.3) |
Формулы (3.1) - (3.3) определяют вероятностный или статистический смысл волновой функции в квантовой механике.
Свойства волновой функции. Если в качестве области пространства в (3.3) взять все пространство 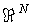 , для которого 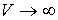 , то обнаружение частицы во всем пространстве является достоверным событием, вероятность которого равна единице. Следовательно, из вероятностного смысла волновой функции вытекает, что
 . . | (3.4) |
Условие (3.4) называют условием нормировки волновой функции, а волновую функцию, удовлетворяющую этому условию, называют нормированной волновой функцией.
Следует заметить, что в некоторых задачах квантовой механики условие нормировки в виде (3.4) может не выполняться. В таких задачах частица движется из бесконечности и уходит в бесконечность. Поэтому квадрат модуля волновой функции в таких задачах не стремится к нулю на бесконечности, и интеграл в условии (3.4) становится расходящимся. Примером такой волновой функции служит плоская волна де Бройля (2.3), которая является волновой функцией, описывающей квантовое состояние свободно движущейся частицы. При использовании ненормированных волновых функций важно не абсолютное значение квадрата модуля волновой функции, а отношение ее квадратов модулей в двух точках пространства. Это отношение определяет отношение вероятностей обнаружения частицы вблизи этих точек пространства. Следует отметить, что в задачах с ненормированными волновыми функциями некоторый аналог условия нормировки может быть получен с использованием плотности потока вероятности. Определение этой физической величины и связь ее с волновой функцией будут даны в параграфе 3.3.
Вероятностный смысл волновой функции накладывает определенные ограничения или условия на волновые функции в задачах квантовой механики. Эти стандартные условия часто называют условиями регулярности волновой функции. Они включают в себя:
1. Условие конечности волновой функции. Волновая функция не может принимать бесконечных значений, таких, что интегралы в (3.3) и (3.4) станут расходящимися интегралами. Таким образом, это условие требует, чтобы волновая функция была квадратично интегрируемой функцией. В частности, в задачах с нормированной волновой функцией квадрат модуля волновой функции должен стремиться к нулю на бесконечности.
2. Условие однозначности волновой функции. Волновая функция должна быть однозначной функцией координат и времени, так как плотность вероятности обнаружения частицы должна определяться в каждой задаче однозначно. В задачах с использованием цилиндрической или сферической системы координат условие однозначности приводит к периодичности волновых функций по угловым переменным.
3. Условие непрерывности волновой функции. В любой момент времени волновая функция должна быть непрерывной функцией пространственных координат. Кроме того, непрерывными должны быть также частные производные волновой функции
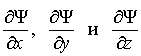 .
Эти частные производные волновой функции лишь в редких случаях задач с идеализированными силовыми полями могут терпеть разрыв в тех точках пространства, где потенциальная функция, описывающая силовое поле, в котором движется частица, испытывает разрыв второго рода.
Принцип суперпозиции квантовых состояний. Сформулируем одно из важных свойств квантовых состояний, которое формально является следствием линейности уравнения Шредингера для волновой функции, которое будет обсуждаться в следующем параграфе. Из линейности этого уравнения следует, что если частица может находиться в квантовом состоянии, описываемом волновой функцией 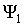 , а также в другом квантовом состоянии, описываемом волновой функцией , а также в другом квантовом состоянии, описываемом волновой функцией 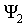 , то эта частица может также находиться в состоянии, описываемом волновой функцией , то эта частица может также находиться в состоянии, описываемом волновой функцией
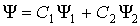 , , | (3.5) |
где 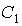 и и 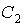 , в общем случае комплексные числа , в общем случае комплексные числа.
Очевидно, можно говорить и о суперпозиции (сложении) любого числа квантовых состояний, то есть о существовании квантового состояния частицы, которое описывается волновой функцией
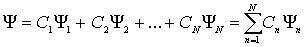 . . | (3.6) |
В таком состоянии квадрат модуля коэффициента 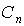 определяет вероятность того, что при измерении, проведенном над системой с такой волновой функцией 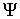 , мы обнаружим ее в квантовом состоянии, описываемом волновой функцией 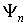 . Поэтому для нормированных волновых функций 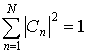 .
Квантовомеханический принцип суперпозиции состояний не имеет аналога в классической механике. Действительно, в классической теории свободная частица в данный момент времени движется либо в одном направлении в пространстве, либо в другом направлении.
А куда движется квантовая частица, состояние которой описывается волновой функцией, являющейся суперпозицией двух плоских волн де Бройля
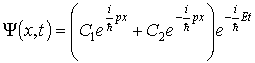 .
Такая частица одновременно движется и вправо вдоль оси 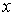 и влево. С точки зрения классической механики такой ответ абсурден. С позиций квантовой механики это означает, что при проведении серии опытов по обнаружению направления движения частицы, находящейся в таком квантовом состоянии, с вероятностью 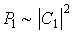 будет получен ответ, что частица движется вправо вдоль оси 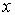 , а с вероятностью 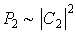 - что частица движется влево.
Точно также в состоянии, являющемся суперпозицией двух плоских волн де Бройля, распространяющихся в направлениях вдоль осей 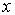 и 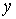 , когда
нет однозначного ответа на вопрос "куда движется частица?". Ответ, что частица движется и в направлении оси 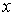 и в направлении оси 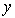 не означает, что она движется вдоль биссектрисы угла между осями 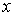 и 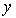 . Такой ответ означает, что это движение, в котором следует считать, что частица с некоторой вероятностью движется вдоль оси 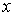 , а с некоторой вероятностью - вдоль оси 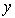 . Такой результат будет получен в серии измерений направления движения частицы.
Столь необычный ответ квантовой механики казалось бы на простой вопрос, не является чисто теоретическим абстрактным результатом. В связи с этим отметим, например, что в современных информационных технологиях, разрабатывающих квантовые компьютеры, возможно использование логического элемента не только с двумя состояниями "0" и "1", но и элементов, которые могут находиться в состояниях суперпозиции нуля и единицы с некоторыми вероятностями. Такие элементы существенно изменяют принцип работы компьютера и позволяют создавать алгоритмы, значительно повышающие быстродействие и эффективность переработки информации.
Возможность состояний, в которых данная физическая величина не имеет определенного значения, и которые получаются суперпозицией состояний, с определенным значением этой величины, является характерной чертой квантовой механики, принципиально отличающей ее от классической механики. Описать такое "смешанное" состояние одной частицы на языке классической механики невозможно. Поэтому не следует рассматривать системы, в которых формально объединены как классические, так и квантовые объекты. Такие системы некорректны для исследования, так как в них обнаруживаются неразрешимые противоречия. Одно из таких противоречий демонстрирует предложенный Э.Шредингером парадокс, который получил название " парадокса кошки".
Пусть в замкнутой системе, которая изображена на рис. 3.2 и ограничена некоторым непроницаемым "ящиком", находится кошка. На кошку направлен ствол заряженного пулей ружья. Перед нами система, содержащая классические объекты. Запустим теперь в этот ящик движущуюся микрочастицу, обладающую волновыми свойствами. При попадании этой квантовой частицы в курок ружья, ружье стреляет, и кошка погибает.
Пусть наша частица может находиться в первом квантовом состоянии, описываемом волновой функцией 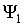 , и пусть в этом состоянии вероятность обнаружить частицу в области вблизи курка равна нулю. Это означает, что если микрочастица находится в первом квантовом состоянии, то кошка в ящике жива.
Есть другое состояние частицы, описываемое волновой функцией 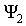 . В этом квантовом состоянии вероятность нахождения частицы в области вблизи курка ружья велика и практически равна единице. Неудивительно, что если частица находится во втором состоянии, то кошка мертва.
По принципу суперпозиции состояний микрочастица может находиться и в состоянии, которое является суперпозицией первого и второго состояний и описывается волновой функцией
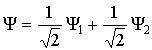 . . | (3.7) |
Тот факт, что частица в таком состоянии с равной вероятностью может быть обнаружена либо в состоянии 1, либо в состоянии 2, возражений не вызывает. Однако, естественно, возникает коварный вопрос. Жива или мертва кошка в состоянии микрочастицы, описываемом волновой функцией (3.7)? Ведь кошка не может находиться в состоянии, которое является суперпозицией жизни и смерти, то есть не может быть не живой, не мертвой. Так жива или мертва кошка? Ведь если мы откроем ящик, то однозначно увидим, что кошка или жива, или мертва. И если она мертва, то когда это произошло? Ведь до открытия ящика однозначного ответа, что кошка мертва, не могло быть. Неужели мы убили кошку тем, что открыли ящик? На все поставленные вопросы нет ответов только потому, что была рассмотрена некорректная система, которая формально объединяла классические и квантовые объекты.
Задача 3.1. Волновая функция, описывающая состояние микрочастицы, движущейся в сферически симметричном силовом поле с расстоянием 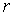 от центра, имеет вид от центра, имеет вид
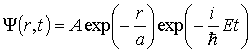 .
Здесь 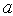 - известная постоянная, а - известная постоянная, а 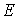 - полная энергия частицы, не зависящая от времени. - полная энергия частицы, не зависящая от времени.
Определите: а) значение постоянного множителя 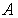 ; б) наиболее вероятное расстояние частицы от силового центра. ; б) наиболее вероятное расстояние частицы от силового центра.
Решение: а) Значение постоянной 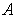 найдем из условия нормировки волновой функции (3.4), выбирая в качестве элементарного объема объем шарового слоя радиусов от найдем из условия нормировки волновой функции (3.4), выбирая в качестве элементарного объема объем шарового слоя радиусов от 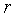 до до 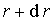 . Объем такого слоя . Объем такого слоя 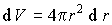 . Условие нормировки приводит к соотношению . Условие нормировки приводит к соотношению
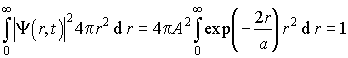 .
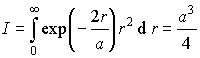 ,
из условия нормировки находим
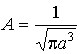 .
б) Наиболее вероятное расстояние частицы от силового центра найдем, записав вероятность нахождения частицы на расстоянии 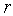 от центра, точнее, в выделенном шаровом слое. Эта вероятность равна от центра, точнее, в выделенном шаровом слое. Эта вероятность равна
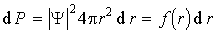 ,
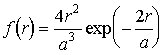 .
Приравняв производную 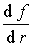 нулю, находим экстремальную точку нулю, находим экстремальную точку 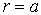 , где функция , где функция 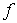 достигает максимума. Именно на расстоянии достигает максимума. Именно на расстоянии 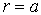 от силового центра в заданном квантовом состоянии наиболее вероятно обнаружить частицу. Это расстояние со временем не изменяется. от силового центра в заданном квантовом состоянии наиболее вероятно обнаружить частицу. Это расстояние со временем не изменяется.
Задача 3.2. В момент времени 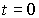 волновая функция, описывающая квантовое состояние частицы, движущейся вдоль оси волновая функция, описывающая квантовое состояние частицы, движущейся вдоль оси 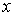 , имеет вид , имеет вид
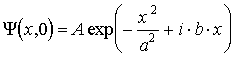 ,
где 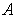 , , 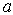 и и 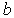 - известные действительные константы. - известные действительные константы.
Определите зависимости от координаты 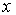 : а) действительной части волновой функции; б) квадрата модуля волновой функции. : а) действительной части волновой функции; б) квадрата модуля волновой функции.
Решение: а) Найдем действительную часть волновой функции:
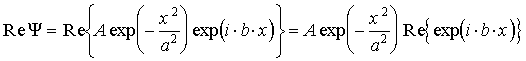 .
По формуле Эйлера из теории комплексных чисел получаем
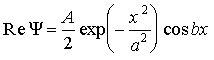 .
б) Определим квадрат модуля волновой функции:
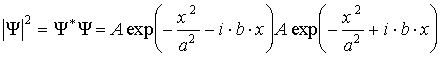 .
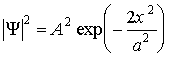 .
Качественный вид найденных зависимостей представлен на рис. 3.3
|