5.6 Дифракция рентгеновских лучей
В природе в роли дифракционных решёток выступают вещества, имеющие кристаллическую структуру. Для таких веществ характерно упорядоченное расположение атомов или молекул в пространстве. При их облучении электромагнитными волнами последние испытывают явление дифракции на атомах или молекулах, в результате становится возможными наблюдать перераспределение интенсивности падающей волны. Структура наблюдаемой дифракционной картины определяется закономерностями расположения атомов и молекул. По этой причине явление дифракции электромагнитных волн может быть использовано для исследования структуры строения вещества, а при известной структуре кристалла - для изучения спектрального состава излучения естественных и искусственных источников излучения.
Выше при изучении свойств дифракционной решёток было установлено, что для увеличения их разрешающей способности и дисперсии расстояние между щелями 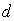 должно быть во много раз больше длины волны 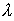 облучающей волны, т. е.
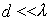 . . | (5.50) |
В кристаллах в роли щелей выступают атомы или молекулы, а период решётки определяется межатомным расстоянием 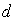 (рис. 5.40). Учитывая, что порядок величины 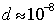 м, для выполнения условия (5.50) необходимо использовать электромагнитные волны с очень малой длиной волны. Для этой цели подходят электромагнитные волны рентгеновского диапазона с длиной волны 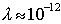 м.
Изучение структуры кристаллических, а также поликристаллических веществ с помощью явления дифракции электромагнитных волн рентгеновского диапазона составляет сущность рентгеноструктурного анализа.
Как известно, структура расположения атомов в кристалле может иметь достаточно сложный, трёхмерный порядок, определяемый т.н. группами симметрии кристалла. Для упрощения рассуждений рассмотрим самый простой случай регулярного расположения атомов в кристаллических плоскостях вдоль прямых линий, параллельных оси 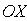 , с межатомным расстоянием 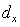 (рис. 5.40). Тогда распределение интенсивности наблюдаемой дифракционной картины будет одинаковым в любой плоскости, проходящей через линии расположения атомов и перпендикулярной кристаллическим плоскостям. 
По этой причине можно ограничиться анализом дифракции плоской рентгеновской волны с длиной 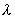 , падающей под углом 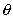 к линии расположения атомов (рис. 5.40). При когерентном рассеянии волн атомами вещества в двух соседних кристаллических плоскостях в направлениях под углами 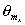 к оси 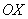 будут формироваться максимумы интенсивности дифракционной картины, если разность хода 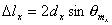 рассеянных волн в этих направлениях кратна длине волны:
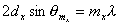 , , | (5.51a) |
где 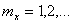 - целые числа.
Выражение (5.51) известно как формула Вульфа - Брэггов. Из этой формулы следует, что при известной длине волны 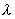 и порядке наблюдаемого дифракционного максимума 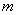 расстояние между кристаллическими плоскостями 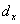 может быть найдено из формулы:
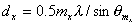 | (5.51b) |
В более общем случае структуры кристалла при наличии порядка расположения атомов вдоль оси 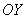 , определяемого межплоскостным расстоянием 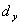 , а также вдоль оси 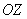 , за которое отвечает межплоскостное расстояние 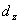 , в результате дифракции рентгеновских волн будут наблюдаться дифракционные максимумы, угловое расположения которых имеет трёхмерный характер и задаётся для каждого из них углами 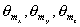 , где 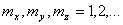 -- целые числа. Положение максимумов и межплоскостные расстояния связаны между собой, соотношениями, следующими из формулы Вульфа - Брэггов (5.51) с учётом угла падения рентгеновской волны на кристалл.
Пусть по отношению к осям выбранной декартовой системы координат XYZ (рис.5.41) направление падения волны составляет углы, равные 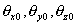 . Между этими углами существует связь, следующая из очевидного соотношения:
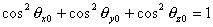 . . | (5.52a) |
С учётом изложенных выше соображений условия формирования дифракционных максимумов в направлениях 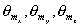 могут быть записаны следующим образом:
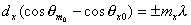 ; ; | (5.53a) |
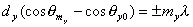 ; ; | (5.53b) |
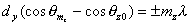 . . | (5.53c) |
Система уравнений (5.53), дополненная условием аналогичным (5.52a)
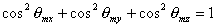 | (5.52b) |
используется для определения искомых значений межплоскостных расстояний 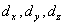
Распределение интенсивности рентгеновских волн при их дифракции на кристалле фиксируется на фотоплёнку, на которой после проявления можно наблюдать светлые и тёмные полосы, кольца, соответствующие дифракционным максимумам и минимумам.
Рассмотрим метод рентгеноструктурного анализа, предложенный Лауэ. В этом методе рентгеновское излучение от источника 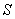 направляется на исследуемый монокристалл и испытывает дифракцию (рис. 5.42). На помещённой за монокристаллом с кристаллической осью 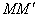 фотопластинке после 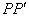 проявления получается совокупность черных точек, соответствующих дифракционным максимумам. Расшифровка записанной таким образом дифракционной картины, называемой лауэграммой, позволяет получить представление о структуре кристалла. На рис.5.43 приведена лауэграмма берилла.
Другой метод рентгеноструктурного анализа был предложен Шерером и Дебаем для исследования поликристаллических образцов. Поликристаллические образцы получаются в результате спекания измельчённого в порошок кристаллического вещества. Изготовленный таким способом образец в форме проволочки  помещается на оси камеры (рис. 5.44), на боковые стенки которой помещается фотоплёнка 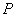 .
При облучении монохроматическим рентгеновским излучением от источника 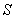 поликристаллического образца 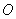 из-за беспорядочной ориентации кристаллических плоскостей различных его составляющих возникает конусы направлений 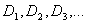 , в которых для рассеянных волн выполнено условие Вульфа - Брэггов.
На плёнке после проявления дифракционная картина ( дебаеграмма) будет иметь вид колец или полос в соответствии с рис. 5.45. Анализ дебаеграммы позволяет определить основные элементы структуры кристалла.
|