5.5 Дифракционная решётка
Периодическая система одинаковых, расположенных на одном и том же расстоянии друг от друга щелей, называется дифракционной решёткой. Расстояние 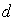 (рис.5.35) между серединами соседних щелей называется периодом дифракционной решётки. Обычно в дифракционных решётках, используемых в оптике, щели являются узкими, т.е. их размер 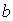 во много раз меньше периода дифракционной решётки 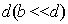 . Размер дифракционной решётки, состоящей из 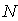 узких щелей, называется её шириной 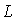 и вычисляется по формуле 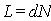 (рис. 5.35).
При освещении дифракционной решётки плоской световой волной с длинной волны 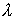 , нормально падающей на решётку, на достаточно большом расстоянии от решётки наблюдается дифракционная картина, которая может наблюдаться и на конечном расстоянии с помощью выпуклой линзы на плоском экране, помещённом в её фокусе (рис. 5.36).
Пусть радиус пространственной когерентности падающей электромагнитной волны 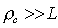 . В этом случае в точке наблюдения 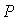 волны от каждой из щелей будут когерентными и комплексная амплитуда, испытавшей дифракцию волны, будет равна сумме комплексных амплитуд волн от каждой из щелей. Для расчёта дифракционной картины создаваемой световым потоком, освещающим решётку, применим подход, использованный в главе 4 для расчёта многолучевой интерференции.
Комплексные амплитуды волн от каждой из щелей решётки, рассчитываемые по формуле (5.25a), учитывающей угловой направленности одинаковых щелей, различаются друг от друга только фазовым множителем. Причём, фазы волн от соседних щелей отличаются на одинаковую величину 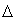 (рис. 5.36):
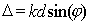 , , | (5.34) |
где 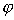 - угол в направлении точки наблюдения 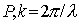 - волновое число.
В соответствии со сказанным комплексная амплитуда 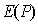 в точке наблюдения будет равна
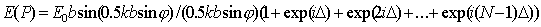 ,
если отсчитывать фазы волн от каждой из щелей по отношению к фазе первой.
Замечая, что сумма в скобках этого выражения представляет собой геометрическую прогрессию со знаменателем 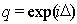 , получим:
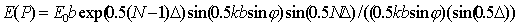 . . | (5.35a) |
Отсюда следует выражение для интенсивности волны I (P) на большом расстоянии от дифракционной решётки
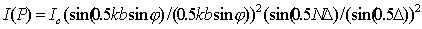 | (5.35b) |
где 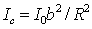 - интенсивность в центре дифракционной картины, расположенном на расстоянии 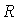 напротив середины дифракционной решётки; 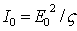 - интенсивность освещающей поверхность дифракционной решётки волны.
Характер распределения интенсивности в соответствии с (5.35b) представляет собой чередование главных дифракционных максимумов, между которыми располагаются побочные дифракционные максимумы и минимумы (рис. 5.42).
Главные дифракционные максимумы интенсивности располагаются в направлениях 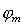 , в которых волны от щелей в точке наблюдения имеют разность хода, кратную 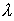 , т.е.:
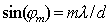 , , | (5.36) |
где 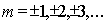 - целые числа.
Главный дифракционный максимум, соответствующий направлению, называется дифракционным максимумом 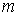 - го порядка. Центральный дифракционный максимум соответственно является дифракционным максимумом нулевого порядка ( 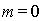 ) и имеет наибольшую величину
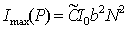 | (5.37) |
По мере увеличения порядка дифракционного максимума его интенсивность уменьшается из-за влияния диаграммы направленности щели. Для узких щелей 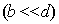 b << d этим уменьшением можно пренебречь.
Если дифракционная решётка освещается белым светом, то все дифракционные максимумы ( 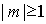 |) за исключением центрального оказываются окрашенными в цвета спектральных составляющих падающей волны. Это является следствием зависимости направления дифракционных максимумов (5.36) от длины волны 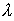 . Спектральные составляющие с меньшей длиной волны располагаются ближе к центру дифракционной картины, а с большей длиной ближе к её периферии.
Свойство дифракционной решётки разделять в пространстве различные спектральные составляющие падающего на неё излучения позволяет её использовать в качестве спектрального прибора, с помощью которого можно исследовать спектры различных источников излучения.
Основными характеристиками дифракционной решётки как спектрального прибора являются такие её параметры, как дисперсия и разрешающая способность.
Дисперсия дифракционной решётки.
Дисперсия дифракционной решётки определяется угловым или линейным расстоянием между дифракционными максимумами, соответствующих спектральным составляющим, длина волны которых отличается на единицу.
Следовательно, математическим выражением для угловой дисперсии 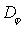 дифракционной решётки является следующее выражение:
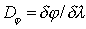 . . | (5.38) |
После дифференцирования по 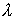 выражения (5.36), определяющего угловые направления максимумов дифракционной решетки, получим:
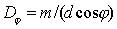 , , | (5.39) |
где 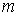 - порядок дифракционного максимума.
Отсюда можно сделать вывод, что наибольшую дисперсию имеет дифракционная решётка при наблюдении максимумов максимально возможного порядка под углами, близкими к скользящим ( 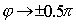 ).
Например, возможно наблюдение окрашенной (радужной) дифракционной картины на такой грубой отражательной дифракционной решётке, которая представляет собой виниловая граммофонная пластинка. Для этого необходимо смотреть вдоль её поверхности на источник света.
Определим максимальное число 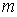 наблюдаемых порядков дифракции в дифракционной решётке наблюдаемых порядков дифракции в дифракционной решётке. Из формулы (5.36) следует, что неравенство 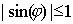 возможно, при условии, что
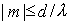 . . | (5.40) |
Линейная дисперсия 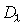 в соответствии с определением может быть найдена из выражения
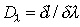 . . | (5.41) |
При наблюдении дифракционной картины в фокальной плоскости линзы (рис. 5.41) очевидно
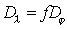 , , | (5.42) |
где 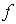 - фокусное расстояние линзы.
Разрешающая способность дифракционной решётки определяется безразмерной величиной
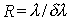 , , | (5.43) |
где 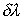 - минимальная разность длин волн спектральных составляющих источника излучения, при которых эти составляющие ещё воспринимаются раздельно.
Критерий раздельного восприятия различных спектральных составляющих источника излучения был предложен Рэлеем. В соответствии с этим критерием, два дифракционных максимума воспринимаются раздельно, если середина одного максимума совпадает с краем (минимумом) другого (рис. 5.38). Такому взаимному расположению разрешаемых максимумов одинаковой интенсивностей соответствует пресечение их распределений на уроне половины от максимального значения (рис.5. 38).
Найдём угловую ширину дифракционного максимума 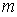 порядка 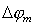 . Очевидно, 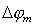 определяется двумя ближайшими минимумами 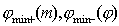 к направлению дифракционного максимума 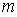 порядка:
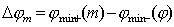 . . | (5.44) |
Направления 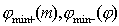 определяются из условия образования замкнутой кривой, суммой комплексных амплитуд от всех щелей:
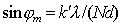 , , | (5.45) |
где 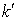 - принимает все целые значения кроме 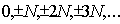
С учётом того, что ближайшие к 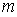 - ому максимуму нули соответствуют значениям 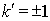 , получаем:
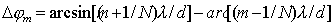 . . | (5.46) |
При большом числе щелей 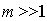 , с помощью дифференцирования находим:
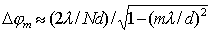 | (5.47a) |
В частности, для центрального максимума 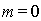 , имеем
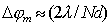 . . | (5.47b) |
Из выражений (5.47a) следует, что угловая ширина дифракционных максимумов обратно пропорциональна ширине решётки ( 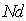 ) и с увеличением 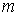 увеличивается. Увеличение связано с тем, что для больших значений 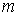 уменьшается эквивалентная ширина дифракционной решётки 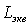 , которая представляет собой проекцию дифракционной решётки на направление, перпендикулярное направлению 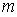 - ого дифракционного максимума (рис. 5.39).
Исходя из (5.36) и (5.45), определим направление 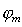 середины максимума 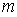 -ого порядка, соответствующего длине волны 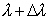
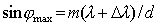 | (5.48a) |
и направления края максимума 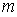 -ого порядка, соответствующего длине волны 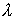
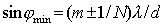 | (5.48b) |
Равенство направлений на середину максимума и края минимума ( 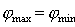 ) двух спектральных составляющих возможно, если выполнено условие равенства выражений (5.48a) и (5.48b):
Отсюда получаем выражение определяющее разрешающую способность дифракционной решётки:
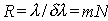 . . | (5.49) |
Из этой формулы следует, что разрешающая способность дифракционной решётки тем, больше, чем больше число щелей 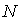 и чем больше порядок дифракционного максимума 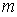 , который используется для разрешения спектральных компонент. Физическая причина такой зависимости разрешающей способности от 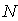 и 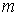 очевидна ввиду того, что при увеличении 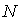 сужаются дифракционные максимумы, а при увеличении 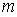 увеличивается угловая дисперсия дифракционной решётки, благодаря чему облегчается раздельное восприятие разрешаемых спектральных компонент.
Дифракционные решётки могут быть использованы для наблюдений, как в проходящем свете, так и в отражённом. Для изготовления дифракционных решёток используют специальную технологию нанесения штрихов на поверхность стекла или металла. Количество штрихов может достигать несколько сотен тысяч. Для металлических решёток штрихи могут наноситься на вогнутую поверхность и в этом случае дифракционные решётки называются вогнутыми. Применение металла для изготовления дифракционных решёток имеет определённые преимущества перед использованием стекла для этих целей. Главное из них возможность более строгого соблюдения периодичности нанесения штрихов на поверхности решётки. Это является следствием меньшей твёрдости металла по сравнению со стеклом, в результате чего меньше изнашивается резец, наносящий штрихи, и периодичность на поверхности металлической дифракционной решётки выдерживается лучше, чем на поверхности стеклянной. Изготовленные высококачественные металлические дифракционные решётки используются для применения более дешёвых копий путём изготовления их отпечатков на желатине. Первая дифракционная решётка была изготовлена в 1785г. американским астрономом Риттенгаузом, но по прямому назначению не использовалась. В 1821г. дифракционная решётка была изготовлена Фраунгофером для спектральных исследований солнечного излучения. Дифракционная решётка Фраунгофера имела порядка нескольких сотен штрихов на сантиметр и изготавливалась путём намотки тонкой проволоки на два параллельных винта. Дальнейшее развитие технологии изготовления дифракционных решёток сделали возможным получение решёток с несколькими десятками тысяч штрихов на сантиметр.
|