5.4 Дифракция Фраунгофера
В соответствии с определением дифракция Фраунгофера наблюдается на большом удалении от препятствия, на которое падает электромагнитная волна (свет). Изучение особенностей этого явления и определение условий его наблюдения рассмотрим на примере дифракции на отверстии в плоском экране плоской электромагнитной волны, падающей на экран перпендикулярно его поверхности (рис. 5.5) в направлении оси 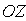 . Без ограничения общности будем полагать, что экран располагается в плоскости 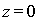 .
Используя приближение Кирхгофа, можно написать следующее из (5.1) выражение для комплексной амплитуды волны в точке наблюдения 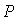 с координатами 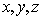 :
 , , | (5.18) |
в котором 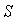 - область, ограниченная контуром отверстия; 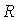 - расстояние от точки интегрирования в области 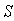 до точки наблюдения 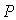 ; 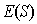 - распределение комплексных амплитуд падающей волны на отверстии; практически постоянная функция направленности вторичных источников 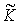 , фигурирующая в выражении (5.1), полагается равной единице.
Упростим выражение (5.18) предполагая, что, во-первых, расстояние z от плоскости экрана с отверстием до точки наблюдения 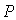 во много раз больше размера отверстия 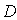 , т.е.:
 . . | (5.19a) |
Это означает, что в точку наблюдения приходит плоская волна. Во- вторых, будем считать, что область определения поля в точке наблюдения P не превышает размеров отверстия 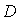 , т.е.:
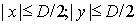 . . | (5.19b) |
Последнее условие обеспечивает применимость приближения Кирхгофа для решения задач дифракции, которое, как было отмечено выше, справедливо для точки наблюдения внутри телесного угла, равного угловому размеру отверстия в экране.
B этом случае можно вынести из под знака интеграла стоящий в знаменателе практически постоянный множитель 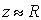 , а в показателе экспоненты этот множитель заменить на
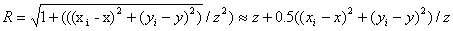 . . | (5.20) |
В результате этих преобразований получим выражение
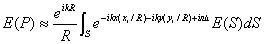 , , | (5.21a) |
 . . | (5.21b) |
которое также может быть упрощено, если в показателе экспоненты подынтегрального выражения (5.21a) пренебречь множителем 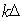 , что имеет место при
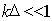 | (5.22) |
Итак, комплексная амплитуда волны в точке наблюдения 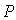 , возникающая из-за дифракции Фраунгофера плоской волны на отверстии в экране, определяется выражением
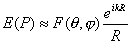 , , | (5.23a) |
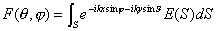 ; ; | (5.23b) |
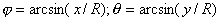 - угловые координаты точки наблюдения P, из 'центра' отверстия.
Из выражения (5.23a) следует, что при дифракции Фраунгофера в точку наблюдения приходит сферическая волна, практически не отличающаяся при условии (5.22) от плоской волны с направления, под которым 'виден' центр отверстия из точки P. Амплитуда этой волны определяется выражением (5.23b), определяющим функцию 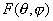 , получившую название диаграммы направленности. Если в точку наблюдения 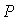 поместить экран, то наблюдаемое на нём распределение интенсивности света 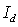 будет определяться квадратом модуля этой функции, т.е.
 , , | (5.24) |
где 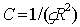 - константа пропорциональности, определяемая пройденным волной расстоянием от отверстия до точки наблюдения и волновым сопротивлением среды.
Распределение интенсивности на экране при наблюдении дифракции Фраунгофера на экране с отверстием будет иметь вид чередующихся тёмных и светлых полос или колец в зависимости от числа открытых зон Френеля.
Рассмотрим более подробно дифракцию Фраунгофера плоской электромагнитной волны на щели шириной 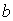 в плоском экране, ориентированном перпендикулярно направлению распространения волны (рис. 5.26a). В соответствии с симметрией задачи искомое поле 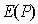 будет одинаковым в любой плоскости, перпендикулярной экрану, т.е. 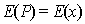 не будет зависеть от 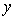 , а диаграмма направленности 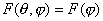 не будет зависеть от угла координаты 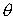 . Из выражения (5.23b) находим диаграмму направленности 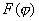 волны, испытавшей дифракцию на экране:
 , , | (5.25a) |
где 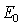 - амплитуда падающей на щель плоской волны, фаза которой в плоскости щели полагается равной нулю.
Распределение интенсивности 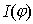 дифракционной волны, рассчитываемое в соответствии с (5.24) и (5.25a), может быть определено с помощью следующего выражения:
 , , | (5.25b) |
где 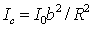 - интенсивность в центре дифракционной картины, расположенном напротив середины щели; 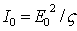 - интенсивность освещающей поверхность щели волны.
На рис. 5.29 приведен график распределения интенсивности дифракционной волны как функции от безразмерной переменной 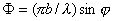 , масштаб которой определяется размером щели 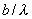 , выраженным в длинах волн. Распределение имеет главный максимум в направлении распространения падающей на щель волны и быстро убывающие по мере удаления в тень побочные максимумы.
Главному максимуму соответствует освещённая область, а побочным - убывающие по интенсивности светлые полосы равной ширины, параллельные краям щели. Величина главного максимума 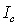 распределения интенсивности дифракционной волны пропорциональна квадрату ширины щели 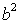 .Угловой размер наблюдаемого главного дифракционного максимума 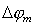 оценим расстоянием между первыми нулями функции 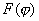 при смещении из центра картины в зону тени Это не единственный способ определить угловую ширину наблюдаемого дифракционного пятна. Согласно Рэлею ширина пятна определяется разностью угловых координат, соответствующих уменьшению максимального значения интенсивности в два раза. Оказывается, что в большинстве практических случаев " рэлеевская " ширина полосы (пятна) меньше ширины 'по нулям' в примерно в два раза .
Для щелей, освещаемых световыми волнами, практически всегда выполняется условие ( 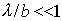 ). В соответствии с этим условием получаем , что угловой размер наблюдаемой дифракционной полосы
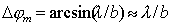 | (5.26a) |
обратно пропорционален ширине щели, выраженной в длинах волн.
Можно показать, что 96% мощности светового потока при его дифракции на щели сосредоточено в пределах телесного угла 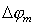 .
Если для наблюдения дифракции Фраунгофера используется линза с фокусным расстоянием 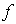 (рис. 5.30), позволяющая видеть дифракционную картину в её фокальной плоскости на конечном расстоянии от препятствия, то найденному значению угловой ширины дифракционного пятна соответствует его ' линейная ' ширина 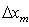 :
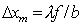 . . | (5.26b) |
Отсюда следует, что использование для наблюдения дифракции длиннофокусных линз с большим 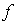 позволяет получить на экране визуально различимые светлые и тёмные дифракционные полосы.
Характер дифракционной картины света на щели, установленный расчётным путём с помощью (5.23b), полностью совпадает с выводами, которые следуют из применения для решения рассматриваемой задачи графико - аналитического метода зон Френеля.
В самом деле, при формировании главного максимума дифракционной картины при 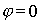 волны от всех элементов щели складываются в фазе (рис.5.31a) и значение поля в этом направлении пропорционально сумме длин упомянутых выше бесконечно малых элементов щели , т.е. ширине щели 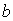 . Из (5.23) при 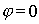 также получается значение пропорциональное 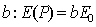 . Для дальнейшего в целях упрощения примем амплитуду волны, освещающую щель, равной единице. Тогда амплитуда дифракционной волны в направлении главного максимума будет равна 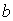 .
Рассмотрим формирование минимумов при дифракции на щели. С точки зрения метода зон Френеля (рис.5.31b) волны, создаваемые множеством бесконечно малых элементов, на которые можно разбить щель, приходят в точку наблюдения так, что их суммарная амплитуда равна нулю. В этом случае, зонная диаграмма Френеля представляет собой замкнутую кривую (окружность) начало и конец которой совпадают друг с другом. Например, зонная диаграмма Френеля, соответствующая первым дифракционным минимумам ( 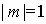 ), является 'зонной' окружностью длиной 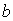 . Зонные окружности, соответствующие противоположным знакам 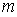 , имеют противоположные направления обхода.
Зонная диаграмма Френеля, соответствующая вторым, дифракционным минимумам ( 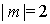 ), представляет собой две вложенные 'зонные' окружности, общая длина которых равна 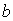 . Зонная диаграмма Френеля, соответствующая дифракционным минимумам с номером 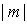 , представляет собой в этом случае 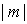 вложенных 'зонных' окружностей, общая длина которых равна 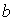 . В буквальном смысле дифракционному минимуму с номером 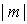 соответствует 'накручивание' отрезка длиной 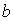 вокруг фокуса спирали Корню на 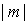 оборотов .
Каждому из оборотов зонной окружности соответствует приращение фазы вектора комплексной амплитуды дифракционной волны, равное 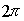 . Следовательно, угловое направление 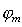 на дифракционный минимум с номером 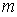 определится из условия
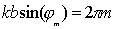 | (5.27) |
где 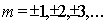 ...- целые числа, определяющие номер или порядок дифракционного максимума.
Это выражение в точности следует из (5.25b) и определяет угловые направления 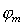 , в которых формируются минимумы интенсивности дифракционного поля
Сравним, наконец, значения побочных дифракционных максимумов, находимые с помощью метода зон Френеля и из (5.25b) при
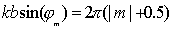 , , | (5.26a) |
где 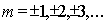 - порядок дифракционного максимума, определяется одинаковой быстро убывающей последовательностью чисел
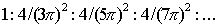 . . | (5.26b) |
В самом деле, побочным дифракционным максимумам соответствует такое сложение волн (рис.5.31c) от малых элементов щели, при котором результирующий вектор приближённо совпадает с диаметром 'зонной ' окружности. Заметим, что 'зонная' окружность соответствующая побочному дифракционному максимуму с номером 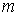 получается, как было отмечено выше, в результате 'накручивания' отрезка длиной 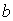 вокруг фокуса спирали Корню на 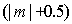 оборотов. Диаметр окружности 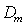 , соответствующей таким оборотам, определяется из формулы:
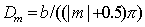 . . | (5.28c) |
Следовательно, учитывая, что значения соответствующих максимумов интенсивности света пропорциональны 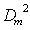 , получаем ту же последовательность чисел, что и (5.28b).
Дифракция Фраунгофера на круглом отверстии.
Рассмотрим задачу фраунгоферовой дифракции на круглом отверстии диаметром 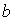 в непрозрачном экране плоской электромагнитной волны с длиной волны 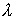 , падающей перпендикулярно плоскости экрана (рис. 5.14). Как следует из расчётов по формуле (5.23b) в этом случае для малых углов дифракции 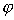 распределение интенсивности дифракционной волны описывается бесселевой функцией первого порядка 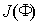 от безразмерной переменной 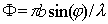 :
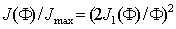 ,
где 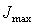 - максимальное значение интенсивности света в центре дифракционной картины.
Распределение интенсивности, наблюдаемое на экране, представляет собой семейство концентрических убывающих по величине максимумов, разделённых минимумами (тёмных и светлых колец при наблюдении дифракции света), вокруг главного дифракционного максимума (рис. 5.32). Ширина главного дифракционного максимума 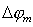 определяется диаметром отверстия
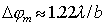 . . | (5.29) |
Числовой коэффициент в (5.29) зависит от распределения интенсивности волны, падающей на отверстие, и от формы отверстия. Если распределение интенсивности уменьшается к краю отверстия, то этот коэффициент увеличивается по величине. Обратим внимание, что при 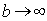 ширина дифракционного максимума стремится 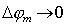 . Это означает, что только при освещении линзы бесконечно большого размера плоской волной возможна её точная фокусировка в точку. Для линз конечного размера выражение (5.29) определяет возможный дифракционный предел качества изображения, которое может быть получено в оптической системе, состоящей из линз, зеркал, объективов, размеры которых заданы конструкцией этих приборов. В связи с этим, когда говорят о дифракционной разрешающей способности объектива диаметром 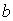 , то имеется ввиду оценка минимально возможного углового расстояния между точечными объектами по формуле (5.29), при котором они могут быть различены при наблюдении их изображения в фокальной плоскости этого объектива. Это определение разрешающей способности объектива основано на предложенном Рэлеем критерии разрешения, более подробно с которым мы познакомимся в следующем параграфе.
Рассмотренное выше формирование максимумов и минимумов при дифракции Фраунгофера на щели имеет общий характер при дифракции на препятствиях другого вида. С помощью (5.23) можно показать, что при дифракции Фраунгофера электромагнитной волны на произвольном препятствии, размер которого равен 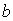 , угловой размер области главного максимума дифракционного поля от препятствия, может быть оценён с помощью формул (5.30).
На рис. 5.33 приведена фотография распределения интенсивности света при наблюдении дифракции Фраунгофера на круглом отверстии в непрозрачном экране, изображение которого вполне согласуется с приведенными выше рассуждениями.
Для наблюдения дифракции Фраунгофера должно быть выполнено условие (5.22). Определим соотношение между размером отверстия 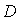 и расстоянием 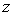 , при котором приходящую в точку наблюдения волну ещё можно считать плоской (рис. 5.34).
Заметим, что введённый выше в (5.21b) параметр 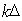 определяет отличие фаз сферической и плоской волн, приходящих в точку наблюдения от отверстия. Поэтому в качестве предельно допустимого значения этого параметра можно выбрать его значение, равное 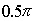 , т. е. 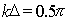 . Используя неравенства (5.19b), с учётом конечного размера отверстия ( 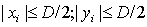 ), получим искомую взаимосвязь между 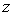 и 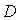 :
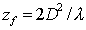 | (5.30) |
Таким образом, для наблюдения дифракции Фраунгофера на отверстии размером 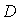 точка наблюдения должна находиться на расстоянии 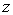 , превышающем 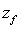 , т.е.:
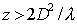 | (5.31a) |
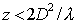 , , | (5.31b) |
то приходящие в точку наблюдения волны будут существенно отличаться от плоских и в точке наблюдения будет иметь место наиболее общий случай дифракции, называемый дифракцией Френеля.
В пределе при очень малых расстояниях точки наблюдения от отверстия
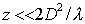 | (5.32c) |
можно пренебречь фазовыми набегами волн от отверстия и считать, что свет распространяется вдоль лучей по законам геометрической оптики.
Если учесть, что в соответствии с выражение (5.12) площадь первой зоны Френеля, открываемой из точки наблюдения на расстоянии 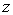 от экрана, равна 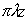 , а 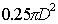 площадь отверстия, то условия (5.24) можно переписать в виде оценки числа открытых зон Френеля 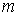 :
а) для наблюдения дифракции Фраунгофера должна быть открыта меньшая часть первой зоны Френеля, т. е.
 ; ; | (5.33a) |
б) для наблюдения дифракции Френеля должно быть открыто несколько зон Френеля, т.е.
 ; ; | (5.33b) |
в) для применимости геометрической оптики должно быть открыто большое число зон Френеля, т. е.
 . . | (5.33c) |
Числа в этих неравенствах, указывающие границы возможности наблюдать тот или иной вид дифракции ( или вообще не наблюдать дифракцию, как это имеет место для геометрической оптики ) имеют условное значение, которое на практике определяется точностью, предъявляемой к решению рассматриваемой задачи дифракции.
|