5.2 Зоны Френеля
Как следует из принципа Гюйгенса- Френеля комплексная амплитуда волны в точке наблюдения 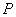 (рис. 5.4), создаваемая источником монохроматической электромагнитной волны в точке 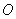 , может быть найдена как суперпозиция комплексных амплитуд сферических волн, испускаемых вторичными источниками на произвольной замкнутой поверхности 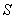 , охватывающей точку 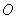 в соответствии с выражением (5.1). Пусть 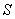 сферическая поверхность радиуса 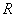 c центром в точке 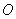 . Тогда поле 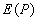 в точке наблюдения 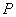 можно представить суммой полей 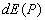 , доставляемых электромагнитной волной от бесконечного множества шаровых сегментов 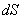 (рис. 5.10):
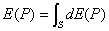 . . | (5.5) |
Рассмотрим 'механизм' формирования значения поля 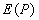 последовательно, начиная от центрального шарового сегмента, центр которого пересекается прямой, соединяющей точки 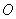 и 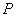 (рис. 5.10). Приближённо на первом этапе рассуждений можно полагать, что амплитуды волн от соседних шаровых сегментов равны. Однако фазы этих волн отличаются из-за того, что волны проходят разный путь, тем больший, чем дальше рассматриваемый сегмент расположен от центрального (рис. 5.10). В первом приближении, можно полагать, что фаза меняется линейно в зависимости от пройденного волной расстояния от соответствующего шарового сегмента. По этой причине комплексная амплитуда 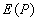 , определяемая (5.5), представляет собой сумму бесконечно большого количества комплексных векторов одинаковой амплитуды, но повёрнутых по отношению к соседнему на одинаковый, бесконечно малый угол. На рис. 5.11a показано в виде комплексного вектора значение 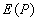 , соответствующее такой части поверхности 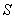 , когда малые шаровые сегменты создают в точке наблюдения поле, фаза которого отличается на 180 о от фазы волны центрального сегмента. Рассмотренная часть поверхности 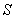 волнового фронта получила название первой зоны Френеля. Границей, отделяющей первую зону Френеля от остальной части поверхности волнового фронта 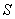 , является окружность, в каждой точке которой фаза волн, приходящих в точку наблюдения 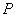 , отличается на 180 о от фазы волны центрального сегмента.
Обратим внимание, что комплексная амплитуда поля, создаваемая первой зоной Френеля, определяется вектором, обозначаемым 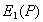 и совпадающим с диаметром полуокружности, к которой стремится в пределе годограф кривой, представляющей сумму полей, создаваемых бесконечно малыми шаровыми сегментами. Фаза волны, создаваемой первой зоной Френеля, как следует из рис. 5.11a , отстаёт на 90 о от фазы волны 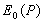 , создаваемой центральным сегментом.
Если подвергнуть поверхность 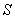 дальнейшему разбиению на зоны, то получим вторую зону Френеля (рис. 5.12), граничащую с первой зоной и отделённую от остальной части поверхности 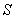 окружностью, в каждой точке которой фаза волн, приходящих в точку наблюдения 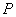 отличается на 180 о от фазы волн от границы с первой зоной Френеля. Можно заметить, что волны от второй зоны Френеля уменьшают комплексную амплитуду волн, создаваемых первой зоной Френеля, ввиду их противофазного сложения. В первом приближении, если не учитывать убывание амплитуды сферических волн обратно пропорционально расстоянию, сумма волн от первой и второй зон Френеля равна нулю. Но на самом деле, сумма волн, создаваемых первой и второй зоной Френеля хотя и имеет малую величину, но не равна нулю. Поэтому характер годографа волн, создаваемых первой и второй зоной Френеля, в пределе представляет часть некоторой спирали (рис. 5.11b).
Аналогичным образом продолжая разбиение поверхности 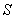 на зоны, т.е. рассматривая третью, четвёртую и т.д. зоны Френеля (рис. 5.12), получим, что соседние чётные и нечётные зоны Френеля ослабляют поля, создаваемые каждой, и вместе образуют годограф, определяющий в пределе величину поля источника 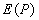 в точке наблюдения, в виде некоторой спирали (рис. 5. 11c).
Границам зон Френеля на спирали соответствуют диаметрально противоположные точки её витков (рис. 5.11c), каждой из которых, соответствуют определяющие её границы радиус на поверхности 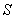 . Так, граница 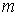 - ой зоны Френеля ( 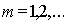 ) отстоит от прямой 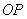 (рис. 5.12) на расстоянии 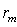 , называемом радиусом 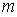 - ой зоны Френеля. Найдём радиус 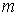 - ой зоны Френеля. Как следует из геометрических соображений (рис. 5.13a):
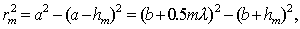 | (5.6a) |
где 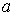 - расстояние вдоль прямой 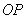 от источника до центра волнового фронта ; 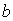 - расстояние вдоль прямой 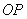 от центра волнового фронта до точки наблюдения.
Из (5.6a), пренебрегая 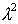 , для не очень больших 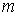 найдём 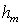 :
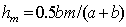 . . | (5.6b) |
С помощью этого соотношения из (5.6а) найдём
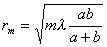 | (5.6c) |
В частном случае бесконечно удалённого источника от точки наблюдения ( 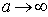 ) волновой фронт 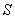 является плоскостью и
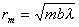 . . | (5.6d) |
Характерной особенностью спирали (рис. 5.11c) является положение фокуса этой кривой, на который она 'наматывается' при бесконечно большом числе зон Френеля. Покажем, что фокус располагается в центре полуокружности первого витка спирали (рис. 5.11c), т.е. величина, поля создаваемого первой зоной Френеля, в два раза больше величины поля, создаваемой источником 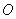 в точке наблюдения 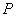 .
Действительно, пусть 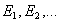 - комплексные амплитуды, создаваемые первой, второй и т.д. зонами Френеля. Тогда искомая комплексная амплитуда в точке 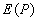 , создаваемая всеми зонами Френеля в точке наблюдения, равна
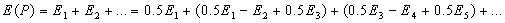 . . | (5.7) |
Как было отмечено выше, можно считать, что вклады от соседних зон примерно равны и их величины монотонно уменьшаются. По этой причине можно считать выражения в скобках в (5.7) равными нулю, т. е. имеет место равенство для любого 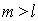 :
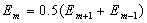 .
Тогда из выражения (5.7) получим:
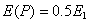 . . | (5.8) |
Учитывая, что интенсивность волны пропорциональна квадрату модуля электромагнитных векторов, можно заключить, что интенсивность поля 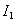 , создаваемого первой зоной Френеля, в четыре раза больше интенсивности волны источника 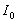 в точке наблюдения, создаваемой всеми вторичными источниками на поверхности 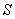 :
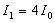 | (5.9) |
Четырёхкратное уменьшение интенсивности волны, создаваемой первой зоной Френеля, по отношению к интенсивности волны, создаваемой источником в точке наблюдения, связано с упомянутым выше противофазным вычитанием волн от различных зон Френеля на поверхности волнового фронта.
Приближённо, не принимая во внимание уменьшение интенсивности сферической волны с расстоянием, которое она проходит, в расчётах можно полагать, что величиной (5.9) определяется интенсивность волны, создаваемой каждой из зон Френеля, близкой к первой. Это является следствием равенства площадей зон Френеля, соответствующих различным значениям m. Действительно, принимая во внимание (рис. 5.13), находим площадь 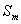 сферического сегмента радиуса 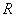 и высоты 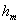
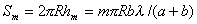 , , | (5.10a) |
и получаем, что площадь 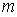 - ой зоны Френеля 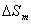 :
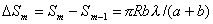 , , | (5.10b) |
не зависит от 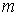 .
Разбиение волнового фронта электромагнитной волны на зоны Френеля широко используется для решения различных оптических задач.
|