5.1 Принцип Гюйгенса-Френеля
Понятие о дифракции электромагнитных волн и её видах.
В гл.3 была рассмотрена задача распространения электромагнитной волны в однородной, неограниченной среде, диэлектрическая 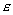 и магнитные  проницаемости которой постоянны в любой точке среды и не зависят от времени . Исследуем взаимодействие электромагнитной волны с неоднородностями среды, в качестве которых можно мыслить любые материальные объекты на пути распространения волны, границы, разделяющие различные среды, области пространства, где значение электрофизических параметров могут зависеть от координат точки наблюдения и/или от времени.
Физическое явление взаимодействия электромагнитной волны с неоднородностями пространства называется дифракцией электромагнитной волны, в частности, дифракцией света. Благодаря дифракции света возникают волны (рис. 5.1), отражённые от освещаемых объектов, и становится возможным их визуализация (" видение "). Дифракция световых волн определяет качество оптических приборов, в частности их разрешающую способность.
Выше в гл.3 при определении коэффициентов прохождения и отражения плоской электромагнитной волны от плоской границы раздела двух сред с различными значениями 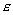 и 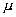 по существу была решена простейшая дифракционная задача.
Различают два вида явления дифракции в зависимости от расстояния точки наблюдения до препятствия или неоднородности, а также от вида волнового фронта в точке наблюдения. Если точка наблюдения расположена достаточно далеко от препятствия и в точку наблюдения после взаимодействия с неоднородностью приходит плоская волна, то говорят о дифракции Фраунгофера. В остальных случаях говорят о дифракции Френеля. Критерии наблюдения дифракции Френеля или Фраунгофера в зависимости от соотношения между длиной волны, размером препятствия и расстояния до точки наблюдения мы рассмотрим ниже в под разделе 5.4.
В качестве примера рассмотрим взаимодействие светового потока от источника  с непрозрачной плоской преградой, в которой прорезано отверстие произвольной формы. При дифракции Френеля (рис. 5.2a) в точку наблюдения 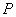 , расположенную на экране на конечном расстоянии 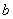 от преграды, приходят сферические волны от источника, расположенного на конечном расстоянии 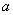 от преграды, и от точек контура, ограничивающего отверстие. При дифракции Фраунгофера (рис. 5.2b) световой волны от источника 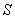 , бесконечно удалённого от преграды, в точку наблюдения 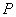 , также бесконечно удалённую от преграды, приходят плоские волны.
Отсюда следует, что дифракция Френеля проявляется в виде интерференции сферических (цилиндрических) волн, приходящих в точку наблюдения от неоднородности, с которой взаимодействует электромагнитная волна (свет). Интерференция цилиндрических волн, представляющая собой частный случай интерференции сферических волн, имеет место в том случае, когда и световая волна и неоднородность среды распространения обладают общей осью симметрии, вследствие которой поле волны и параметры неоднородности одинаковы в любом сечении, перпендикулярном оси симметрии.
Дифракция Фраунгофера обусловлена интерференцией параллельных, плоских волн (лучей), приходящих в точку наблюдения от неоднородности, с которой взаимодействует электромагнитная волна (свет). С помощью линзы 2 (рис. 5.3)
дифракцию Фраунгофера можно наблюдать на экране, расположенном на конечном расстоянии от преграды, с которой взаимодействует свет (электромагнитная волна). Линза 1 (рис. 5.3), в фокусе которой расположен источник 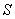 , используется для освещения отверстия в преграде плоской волной.
Формулировка принципа Гюйгенса - Френеля.
Важный шаг в понимании явления дифракции электромагнитных волн был сделан Гюйгенсом, который объяснил процесс распространения волны от некоторого источника 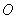 с помощью суперпозиции (интерференции!) излучения "вторичных "источников 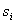 , которые могут быть размещены на фронте 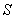 распространяющейся волны в произвольный момент времени 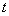 (рис. 5.4). В соответствии с принципом Гюйгенса положение волнового фронта 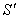 волны в момент времени 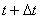 t определяется огибающей фронтов сферических волн,
излучаемых в момент времени 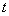 упомянутыми выше вторичными сферическими источниками. Одной из особенностей излучения вторичных источников является их направленность по отношению к направлению распространения волны. Направленность излучения этих источников проявляется в отсутствии излучения в направлении назад к источнику. Большая роль в развитии и применении принципа Гюйгенса принадлежит Френелю, который принял во внимание интерференцию волн вторичных источников, выражающуюся в том, что поле в произвольный момент времени в точке наблюдения волны является суммой сферических волн, излучённых вторичным источниками в предыдущий момент времени с учётом их интерференции.
В целях упрощения дальнейших рассуждений рассмотрим математическую формулировку принципа Гюйгенса - Френеля применительно к гармоническим электромагнитным волнам с произвольно поляризованными колебаниями вектора напряжённости электрического поля волны 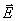 .
Как было отмечено в главе 4, для гармонических электромагнитных волн удобно использовать комплексные амплитуды векторов полей, зависящие только от координат точки наблюдения.
В соответствии с принципом Гюйгенса - Френеля в точке наблюдения 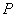 (рис. 5.5.) комплексная амплитуда вектора напряжённости электрического поля 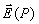 гармонической электромагнитной волны может быть вычислена по формуле:
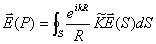 , , | (5.1) |
где 1) 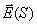 - распределение комплексных амплитуд вектора напряжённости электрического поля источника 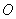 на произвольной замкнутой поверхности 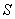 , охватывающей источник 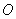 ;
2) 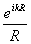 - комплексная амплитуда вторичных источников сферических волн на поверхности 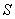 ;
3) 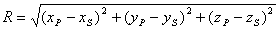 - расстояние от точки расположения вторичного источника с координатами ( 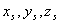 ), расположенного на поверхности 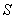 , до точки наблюдения с координатами ( 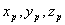 );
4) 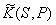 - медленно меняющаяся функция в зависимости от положения точек 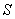 и 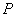 , учитывающая направленность вторичных излучателей, которую приближённо можно считать равной единице за исключением случая расположения точки наблюдения 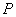 внутри 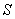 , когда она полагается равной нулю.
Поскольку следующие ниже рассуждения справедливы для любой из декартовых компонент 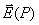 , далее символ вектора будем опускать, понимая, что полученные выражения справедливы для каждой из них.
Большое значение для решения задач дифракции с помощью принципа Гюйгенса-Френеля имели оптические исследования Кирхгофа. Кирхгоф предложил простой способ решения задач дифракции на основе выражения (5.1), дополнив его правилами преобразования волновых фронтов на граничных поверхностях неоднородностей. В качестве характерных неоднородностей далее рассмотрим следующие две:
а) непрозрачный, плоский экран, содержащий отверстие произвольной формы (рис. 5.6a);
б) непрозрачная, плоская пластинка произвольной формы (рис. 5.6b).
Согласно Кирхгофу для решения задачи дифракции электромагнитной волны от точечного источника, облучающего отверстие в непрозрачном экране (задача 'а'), необходимо рассчитать интеграл (5.1), полагая 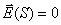 на поверхности экрана, а на поверхности отверстия 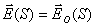 , где 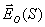 - напряжённость электрического поля на поверхности S в месте нахождения отверстия, которое создается источником в отсутствии экрана.
Для решения задачи б) необходимо рассчитать интеграл (5.1), полагая 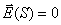 на поверхности пластинки, а вне поверхности отверстия 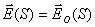 , где 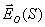 - напряжённость электрического поля на поверхности 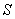 вне пластинки, которое создается источником в отсутствии пластинки.
Такой подход к решению задач дифракции известен как приближение Кирхгофа. Приближение состоит в том, что правило расчёта полей на отверстии и на пластинке не учитывает отражение волн от краёв отверстия (задача 'а') или пластинки (задача 'б'). Однако в большинстве случаев расчёта полей на расстояниях, значительно превышающих размера отверстия (задача 'а') или пластинки (задача 'б'), погрешностью вычислений из-за учёта данного фактора можно пренебречь. Строгие исследование области применимости решения задач дифракции с помощью приближения Кирхгофа ограничивают её телесным углом (рис. 5.7), под которым виден объект дифракции (в нашем случае - отверстия или пластинки).
В этом случае приближённые значения полей отличаются от точных не более чем на 5%, что достаточно для большинства практических приложений, использующих решение задач дифракции.
Приближение Кирхгофа является достаточно гибким и удобным методом решения разнообразных задач дифракции. В качестве примера рассмотрим схему применения приближения Кирхгофа для решения задачи дифракции поля точечного источника на линзе, находящейся в непрозрачном экране. Заметим, что данная задача является ключевой для расчёта оптических систем, поскольку линзы в микроскопах, телескопах, зрительных трубах, объективах видео и фотокамер, различных голографических приборах и др. являются основными устройствами, формирующими изображение.
Прежде всего, дадим функциональное определение, бесконечно тонкой линзы, как оптического прибора, вносящего квадратичные изменения фазы волны в каждой точке своей поверхности (в нашем случае 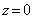 , рис.5.8a) на величину 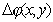 , определяемую следующим выражением:
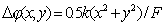 , , | (5.2a) |
где 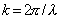 - волновое число; 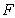 - фокусное расстояние линзы.
Фазовый набег, соответствующий (5.2a) получается при изготовлении линзы из диэлектрика с показателем преломления 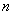 и придания сферической формы его внешней поверхности.
Покажем, что плоская волна 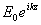 , распространяющаяся вдоль оси OZ, после прохождения такого прибора превращается как в линзе в сферическую волну. Действительно, фаза 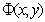 этой волны за плоскостью 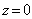 будет такой же, как у сферической волны, поскольку для 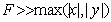 :
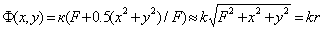 ,
где 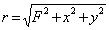 - расстояние, которое проходит сферическая волна, излучаемая из точки 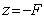 на оси 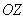 , в точку плоскости 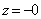 с координатами 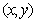 . В силу того, что лучи, соответствующие сферической волне, пересекаются в точке 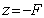 при их продолжении в противоположном направлении относительно распространяющейся волны (5.8b), точка 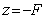 является фокусом рассеивающей линзы. Для рассеивающей линзы в соответствии с (5.2a) характерно квадратичное возрастание фазовой задержки от нуля в центре к периферии.
Наоборот, для собирающей линзы, характерно квадратичное уменьшение фазовой задержки от максимума в центральной части линзы к её периферии (рис. 5.9a,b). Вносимые собирающей линзой квадратичные изменения фазы 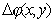 проходящей волны могут быть определены аналогичным (5.2a) выражением:
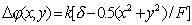 , , | (5.2b) |
где 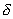 - толщина линзы; 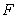 - фокусное расстояние линзы.
Пусть круглая линза радиуса 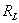 располагается в плоскости 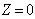 в начале координат (рис. 5.8). Тогда для решения задачи дифракции на линзе надо взять интеграл (5.1) по поверхности круга радиуса 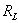 , определяя в подынтегральном выражении 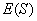 с учётом изменения фазы волны источника 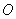 линзой, т.е.
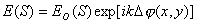 , , | (5.2c) |
где 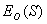 - поле источника 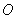 на поверхности линзы, если бы линзы не было; 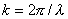 - волновое число; 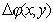 - соответствующий рассеивающей (5.2a) или собирающей (5.2b) линзе вносимый фазовый набег.
Как правило, при расчёте задачи дифракции на линзе можно пренебречь изменением амплитуды падающей волны на поверхности линзы, т.е. полагать её постоянной 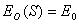 . В этом случае для расчёта дифракционных полей получаются интегралы, известные в оптике как интегралы Френеля.
В современной практике научных, прикладных и инженерных приложений исследований в области электромагнитных волн решение задач дифракции довольно часто получают с помощью методов, являющихся по существу модификациями приближения Кирхгофа. В частности, в таких широко известных современных методах решения задач дифракции, как геометрическая теория дифракции и метод краевых волн, делается попытка учесть волны отраженные от краёв отверстия, кривизну облучаемых тел и токи, возникающие на экране вблизи его краёв.
Связь решений задач дифракции электромагнитных волн на отверстии в непрозрачном экране и на непрозрачном диске, совпадающим по форме с отверстием (Принцип Бабине).
Рассмотрим две модельные задачи дифракции электромагнитной волны от одного итого же источника 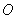 на экране с отверстием и на пластинке, контур которой совпадает с контуром отверстия (рис. 5.6). Такие два объекта дифракции являются взаимно дополняющими друг друга в том, смысле, что если совместить пластинку с отверстием, то получится плоский непрозрачный экран. Ввиду этого решение задач на взаимно дополняющих экране и отверстии связаны друг с другом.
Пусть 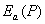 - решение задачи дифракции волн на экране с отверстием от источника, находяшегося в точке 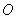 , а 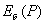 решение задачи дифракции волн на дополнительном экране (пластинке) от того же источника. Тогда согласно принципу Бабине в точке 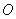 в точке наблюдения 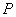 будет иметь место:
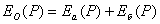 , , | (5.3) |
где 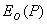 - поле источника в точке наблюдения в отсутствии экрана или пластинки.
Принцип Бабине позволяет найти решение задачи дифракции на экране с отверстием, если известно решение задачи пластинке являющейся дополнительной к отверстию в экране и наоборот.
Из принципа Бабине в частности следует, что если в точке наблюдения интенсивность 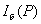 равна нулю, то 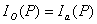 . Если же 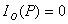 , то  . И наконец, если плоские дополнительные экраны облучает плоская волна с интенсивностью 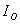 , падающая перпендикулярно плоскости экрана, то в соответствии с главой 6 и (5.3) взаимосвязь интенсивностей 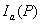 и 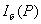 дифракционных полей на двух дополнительных экранах определяется разностью фаз 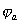 и 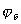 этих полей в точке наблюдения:
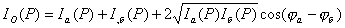 | (5.4) |
С помощью современных электронно-вычислительных машин можно получить решение любой задачи дифракции электромагнитных волн на произвольном теле с помощью выражения (5.1) или более строгих соотношений, учитывающих векторную структуру электромагнитных волн. Однако в ряде случаев удаётся получить не только качественные представления о дифракции электромагнитных волн на том или ином объекте, но и достаточно точно оценить интенсивность соответствующего дифракционного поля, понять принцип работы многих оптических устройств, оптимизировать их характеристики, не прибегая к сложным арифметическим расчётам. Для этой цели используется предложенное Френелем понятие зон Френеля, рассматриваемое в следующем параграфе.
|