4.6 Эффект Вавилова-Черенкова
Рассмотрим движение заряженной частицы, например, электрона в некоторой среде вдоль прямой линии с постоянной скоростью 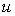 , превышающей фазовую скорость света 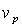 в этой среде. Своим полем частица возбуждает колебания электронных оболочек атомов или молекул среды и они становятся центрами излучения электромагнитных волн. При равномерном движении частицы это излучение может считаться когерентным. Тогда электромагнитные волны, излучаемые атомами и молекулами среды, могут интерферировать между собой, формируя в определённых направлениях интерференционные максимумы. В соответствии со сказанным выше условием формирования интерференционного максимума является сложение в некоторой точке наблюдения 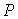 (рис. 4.30), расположенной в бесконечно удалённой точке от линии движения заряженной частицы, в фазе волн, излученных в различные моменты времени 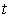 . Пусть 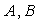 две выделенные точки на линии движения заряженной частицы, которые она проходит в моменты времени 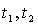 (рис. 4.30) . Отрезок 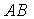 на своей траектории заряженная частица проходит за промежуток времени 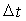 равный
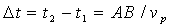 .
В точку наблюдения 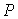 электромагнитные волны, излучённые из точек 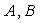 , придут в моменты времени соответственно равные: 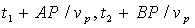 .
Найдём разность времён 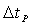 прихода в точку наблюдения 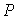 волн, излученных из точек 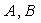 линии движения заряженной частицы:
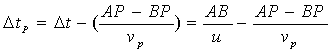 .
Если 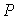 находится на достаточно большом удалении от линии движения заряженной частицы, то можно полагать, что
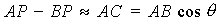 .
 .
Учитывая, что 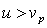 , одновременный ( 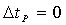 ) приход электромагнитных волн в точку наблюдения 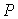 возможен в направлении, определяемым углом 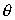 из условия:
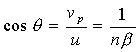 , , | (4.29a) |
где 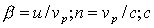 - скорость света в вакууме; 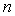 - показатель преломления среды.
Таким образом, при движении заряженной частицы со скоростью большей скорости света в этой среде ( 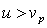 ) , возникает излучение электромагнитных волн, максимум которого располагается на конической поверхности с осью вдоль направления движения частицы и углом 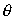 образующей с осью, равным
 . . | (4.29b) |
В других направлениях, отличных от указанного излучаемые атомами и молекулами электромагнитных волны не будут складываться в фазе , т.е. будут гасить друг друга .
Излучение электромагнитных волн движущимся зарядом впервые было обнаружено в 1934г., а затем экспериментально исследовано Вавиловым С.И. (1891-1951) и Черенковым П.А.(р.1904). В честь своих первооткрывателей излучение получило название - Вавилова и Черенкова. Черенков П.А. показал, что все жидкие и твёрдые тела при прохождении через них быстрых электронов помимо имеющей место флуоресценции испускают слабое световое излучение, имеющее непрерывный частотный спектр. Излучение направленно вперёд максимумом вдоль образующей конической поверхности с углом 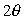 , определяемым выражением (4.29b), ось которой совпадает с направлением движения электрона. Свечение частично поляризовано так, что плоскость колебаний вектора напряжённости электрического поля преимущественно проходит через образующую указанного выше конуса и его осью. Излучение возникает практически мгновенно с началом движения и исчезает сразу же после прохождения электрона. Это позволило заключить Вавилову С.И. сделать вывод о том, что открытый вид излучения не является люминесценцией, для которой характерно конечное время свечения. К числу других свойств излучения относятся устойчивость излучения Вавилова и Черенкова к температурным воздействиям на среду, в которой движется электрон.
Теоретическое объяснение излучения Вавилова и Черенкова было сделано Таммом И.Е. (1895-1971) и Франком И.М. (р.1908). В 1934г. В 1940г. Л. Гинзбург (р.1916) создал квантовую теорию излучения Вавилова и Черенкова, основанную на законах сохранения энергии и импульса.
Явления, аналогичные излучению Вавилова и Черенкова, имеют место в аэродинамике и в гидродинамике. Примерами являются образование ударной волны Маха при движении самолётов со скоростью, превышающей скорость звука, а также появление вспутной волны на поверхности воды при движении кораблей со скоростью, превышающей минимальную фазовую скорость, определяемую числом Рейнольдса.
Интересной является интерференционная интерпретация с помощью излучения Вавилова и Черенкова закона Снеллиуса, определяющего углы отражения и преломления электромагнитной волны при прохождении ей границы раздела двух диэлектриков (магнетиков) с различными значениями показателей преломления.
Для простоты предположим, что на поверхность диэлектрика с показателем преломления 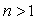 под некоторым углом 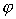 (рис. 4.31) падает гармоническая электромагнитная волна, поляризованная параллельно поверхности диэлектрика. Тогда образование отражённой от границы и прошедшей границу вакуум / диэлектрик электромагнитных волн является следствием излучения диполей, образующихся на границе под действием падающей электромагнитной волны, излучение которых является когерентным. Представим, что диполи образуются возмущением электромагнитного поля, вызываемого действием падающей электромагнитной волны на электронные оболочки атомов и молекул диэлектрика и распространяющегося вдоль границы раздела двух сред со скоростью (рис. 4.30) равной
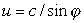 . . | (4.30) |
Движение возмущения электромагнитного поля по своим последствиям эквивалентно движению заряда со скоростью 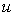 , способного при условии превышения скорости движения заряда фазовой скорости света 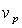 в среде вызвать излучение Вавилова и Черенкова . Направление излучения Вавилова и Черенкова в соответствии с (4.29b) и (4.30) составляет угол 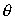 с направлением движения, определяемый из выражения:
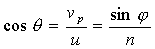 .
Замечая, что 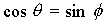 , получаем закон Снеллиуса:
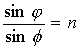 . . | (4.31a) |
Аналогично рассуждая, получаем, что отражённая от поверхности диэлектрика электромагнитная волна в вакуум также может быть интерпретирована как излучение Вавилова и Черенкова из- за перемещения возмущения электромагнитного поля со скоростью (4.30), максимум которого в вакууме ( 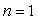 ) составляет угол 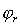 с направлением движения, определяемый из выражения (4.29b):
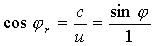 .
Замечая, что 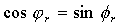 , получаем закон Снеллиуса, определяющего закон зеркального отражёния электромагнитной волны от поверхности диэлектрика:
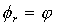 . . | (4.31b) |
Таким образом, отражение и преломление света от границы раздела двух сред можно рассматривать, как одно из проявлений излучения Вавилова - Черенкова.
|