3.2 Классификация сред распространения электромагнитных волн
Наиболее простой средой с точки зрения эффектов, сопровождающих распространение электромагнитных волн, является вакуум. Вакуум представляет собой единственную среду распространения электромагнитных волн, в которой нет дисперсии и потерь, а скорость распространения электромагнитных волн не зависит от частоты. Волновое число 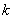 определяет пространственную периодичность (длину волны 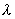 ) электромагнитной волны частоты 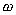 в направлении своего распространения:
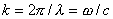 . . | (3.16a) |
Отметим, что из этой формулы следует фундаментальный вывод о связи пространственной 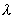 и временной периодичности (периода 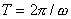 ) волны, определяемой своей частотой. Фундаментальность этого вывода связана тем, что это является лишь частным случаем проявления взаимосвязи временных и пространственных характеристик электромагнитных волн более сложной структуры, чем плоские, в чем мы убедимся ниже в главе 5 при изучении явления когерентности электромагнитных волн.
На практике вакуум может являться достаточно адекватной моделью распространения электромагнитных волн в сухом воздухе и в разреженных газообразных средах.
В диэлектриках, не являющихся проводниками электричества, при постоянных электрических и магнитных полях проводимостью можно пренебречь. При малых частотах электромагнитного поля значение диэлектрической и магнитной проницаемости можно считать не зависящими от частоты и равными статическим значениям, имеющим место для постоянных полей. В этом случае пространственная и временная периодичности электромагнитной волны имеют качественно такой же характер связи, как и в вакууме. Количественное отличие касается зависимости величины фазовой скорости распространения волны от оптической плотности среды 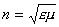 , в результате которой длина волны 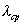 электромагнитной волны в среде оказывается в 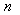 раз меньше волны  в вакууме:
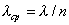 | (3.16b) |
Это свойство электромагнитной волны при распространении на некоторое расстояние 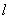 в среде с оптической плотностью 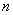 позволяет определить оптическую длину пути 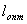 , проходимого волной в среде, определяемую следующим выражением:
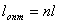 . . | (3.16c) |
Понятие оптической длины пути и связанное с ним понятие оптической разности хода волн лучей широко используется для объяснения многих оптических явлений и понимания принципов работы оптических приборов.
При распространении электромагнитной волны в среде изменяется по сравнению с вакуумом также соотношение между амплитудами её векторов напряженностей электрического и магнитного полей ввиду зависимости величины волнового сопротивления среды от отношения электрической и магнитной проницаемостей, даваемой формулой (3.3).
При увеличении частоты необходимо учитывать зависимость комплексных значений электрической и магнитной проницаемостей среды от частоты, вследствие особенностей физических процессов поляризации или/и намагничивания среды при распространении электромагнитной волны в диэлектрике / магнетике.
Для примера можно указать статическое значение относительной диэлектрической проницаемости воды для постоянных полей 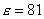 . Для волн инфракрасного диапазона, соответствующих длине волны 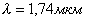 , значение комплексной диэлектрической проницаемости 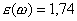 . Объяснение особенностей зависимости 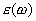 воды от частоты исходит из представлений о воде, как о полярном диэлектрике, поляризация которого происходит вследствие поворота имеющих большую инерцию молекул воды под действием переменного электрического поля электромагнитной волны. Особенно сильная дисперсия резонансного характера отмечается для частот сантиметрового диапазона электромагнитных волн (длина волны 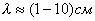 ).
Сильную дисперсию имеет водяной пар в диапазоне миллиметровых волн ( 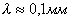 ) .
Как правило, сильная дисперсия в некотором диапазоне частот сопровождается значительными потерями энергии распространяющихся электромагнитных волн из-за резонансного характера взаимодействия электромагнитной волны с атомами и молекулами среды.
Для неполярных диэлектриков, как то - воздух, бензол, водород, гелий, неон и др. инертные газы, сера , алмаз, соотношение
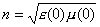 , , | (3.17) |
определяемое статическими значениями относительных диэлектрических и магнитных проницаемостей, остаётся справедливым вплоть до оптического диапазона электромагнитных волн ( частота 10 14 ... 10 15 герц ).
Объяснение этого факта основано на том, что в неполярных диэлектриках поляризация происходит за счёт деформации электронной оболочки составляющих их атомов и молекул. Ввиду малой инерционности электронов вектора смещения и напряженности электрического поля колеблются практически в одной фазе вплоть до весьма высоких частот электромагнитных волн, что и приводит к малой дисперсии неполярных диэлектриков.
Можно показать, что резонансный характер взаимодействия электромагнитных волн с электронами атомов и молекул неполярных диэлектриков приводит к следующей характерной зависимости их комплексной диэлектрической проницаемости 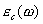 от частоты:
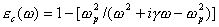 ,
где 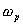 - резонансная частота; 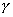 - коэффициент, учитывающий потери электромагнитной волны на поляризацию диэлектриков.
В реальных диэлектриках, как правило, комплексная диэлектрическая проницаемость может иметь несколько резонансных частот 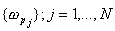 , которым будет соответствовать сумма в выражении для 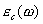 :
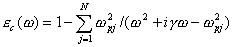 .
Следующий рассматриваемый класс сред распространения составляют металлы, являющиеся проводниками электричества.
Для неферромагнитных материалов их электродинамические свойства определяются исключительно проводимостью вещества. Как показывает опыт, проводимость металлов во всем диапазоне электромагнитных волн радиочастотного диапазона вплоть до миллиметровых волн сохраняет своё значение, имеющее место для статических полей (при постоянном токе). В оптическом диапазоне, начиная с инфракрасного диапазона, электродинамические свойства имеют более сложный характер в зависимости от частоты электромагнитных волн.
Характерной особенностью комплексной диэлектрической проницаемости 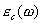 металлов металлов является значительное превосходство по величине мнимой части 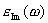 над действительной 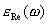 , которой по этой причине обычно пренебрегают, т.е. полагают в соответствии с формулой (3.14), что:
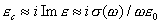 . . | (3.18) |
Величина проводимости для хороших и плохих проводников могут отличаться на два порядка. В качестве примера рассмотрим медь с величиной удельной проводимости  ом -1метр -1, относящуюся к хорошим проводникам , и висмут, являющийся полуметаллом 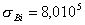 ом -1метр -1.
Найдем значения модулей мнимых частей комплексной диэлектрической проницаемостей для рассмотренной пары металлов по формуле (3.18) для световых волн (частота 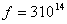 гц):
Отсюда следует, что для всех металлов во всем диапазоне радиочастот и отчасти в оптическом диапазоне  . Это оправдывает пренебрежение действительной части по сравнению с мнимой при расчёте комплексной диэлектрической проницаемости по формуле (3.18).
Из других проводников отметим электролиты, проводимость которых обусловлена ионами. Проводимость электролитов при низких частотах электромагнитных волн весьма высокая. Однако с ростом частоты проводимость падает и для большинство электролитов для оптического диапазона прозрачны. Отметим, что факт прозрачности вещества говорит об отсутствия поглощения электромагнитных волн из-за наличия мнимой части комплексной диэлектрической проницаемости, обусловленной в основном проводимостью. Для поваренной соли проводимость снижается уже в метровом диапазоне электромагнитных волн.
Отметим, что в зависимости от диапазона электромагнитных волн не только проводники могут становиться изоляторами, как в примере с поваренной солью, но и наоборот - изоляторы могут становиться проводниками, как это имеет место для этилового спирта, который начинает эффективно поглощать электромагнитные волны в диапазоне длин волн 3 см - 20 см.
Магнитные свойства ферромагнитных веществ весьма сильно изменяются с частотой. Так для ферромагнитных сердечников используемых в радиотехнике значение магнитной проницаемости резко уменьшается с ростом частоты, начиная со звуковых частот (10 - 20 Кгц ) электромагнитных волн.
Специальные магнитные материалы - ферриты , приготовленные на основе порошковой технологии из ферромагнетиков , сохраняют большие значения магнитной проницаемости, характерные для обычных ферромагнетиков для статических полей, и для радиочастот, вплоть до сверхвысокочастотного диапазона электромагнитных волн.
Интересными электродинамическими особенностями обладает плазма. Для не слишком интенсивных электромагнитных полей в первом приближении плазму можно считать средой с магнитной проницаемостью 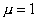 и диэлектрической проницаемостью 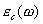 , которая может быть вычисляемой по формуле:
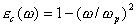 , , | (3.19) |
где 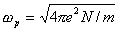 - т.н. плазменная частота, 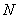 - концентрация свободных электронов.
Из формулы (3.19) следует, что электромагнитные волны в плазме, частота которых меньше плазменной частоты не распространяются, поскольку диэлектрическая проницаемость плазмы для таких частот отрицательна и, следовательно, показатель преломления и волновое число чисто мнимое.
Понятие комплексной диэлектрической проницаемости среды позволяет рассмотреть с единых позиций комплексных уравнений Максвелла распространение электромагнитных волн в различных средах, что заслуженно имеет большое научно-практическое значение для решения широкого круга естественно - научных и технических задач.
|