2.2 Определение электромагнитных полей колеблющегося заряда
С помощью выражения (2.7) найдем индукцию магнитного поля, принимая во внимание, что вектор 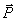 имеет отличную от нуля 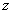 составляющую, а остальные его компоненты равны нулю. Следовательно, вектор индукции 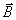 расположен в плоскости перпендикулярной оси 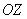 (рис.2.3).
Выполняя дифференцирование в (2.7), получим выражение для 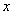 - ой компоненты вектора индукции магнитного поля:
 , , | (2.8a) |
где при выводе использовались следующие очевидные формулы дифференцирования 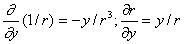 ; а также введено обозначение для второй производной от вектора дипольного момента по времени:
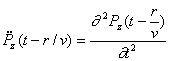 .
Аналогичным образом может быть рассчитана 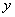 - ая компонента вектора индукции магнитного поля:
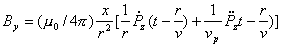 , , | (2.8b) |
С помощью (2.8) можно написать векторное равенство:
 . . | (2.9a) |
Отметим очевидный факт, что если бы не зависимость аргумента первого слагаемого в этом выражении от 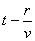 , то оно точно определяло бы магнитное поле 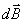 , возбуждаемое, протекающим в 'малом ' объёме 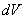 стационарным током с плотностью 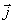 и рассчитываемое исходя из закона Био - Савара -Лапласа:
 , , | (2.9b) |
где 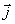 - плотность тока, эквивалентного движению заряда вдоль оси 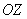 и в соответствии с (2.6) равного:
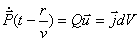 .
Таким образом, выражение (2.9a), определяющее магнитное поле движущегося заряда, отличается от (2.9b), следующего из закона Био - Савара - Лапласа для расчёта магнитного поля стационарного тока. Во-первых, в (2.9a) имеется дополнительное (второе) слагаемое, отсутствующее в (2.9b). Во-вторых, магнитное поле, определяемое (2.9a), имеет волновой характер, поскольку учитывает конечную скорость волны при её движении от заряда до точки наблюдения.
Рассмотрим роль второго слагаемого в (2.9a) для расчёта магнитного поля движущегося заряда. Очевидно, на малых расстояниях 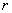 от движущегося заряда ( 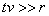 ) можно пренебречь волновым характером его магнитного поля (влиянием запаздывания) и его можно рассчитывать исходя из закона Био - Савара - Лапласа (2.9b). Действительно, можно показать, что вблизи движущегося заряда второе слагаемое в (2.9a) стремится компенсировать эффект запаздывания первого слагаемого. В этом нетрудно убедиться, разлагая для малых значений 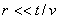 в ряд Тейлора функцию 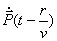
и, принимая во внимание, что в том же порядке малости справедливо равенство 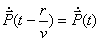 , из (2.9a) получается (2.9b).
Рассмотрим магнитное поле движущегося заряда на большом расстоянии от него 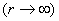 . Тогда из формулы (2.9a) следует, что индукция магнитного поля определяется вторым слагаемым, превышающим по порядку величины первое слагаемое, которым можно пренебречь. В результате индукция магнитного поля движущегося заряда при 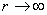 может быть рассчитана по формуле, которая с учётом очевидного обобщения на случай излучения электромагнитных волн в среде с диэлектрической 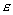 и магнитной 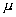 проницаемостью, может быть записана следующим образом:
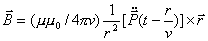 | (2.10a) |
Учитывая связь вектора напряженности магнитного поля 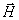 и вектора индукции магнитного поля 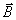 в вакууме, отсюда следует, что:
 . . | (2.10b) |
Из полученных выражений следует, что магнитное поле электромагнитной волны движущегося заряда убывает на значительном расстоянии от него обратно пропорционально расстоянию. Следовательно, электромагнитная волна, возникающая при движении заряда, в соответствии со сказанным в гл.2 является сферической (рис.2.4) 1, излучаемой из точки расположения заряда ввиду малости размеров занимаемого им объёма. Это обстоятельство облегчает нахождение вектора напряженности 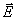 электрического поля электромагнитной волны движущегося заряда .
В самом деле, на значительном расстоянии от центра излучения заряда сферическая волна локально в окрестности произвольной точки наблюдения может быть представлена как плоская волна (рис.2.5), распространяющаяся в направлении луча от центра к точке наблюдения. В плоской волне вектора напряженности электрического 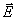 , магнитного полей 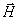 и направление распространения волны образуют правую тройку векторов, что позволяет однозначно определить направление и величину вектора 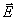 по известному вектору 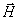 с помощью соотношения (1.12a). Следовательно, напряжённость электрического поля в электромагнитной волне, излучаемой движущимся зарядом в среде с диэлектрической 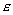 и магнитной 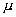 проницаемостью, определяется формулой:
 , , | (2.11a) |
где при преобразованиях были использованы формулы для волнового сопротивления вакуума (1.13) и скорости света (1.7) , выражающие эти величины через электрическую 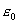 и магнитную 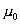 постоянные.
Учитывая связь (1.1a) между вектором напряженности электрического поля и вектором смещения электрического поля 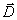 , получаем:
 , , | (2.11b) |
где 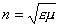 - показатель преломления среды, определяемый (1.14).
Из выражений (2.10) и (2.11) следуют четыре важные свойства электромагнитного излучения движущегося заряда, справедливые и при более общих предположениях, чем были сделаны выше при их выводе.
Во-первых, электромагнитная волна, излучаемая движущимся зарядом, возникает только при условии неравномерного движения электрического заряда, поскольку в противном случае 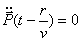 .
Во вторых амплитуды векторов электрического и магнитного полей электромагнитной волны, излучаемой движущимся зарядом, убывают обратно пропорционально расстоянию по мере удаления точки наблюдения от заряда, как и должно быть в сферической волне, излучаемой точечным зарядом.
В-третьих, электромагнитная волна имеет определённую пространственную ориентацию векторов напряженности электрического и магнитных полей по отношению к направлению движения заряда. Иными словами, электромагнитная волна, излучаемая движущимся зарядом, поляризована.
Рассмотрим поляризацию сферической электромагнитной волны, излучаемой движущимся зарядом, более подробно. Для этого вообразим сферу (рис.2.5), описанную вокруг заряда как из центра. В любой точке сферы в соответствии с выражениями (2.10) и (2.11) вектора 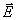 и 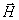 электромагнитной волны располагаются в плоскости, касательной к поверхности сферы в точке наблюдения.
Вектор напряженности магнитного поля 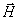 направлен по касательной к окружности, представляющей собой сечение сферы плоскостью, проведенной через точку наблюдения перпендикулярно оси 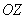 , вдоль которой движется заряд. Направление вектора 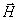 совпадает с направлением обхода указанной выше окружности против часовой стрелки, если смотреть на нее со стороны положительного направления оси 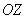 в соответствии с правилом вычисления направления вектора результата векторного произведения (2.10).
Вектор напряженности электрического поля 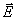 направлен по касательной к окружности, представляющей собой меридиональное сечение сферической поверхности, т.е. сечение сферы плоскостью, проходящей через ось 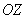 и точку наблюдения. Направление вектора 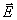 совпадает с направлением обхода указанной окружности по часовой стрелки.
Наиболее наглядно можно представить направление векторов напряжённостей электрического и магнитного полей в сферической системе координат 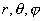 с центром в начале декартовой системы координат 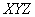 (рис.2.6):
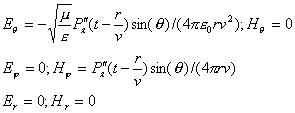 | (2.12) |
Четвёртое свойство электромагнитного излучения движущегося заряда заключается в том, вдоль направления его движения электромагнитное излучение отсутствует. В самом деле, из (2.12) следует, что по мере приближения точки наблюдения на поверхности сферы к её полярным областям , т.е. к тем местам сферической поверхности, где она пересекается с осью 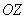 , что имеет место при 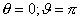 , амплитуда векторов электрических и магнитных полей сферической волны стремится к нулю и обращается в нуль в точках пересечения поверхности сферы с осью 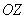 (рис.2.6) .
Если обратить внимание на то, что все электрические и магнитные поля в формулах (2.10) и (2.11) определяются дипольным моментом колеблющегося заряда, то становится понятным, почему его электромагнитное излучение называется дипольным.
Дипольное электромагнитное излучение может быть реализовано на практике с помощью диполя Герца, представляющего собой элементарный электрический излучатель электромагнитных волн c длиной волны 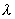 , возникающих в результате протекания переменного тока частотой 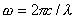 по проводнику длиной 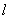 .
Если предположить, что ток в проводнике изменяется во времени по гармоническому закону 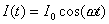 , то ему будет соответствовать изменяющийся во времени дипольный момент 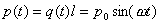 , где 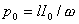 . Как видим, колебательному движению заряда в проводнике соответствует гармоническое изменение во времени дипольного момента заряда. Тогда, отлична от нуля вторая производная дипольного момента в (2.12):
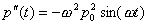 .
Используя это соотношение (2.12), выпишем в сферической системе координат компоненты векторов напряжённости электрического и магнитного полей электромагнитной волны, излучаемой диполем Герца:
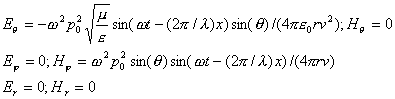 | (2.13) |
Экспериментальные исследование излучения и приёма электромагнитных волн, проведенные Г. Герцем.
Открытие, а также теоретическое и экспериментальное исследование свойств электромагнитных волн было сделано Г. Герцем (1887-1888). В качестве источника электромагнитных волн Г. Герц использовал изобретённый им излучатель (рис.2.7), впоследствии названный в его честь диполем Герца.
Как следует из рисунка диполь Герца представляет собой два соосных проводника (полых внутри), разделённых небольшим промежутком , который называется искровым. Два ближайших конца проводников подключены к выходным клеммам источника электрического напряжения ( индуктора), величина которого может плавно изменяться. При достаточно большом значении напряжения генератора возникает электрический пробой промежутка между вибраторами, в результате которого проскакивала искра в искровом промежутке. Катушки индуктивности 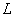 предназначены для предотвращения попадания колебаний тока на вибраторе обратно в индуктор.
Как следствие этого в двух проводниках диполя Герца возникают собственные затухающие колебания электрического тока, имеющие узлы на концах проводников. Из всех возможных типов колебаний тока (мод) наибольшую амплитуду имеют колебания с пучностью тока посредине диполя. Длина волны 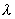 такого колебания примерно равна удвоенной длине диполя 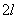 .
Итак, колебания электрического тока в вибраторах диполей Герца вызываются искрой, представляющей собой достаточно быстро меняющийся во времени электрический ток, который в соответствии с системой уравнений Максвелла (1.1b) и является источником электромагнитной волны.
В опытах Герца электромагнитная волна обнаруживалась с помощью т.н. резонаторов, которые в современном представлении являются ничем иным, как антеннами. Так, Г. Герц использовал изобретённый им резонатор (рис.2.8) в виде точной копии по размерам диполя, используемого для излучения электромагнитной волны, который предстоит обнаружить. О наличии колебаний токов в вибраторах резонатора можно было судить о проскакивании электрической искры или свечении газоразрядной трубки GT (рис.2.8), подключаемой к искровому промежутку резонатора.
Для исследования свойств электромагнитных волн, изучению которых мы посвящаем следующие главы, необходимы более мощные и стабильные во времени источники электрического напряжения, чем рассмотренный выше индуктор. В качестве таковых в настоящее время используются генераторы гармонических колебаний, частота 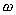 которых выбирается соответстующей длине волны 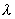 , равной удвоенной длине диполей 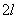 для резонансного увеличения амплитуды токов в приёмном и передающем диполях . Для опытов Герца использовались колебания, частота которых 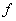 составляла примерно 5 10 8.колебаний в секунду, что соответствует длине волны 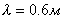 при длине вибраторов 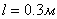 .
Для определения наличия или отсутствия электромагнитных волн вокруг передающего вибратора вместо газоразрядной трубки, включаемой между плечами приёмного вибратора, использовался прибор, называемый когерер , с последовательно подсоединённым к нему амперметру в соответствии с рис.2.9a . Когерер представляет собой запаянную стеклянную трубку внутри которой находятся оксидированные металлические опилки .
В обычных условиях сопротивление опилок по постоянному току очень велико. По этой причине при отсутствии в месте нахождения приёмного вибратора электромагнитной волны амперметр в цепи когерера имеет нулевые показания. При приёме электромагнитной волны между плечами приёмного вибратора проскакивает искра, вызывающая внутри когерера "спекание" металлических опилок. В результате сопротивление когерера резко уменьшается и амперметр отмечает отклонением стрелки протекание электрического тока. По величине тока, пропорционального значению напряжённости электрического поля принимаемой волны, можно сделать вывод об интенсивности электромагнитной волны, излучаемой передающим вибратором на разных расстояниях от него и при разных ориентациях плеч приёмного и передающего вибраторов. Отметим свойство когерера восстанавливать состояние своего большого сопротивления после окончания протекания электрического тока в результате лёгкого "потряхивания" стеклянной трубки.
В современных демонстрациях опытов Г. Герца вместо когерера или газоразрядной трубки может быть использован полупроводниковый диод. Благодаря свойству односторонней проводимости диода электромагнитная волна принимается только в моменты времени, соответствующие положительным значениям напряжённости электрического поля волны. По этой причине амперметр, включённый в цепь с диодом (рис.2.9b), отметит протекание постоянного тока, величина которого пропорциональна интенсивности электромагнитной волны.
Для упрощения изложения оригинальных опытов Г. Герца в дальнейшем при их описании будем предполагать, что между плечами приёмного вибратора включается электрическая лампа накаливания малой мощности. По величине или отсутствию накала этой лампы можно судить об интенсивности принимаемой электромагнитной волны.
В опытах Герца по исследованию законов излучения электромагнитных волн на некотором расстоянии от вибратора, излучающего волны, помещался приёмный вибратор, в промежуток между плечами которого присоединяется лампочка накаливания  малой мощности (рис.2.10).
При вращении приёмного вибратора вокруг своей оси в плоскости, параллельной плоскости расположения передающего излучения, наблюдается монотонное изменении накала лампы. Максимум накала имеет место при расположении приёмного вибратора параллельно передающему. Накал уменьшается до нуля, когда приёмный и передающего вибратора взаимно перпендикулярны. Это имеет место, вследствие излучения передающим вибратором линейно поляризованных электромагнитных волн, направление колебаний вектора напряжённости электрического поля которых параллельно плечам передающего вибратора. Таким образом, токи, возбуждаемые в приёмном вибраторе, оказываются пропорциональными косинусу угла между плечами приёмного и передающего вибратора. При перемещении приёмного вибратора параллельно передающему происходят затухающие колебания интенсивности накала по мере удаления приёмного вибратора от плоскости перпендикулярной плечам вибратора и проходящей через его середину. Колебания объясняются образованием в пространстве вокруг передающего вибратора суперпозиции волн, отражённых от окружающих передающий вибратор предметов (стен лаборатории, где проводится опыт, главным образом). В результате в пространстве, окружающем вибраторы, образуется подобие стоячей электромагнитной волны с чередующимися максимумами и минимумами, при прохождении которых меняется сила тока, возбуждаемого электромагнитным полем в приёмном вибраторе, пропорционально проекции вектора напряжённости электрического поля волны на направление плеч вибратора.
В ходе дальнейших исследований свойств электромагнитных волн Г. Герц обнаружил, что они полностью совпадают с известными в то время свойствами света. Более того, в ходе экспериментальных исследований было установлено, что законы распространения электромагнитных волн и света одинаковы. В частности, например, имеет место одинаковый характер отражения и преломления от диэлектрических и металлических тел, подробнее изучаемые в главе 4.
|