2.1 Волновой характер электромагнитного поля движущегося заряда
В предыдущей главе мы рассмотрели основные свойства электромагнитных волн, оставив в стороне "механизм" их возникновения. В этой главе мы обсудим проблему излучения электромагнитных волн, источниками которых, как мы установили выше, являются изменяющиеся во времени токи и/или неравномерно движущиеся электрические заряды.
Рассмотрим для определённости движущийся неравномерно электрический заряд. Неравномерное движение электрического заряда эквивалентно протеканию изменяющегося во времени электрического тока , меняющееся во времени магнитное поле которого , в свою очередь, создаст в окружающем пространстве электрическое поле и т.д. В результате этого процесса возникнет электромагнитная волна, источником которой является неравномерно движущийся заряд. Для определения электрического и магнитного поля возникающей волны необходимо решить систему уравнений Максвелла (1.1b), которая определяется распределением эквивалентного движению заряда тока. Необходимо отметить, что решение системы уравнений Максвелла для произвольно изменяющихся во времени и произвольно распределённых в пространстве токов и/или неравномерно движущихся зарядов представляет собой сложную математическую задачу. Однако при некоторых сделанных ниже разумных предположениях о характере движения заряда можно рассчитать его электромагнитное излучение и получить представление не только о механизме излучения электромагнитных волн, но и его основных свойствах.
В соответствии со сказанным выше рассмотрим задачу об излучении электромагнитной волны движущимся электрическим зарядом. Пусть заряд, распределённый в некотором, достаточно малом объёме 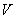 с плотностью 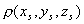 , движется в вакууме как целое со скоростью 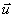 , зависящей от времени, вдоль оси 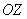 выбранной системы координат (рис.2.1). Это движение заряда будет эквивалентно протеканию электрического тока с плотностью 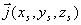 , равной:
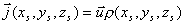 . . | (2.1) |
Как следует из уравнений Максвелла, в пространстве вокруг изменяющегося во времени тока возникнет электромагнитная волна. Рассчитаем электрическое и магнитное поле электромагнитной волны, излучаемой движущимся зарядом. Наиболее просто найти магнитное поле электромагнитной волны, создаваемое током, эквивалентным движению заряда. Электрическое же поле излучаемой волны, связанное с магнитным полем в силу уравнений Максвелла (1.1b), оказывается можно определить с помощью соотношений (1.12a), связывающих амплитуды векторов напряжённости электрического и магнитного полей в плоской гармонической электромагнитной волне.
Как известно, вектор индукции магнитного поля 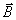 , создаваемый распределением тока с плотностью 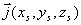 , может быть вычислен на основании закона Био - Савара - Лапласа с помощью принципа суперпозиции по формуле:
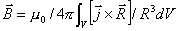 | (2.2) |
где 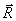 - радиус вектор, проведённый из точки интегрирования, принадлежащей объёму 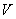 , в точку наблюдения  с координатами 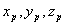 (рис. 2.1).
Для упрощения следующих далее расчётов магнитного поля выражение (2.2) может быть преобразовано с помощью правил дифференцирования сложных функций и свойств оператора пространственного дифференцирования 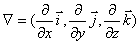 (см. задачу 2.1 в конце параграфа) следующим образом:
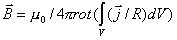 , , | (2.3) |
где 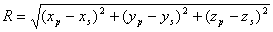 - расстояние между точкой объёма 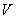 и точкой наблюдения 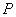 (рис.2.1).
В главе 1 мы отметили характерную особенность зависимости векторов напряжённости электрического и магнитного полей электромагнитных волн от координат и времени в виде следующих их комбинаций:
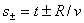 , , | (2.4) |
где 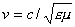 - фазовая скорость электромагнитной волны в среде с диэлектрической 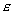 и магнитной 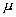 проницаемостями; 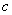 - скорость света в вакууме; 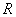 - расстояние, проходимое волной от источника до точки её наблюдения.
Напомним, что электромагнитная волна, вектора напряжённости электрического и магнитного полей которых зависят от комбинации 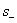 , распространяются от источника (объёма 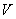 ) в окружающее пространство. Напротив, электромагнитная волна, вектора напряжённости электрического и магнитного полей которых зависят от комбинации, 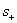 распространяется к источнику (объёму 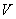 ) из окружающего пространства. При решении задачи об излучении волн из объёма 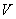 должен выполняться принцип причинности, в соответствии с которым электромагнитные волны, приходящие из окружающего объём 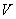 пространства должны быть исключены.
Следовательно, вектор индукции 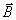 электромагнитной волны, возникающей при движении заряда в объёме электромагнитной волны, возникающей при движении заряда в объёме 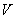 , может быть найден с помощью выражения:
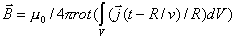 , , | (2.5) |
Из формулы (2.5) следует, что вектор индукции магнитного поля электромагнитной волны в точке наблюдения запаздывает по отношению к значениям этого вектора в точках объёма  . Это запаздывание является следствием распространения электромагнитной волны с конечной скоростью 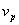 от точки источника в объёме  до точки наблюдения 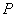 .
Решение задачи об излучении электромагнитных волн в ограниченную область пространства, окружающего объём 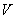 , или в пространство, включающего неоднородности в виде некоторых объектов , способных отражать электромагнитные волны, в том числе назад к их источникам, более сложно, поскольку в этом случае решение волнового уравнения представляется с помощью с помощью функций, зависящих как от  , так и от 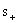 , определяемых выражением (2.4), и представляющих собой математическое выражение волн, распространяющихся навстречу друг другу в соответствии с решением волнового уравнения по методу Д'Аламбера .
Определим размер 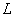 области пространства, занимаемой зарядом, величиной диаметра наименьшей сферы, внутри которой находится эта область. Предположим, что размеры 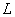 (рис.2.2) области пространства , занимаемой зарядом во много раз меньше расстояния 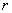 от ' центра ' заряда до точки наблюдения, т.е. 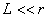 . Кроме того , будем полагать, что скорость движения заряда во много раз меньше скорости света, т.е. 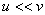 . В результате этих предположений выражение (2.5) упрощается:
Учитывая, что скорость всех точек объёма, занимаемого зарядом, одинакова, в результате очевидных упрощений получим следующее выражение для расчёта 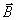 :
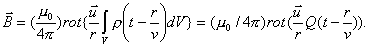 ,
где 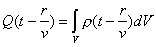 ) - полный заряд в движущемся объёме 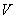 .
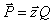 | (2.6) |
- дипольный момент объёмного заряда, имеющего малый размер,
С учетом этих упрощений получим:
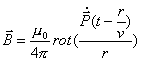 | (2.7) |
Показать, что вектор индукции магнитного поля 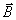 , создаваемого током с плотностью  в объёме 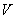 , может быть вычислен в точке наблюдения P с координатами  по формуле (2.3):
где  - расстояние между точкой объёма 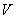 и точкой наблюдения 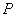 (рис.2.1).
Для преобразования исходной формулы (2.2) используем оператор  пространственного дифференцирования по координатам точки наблюдения 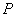 , определяемый формулой
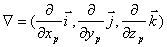 ,
где 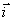 - единичный вектор в направлении оси 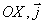 - единичный вектор в направлении оси 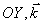 - единичный вектор в направлении оси 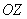 (рис.2.1).
Определим 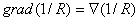 , используя правило дифференцирования сложной функции 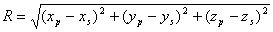 :
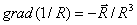 .
С помощью этого соотношения формула (2.2) будет иметь вид:
Замечая, что вектор плотности тока 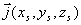 не зависит от координат точки наблюдения, можно преобразовать подынтегральное выражение, определяющее вектор 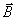 , с помощью дифференцирования произведения функций 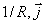 по переменным 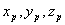 :
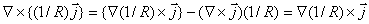 .
С учётом этого соотношения после цепочки очевидных преобразований получаем формулу (2.3):
|