1.1 Плоские электромагнитные волны
Понятие электромагнитной волны.
Как известно , электромагнитные поля определяются путём задания в каждой точке пространства четырёх векторов:
а) вектора напряжённости электрического поля 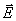 ;
б) вектора напряжённости магнитного поля 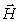 ;
в) вектора электрического смещения 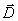 ;
г) вектора магнитной индукции 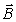 .
Эти векторы не являются независимыми. Попарно векторы  , а также 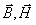 связаны друг с другом с помощью материальных уравнений. Наиболее простой вид материальные уравнения имеют для однородных изотропных сред, относительные значения диэлектрической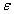 и магнитной 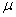 проницаемостей проницаемостей которых имеют постоянные значения для любой точки наблюдения электромагнитного поля:
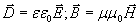 | (1.1a) |
Вектора  в общем случае зависят как от координат точки наблюдения 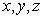 так и от времени 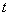 и могут быть найдены из системы уравнений Максвелла, решениями которой они являются:
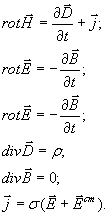 | (1.1b) |
В этих уравнениях: 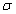 - коэффициент удельной электропроводности среды, в которой рассматривается электромагнитное поле, 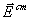 - напряженность электрического поля сторонних источников , 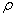 - объемная плотность сторонних электрических зарядов; 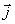 - плотность токов проводимости.
В дальнейшем будем называть сторонними токами, такие токи, которые вызываются электрическими полями  сторонних источников, причём, их плотность 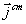 может быть вычислена по формуле: 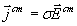 .
Отметим, что для полей независящих от времени 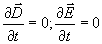 . В этом случае система (1.1b) распадается на две независимые системы: а) систему уравнений электростатики, определяющую постоянные во времени поля 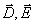 , и б) систему уравнений магнитостатики, определяющую постоянные во времени поля 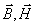 .
Для электромагнитных полей, зависящих от времени из системы уравнений Максвелла (1.1b) следует взаимосвязь изменения их электрических и магнитных полей . Наиболее просто в этом убедиться, если рассматривать зависящее от времени электромагнитное поле в среде, в которой нет сторонних зарядов, сторонних токов , плотность которых может быть вычислена по формуле 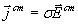 , и отсутствует проводимость ( 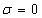 ) .
Таким условиям соответствует электромагнитное поле в вакууме, в котором отсутствуют источники сторонних токов и зарядов. Очень близкими свойствами обладает сухой воздух, проводимостью которого в обычных условиях можно пренебречь.
В этом случае первые два уравнения системы (1.1a) связывают между собой изменение в пространстве и времени электрического и магнитного полей. Отсюда следует основное свойство зависящих от времени электромагнитных полей, состоящее в согласованности изменения электрического и магнитного поля.
Так, при изменении во времени электрического поля возникает изменяющееся в пространстве переменное магнитное поле, которое приводит к появлению меняющегося в пространстве электрического поля. И, наоборот, при изменении во времени магнитного поля возникает изменяющееся в пространстве переменное электрическое поле, которое приводит к появлению меняющегося в пространстве магнитного поля.
Физическая причина такой взаимосвязи является следствием закона электромагнитной индукции и наличием тока смещения, связывающих между собой электрическое и магнитное поля. Причём, взаимосвязь электрических и магнитных полей имеет место даже в отсутствии сторонних токов и зарядов, являющихся источниками электромагнитного поля.
Процесс согласованного изменения электрического и магнитного полей в пространстве и времени, при распространении электромагнитного возмущения из одной точки пространства в другую, получил название электромагнитной волны.
Источниками электромагнитных волн, как это следует из системы уравнений Максвелла (1.1b), являются меняющиеся во времени сторонние токи и заряды. Исследование процесса излучения электромагнитных полей меняющимися во времени сторонними токами и зарядами будет более рассмотрено подробно в главе 2.
Существование электромагнитных волн впервые было предсказано английским физиком М.Ф. Фарадеем в 1832г. В 1865г. английский физик Дж. К. Максвелл теоретически показал, что скорость распространения электромагнитных волн в вакууме равна скорости света. Подтверждение открытых свойств электромагнитных волн и обширные их экспериментальные исследования было сделано немецким физиком Г. Герцем (1887-1888).
В ходе экспериментальных исследований свойств электромагнитных волн Г. Герц обнаружил, что законы распространения электромагнитных волн и света одинаковы. В частности, у них одинаковый характер преломления и отражения от диэлектрических и металлических тел. Часть из этих опытов мы изложим в дальнейшем по мере более детального изучения электромагнитных волн и оптики.
Виды электромагнитных волн.
Рассмотрим наиболее простой вид электромагнитных волн - электромагнитные гармонические (монохроматические) волны. Для электромагнитных гармонических волн величины векторов 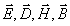 изменяются во времени по закону косинуса или синуса. Если какой либо один из четвёрки векторов электромагнитной волны меняется по закону косинуса или синуса, то, как это следует из системы уравнений Максвелла, и другие три вектора будут меняться во времени как функции синуса и косинуса.
Итак, изменение вектора напряжённости электрического поля 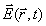 электромагнитной гармонической волны электромагнитной гармонической волны определяется следующим выражением:
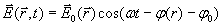 | (1.2) |
где  - радиус вектор точки наблюдения с координатами  - круговая частота колебаний [рад/сек], определённая периодом колебаний 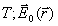 - амплитуда колебаний электрического поля, зависящая от положения точки наблюдения.
В дальнейшем будем называть полной фазой колебаний волны аргумент функции косинуса в выражении (1.2):
Значение начальной фазы 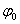 колебаний зависит от выбора момента начала отсчёта времени и/или положения центра декартовой системы координат. По этой причине можно считать  .
Из выражения (1.2) следует, что полная фаза гармонической волны имеет две составляющие:
а) временную составляющую фазы  , линейно изменяющуюся во времени со скоростью изменения, равной круговой частоте колебаний , линейно изменяющуюся во времени со скоростью изменения, равной круговой частоте колебаний  ; ;
б) пространственную составляющую фазы 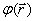 , характер зависимости которой от положения точки наблюдения 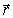 , как мы увидим ниже, определяется расстоянием  , пройденным волной от источника до точки наблюдения, т.е.:
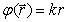 ,
- волновое число, определяемое длиной волны  - скорость света в вакууме).
Отсюда следует, что пространственная составляющая полной фазы является линейно изменяющейся функцией от расстояния, пройденного волной. Можно определить скорость изменения фазы волны в зависимости от пройденного волной расстояния величиной приращения фазы на расстоянии, равным единице длины ( в системе CИ - 1м). В соответствии с этим определением скорость изменения фазы волны в зависимости от пройденного волной расстояния равна волновому числу 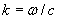 . По аналогии с круговой частотой  волновое число 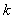 называют пространственной частотой. Размерностью волнового числа (пространственной частоты) в системе СИ является м -1 . В оптике используется внесистемная единица измерения волнового числа, имеющая размерность мм -1 и называемая 'числом линий на мм' . Физическое содержание такого названия станет понятным ниже в главе 5 при изучении явления интерференции света.
Особенностью гармонической электромагнитной волны (1.2) является зависимость полной фазы её колебаний 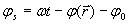 , как от времени, так и от положения точки наблюдения в пространстве.
Отметим, что периодичность изменения во времени гармонической, электромагнитной волны влечёт за собой в силу (1.1b) периодичность пространственного изменения векторов 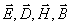 . В проявлении этого свойства гармонических электромагнитных мы убедимся далее.
Другим свойством электромагнитных волн является характер зависимости от положения точки наблюдения пространственной составляющей полной фазы и связанной с ней амплитуды колебаний четвёрки векторов электромагнитного поля.
В этом смысле самой простой гармонической электромагнитной волной является волна с постоянной амплитудой колебаний в любой точке наблюдения. Такие волны называются плоскими. Наиболее простое выражение для векторов электромагнитного поля имеет плоская гармоническая волна, распространяющаяся вдоль одной их координатных осей принятой декартовой системы координат 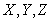 , например, вдоль оси 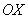 (рис.1.1). Колебания вектора напряжённости электрического поля такой волны будет определяться выражением
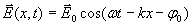 | (1.3a) |
где 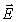 0 - амплитуда колебаний электрического вектора, постоянная во всех точках пространства; k x=(( 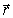 ) - пространственная составляющая полной фазы волны, которая имеющая постоянное значение в любой плоскости, параллельной плоскости ZOY, определяемое расстоянием, которое прошла волна от точки 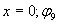 - начальная фаза колебаний волны при 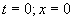 .
Колебания вектора напряжённости магнитного поля такой волны будет определяться аналогичным выражением
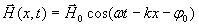 | (1.3b) |
где  - амплитуда колебаний электрического вектора, постоянная во всех точках пространства.
Кроме плоских гармонических волн известен достаточно широкий класс электромагнитных волн, у которых амплитуда изменяется с расстоянием. Наиболее простыми из них являются цилиндрические и сферические волны. Представление о цилиндрических волнах можно почерпнуть из наблюдений волн на поверхности воды в водоёме, после того, как в него брошен камень. Амплитуда и фаза колебаний четвёрки векторов цилиндрической волны имеет постоянное значение на концентрических поверхностях (рис.1.2a) вдоль оси симметрии которых расположены источники колебаний. На достаточно большом расстоянии 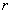 точки наблюдения от источника колебаний амплитуда, создаваемой им цилиндрической волны, убывает обратно пропорционально 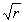 (см. задачу 1.1b).
Амплитуда и фаза колебаний четвёрки векторов сферической волны имеет постоянное значение на концентрических сферических поверхностях (рис.1.2b), в центре симметрии которых расположены источники колебаний. На достаточно большом расстоянии  точки наблюдения от источника колебаний амплитуда, создаваемой им сферической волны, убывает обратно пропорционально r (см. задачу 1.1a).
Поперечный характер электромагнитных волн.
В предыдущих параграфах мы рассмотрели основные свойства гармонических волн, вытекающих из очевидных и общих представлений о зависимости колебаний их векторов электрического и магнитного полей от времени и расстояния, пройденного волной от источника до точки наблюдения. Обоснуем эти соображения прямым решением системы уравнений Максвелла вместе с материальными уравнениями (1.1a) относительно четвёрки векторов 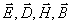 , определяющих электромагнитную волну.
Рассмотрим плоскую гармоническую электромагнитную волну круговой частоты  , распространяющуюся вдоль оси 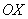 в однородной, непроводящей среде с ( 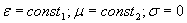 ).
Для такой волны в соответствии с её определением (1.3) вектора  не зависят от координат y и z, т.к. амплитуда их колебаний имеет постоянное значение для любой точки наблюдения, а фаза не изменяется в любой плоскости, параллельной плоскости 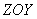 ( рис.1.1 ). Таким образом, вектора 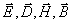 зависят только от времени 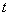 и координаты  . Исключая равные нулю частные производные компонент этих векторов по переменным  получим из (1.1b) определяющие каждую из декартовых компонент 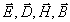 при  следующие уравнения:
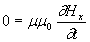 ; ; | (1.4a) |
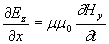 ; ; | (1.4b) |
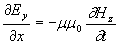 ; ; | (1.4c) |
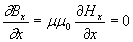 ; ; | (1.4d) |
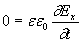 ; ; | (1.4e) |
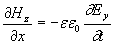 ; ; | (1.4f) |
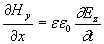 ; ; | (1.4g) |
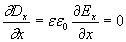 . . | (1.4h) |
Отсюда следует, что одним из решений системы (1.4) являются электростатическое и магнитостатическое поля, поскольку проекции на ось  любого из векторов электромагнитного поля 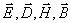 имеют равные нулю частные производные по координате  и времени 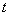 . Тогда , очевидно, 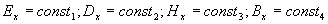 представляют постоянные электрическое и магнитное поля, ориентированные вдоль направления распространения плоской волны, накладывающиеся на меняющееся во времени электромагнитное поле волны и не зависящие от него. По этой причине без ограничения общности можно полагать их равными нулю, т.е.:
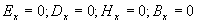 .
Следовательно, отличными от нуля компонентами плоской электромагнитной гармонической волны, распространяющейся вдоль оси  , являются:  , перпендикулярные 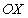 .
Отсюда следует важный вывод, что вектора напряжённости электрического и магнитного полей плоской электромагнитной гармонической волны колеблются в плоскости, перпендикулярной направлению распространения волны. Волны, обладающие таким свойством, называются поперечными. Следовательно, электромагнитные волны являются поперечными волнами (рис.1.3).
Поляризация колебаний плоской гармонической электромагнитной волны.
Второй важный вывод, который можно сделать из системы уравнений (1.4), состоит в том, что эта система уравнений представляет собой две независимые системы уравнений:
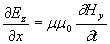 ; ; | (1.5a) |
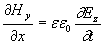 ; ; | (1.5b) |
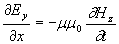 ; ; | (1.6a) |
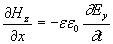 . . | (1.6b) |
Существование двух независимых друг от друга систем дифференциальных уравнений (1.5) и (1.6) позволяет рассматривать плоскую гармоническую волну с произвольной ориентацией вектора напряженности электрического поля электромагнитной волны в плоскости волнового фронта в виде суммы двух независимых плоских гармонических волн той же частоты, что и исходная, направления колебаний векторов напряженности электрического и магнитного полей взаимно перпендикулярны . Эта особенность векторного характера колебаний электромагнитной волны следует из законов электромагнетизма, составляющих физическую основу уравнений Максвелла. Действительно, пусть первоначально было переменное во времени электрическое поле  с направлением колебаний вектора напряженности электрического поля вдоль оси  , то возникнет ток смещения, благодаря которому генерируется магнитное поле 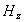 с колебаниями вдоль оси 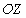 (рис.1.4a). Магнитное поле 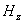 создаёт вихревое поле 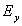 . При этом электромагнитное поле с компонентами 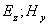 не возникает. Аналогично рассуждая, можно рассмотреть взаимное превращение первоначально созданного электрического поля 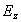 в магнитное поле 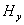 (рис.1.4b). При этом электромагнитная волна с электрическим и магнитным полями 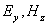 не возникает.
Возможность представления произвольной плоской гармонической электромагнитной волны в виде суммы двух независимых волн с перпендикулярно колеблющимися в одной фазе по отношению друг к другу парами векторов напряженности электрического и магнитного полей определяет свойство поляризации электромагнитной волны .
Поляризация электромагнитной волны определяется направлением колебаний вектора напряженности электрического поля . В рассматриваемом случае плоская волна, распространяющаяся вдоль оси  с произвольным направлением колебаний вектора напряженности электрического поля в плоскости  , может быть представлена в виде суммы двух электромагнитных волн , поляризованных в двух взаимно ортогональных направлениях, которые с учётом того, что ось  задаёт вертикальное направление по отношению к плоскости 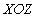 , отождествляемой с плоскостью горизонта, условно могут быть названы :
а) волны с горизонтальной поляризацией, определяемые колебаниями векторов 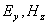 ;
б) волны с вертикальной поляризацией, определяемые колебаниями векторов  .
На рис.1.5 изображены направления колебаний соответствующие горизонтальной и вертикальной поляризации электромагнитных волн, распространяющихся со скоростью 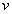 вдоль оси OX. Из этих рисунков следует, что вектора напряженности электрического 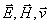 и магнитного  полей, а также скорости волны 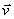 образуют правую тройку векторов. Направление колебаний векторов 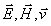 электромагнитной волны вертикальной поляризации, изображённой на рис.1.5a, получается после поворота тройки векторов рис.1.5a на 90 0 вокруг оси OX. Направление колебаний векторов 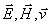 электромагнитной волны горизонтальной поляризации, изображённой на рис.1.5b, получается после поворота тройки векторов рис.1.5a на 180 0 вокруг оси OZ.
Волны с линейной поляризацией являются простейшими поляризованными волнами. Более сложным видом поляризации волн является круговая поляризация. В плоской электромагнитной волне круговой поляризации вектора напряженности электрического и магнитного поля равномерно вращаются вокруг своего направления распространения, образуя в каждый момент времени вместе с волновым вектором правую тройку векторов. Вращение указанных выше векторов может происходить как против часовой стрелки, так и по часовой стрелке, если смотреть с конца волнового вектора. Волны круговой поляризации волны с вращением векторов поля по часовой стрелке и против часовой стрелки являются волнами с ортогональными поляризациями. В соответствии с этим говорят о волнах, поляризованных по правому и левому кругу.
Очевидно, линейно поляризованная волна может быть представлена в виде суммы двух плоских волн с круговой поляризацией с равным значением модуля вектора напряженности электрического поля, в одной из которых вектор напряженности вращается по часовой стрелке, а в другой - против часовой стрелки (рис.1.6). Верно и обратное утверждение - волна круговой поляризации может быть представлена в виде суммы двух линейно поляризованных плоских волн с одинаковой амплитудой векторов напряженности электрического поля, фаза которых отличается на  , а направления колебаний в пространстве взаимно ортогональны.
Более общий вид поляризации электромагнитных волн представляет эллиптическая поляризация . Эллиптически поляризованная волна определяется как суперпозиция двух плоских электромагнитных неодинаковых по амплитуде волн линейной поляризации с взаимно ортогональным направлением колебаний в пространстве векторов напряжённости электрического поля каждой из волн, разность фаз колебаний которых отлична от  (рис.1.7) (см. задачу 1.2) . Конец вектора суммы этих электрических полей движется по эллипсу, что и объясняет название рассматриваемого вида поляризации. Параметрами эллиптической поляризации являются т.н. коэффициент эллиптичности поляризации волны, представляющий собой отношение полуосей эллипса, по которому в пространстве движется конец вектора суммарного колебания, и угол наклона оси эллипса, определяемый разностью начальных фаз составляющих колебаний.
Волновое уравнение. Связь амплитуд и фаз векторов напряженности электрического и магнитного полей плоской электромагнитной волны.
Ввиду независимости колебаний волн с ортогональными поляризациями дальнейший анализ свойств распространения плоской электромагнитной сосредоточим на изучении свойств волны одной какой-нибудь поляризации, например, горизонтальной с компонентами электрического и магнитного поля, соответственно равными 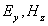 .
Убедимся, что компоненты электромагнитного поля 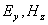 удовлетворяют волновому уравнению. Для этой цели продифференцируем уравнение (1.6a) по  , а уравнение (1.6b) по 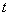 и после исключения смешанной производной получим:
 ;
Если подставить значения электрической и магнитной 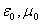 постоянных, то получим следующую величину их произведения:
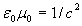 , , | (1.7) |
где 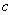 - скорость света в вакууме.
В силу соотношения (1.7) для определения E y получаем волновое уравнение:
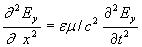 ; ; | (1.8a) |
Аналогично получается волновое уравнение для 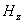 , а также для компонент плоской электромагнитной волны вертикальной поляризации 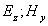 , определяемых (1.5) .
Уравнение (1.8a) называется волновым, в частности, из-за того, что его решением является плоская электромагнитная волна, определённая выше соотношением (1.3) для колебаний вектора напряжённости электрического поля:
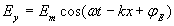 , , | (1.9a) |
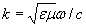 , , | (1.9b) |
- зависящее в общем случае от относительных диэлектрических и магнитных 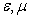 проницаемостей среды распространения электромагнитной волны.
Аналогичным образом можно убедиться, что решением волнового уравнения являются колебания вектора напряжённости магнитного поля 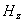 в виде плоской волны:
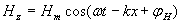 ; ; | (1.9c) |
В выражениях (1.9)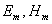 - амплитуды электрической и магнитной компонент плоской волны; 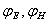 - начальные фазы колебаний векторов напряжённостей электрического и магнитного полей; 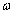 - частота волны.
Между амплитудами и фазами колебаний электрической и магнитной компонент электромагнитной волны имеются соотношения, следующие из системы уравнений (1.6) для горизонтальной поляризации 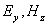 и системы уравнений (1.5) для волны вертикальной поляризации  . Подставим выражения (1.9) в (1.6):
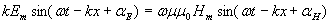 ; ; | (1.10a) |
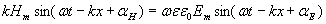 . . | (1.10b) |
Очевидно, для того, чтобы эти соотношения были справедливы для любых 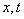 начальные фазы электрической и магнитной компоненты электромагнитной волны начальные фазы электрической и магнитной компоненты электромагнитной волны должны быть равными:
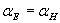 . . | (1.11a) |
Если это соотношение имеет место, то из (1.10) следуют два равенства, связывающие амплитуды электрической и магнитной компоненты 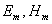 :
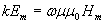 ;
 .
Перемножая эти равенства, получаем соотношение между амплитудами электрической и магнитной компонент плоской электромагнитной волны:
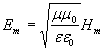 . . | (1.11b) |
Размерность коэффициента пропорциональности в соотношении (1.11b) между амплитудами электрической и магнитной компонент плоской волны, совпадает с размерностью ' сопротивления '. Действительно: размерность величины 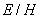 , обозначаемая символом - 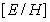 , равна: 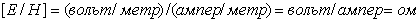 .
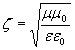 | (1.12) |
называется волновым сопротивлением среды распространения электромагнитных волн.
Для волны, распространяющейся в вакууме (в сухом воздухе)  :
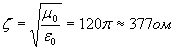 | (1.13) |
Величина 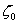 называется волновым сопротивлением вакуума.
Для вертикальной поляризации плоской волны с компонентами электрического и магнитного полей 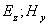 имеют место аналогичные соотношения (1.11), связывающие их амплитуды и фазы их колебаний .
Определим единичный вектор 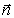 в направлении распространения волны, и одновременно перпендикулярный плоскости её волнового фронта.
Рассматривая (1.11) для двух возможных поляризаций плоской электромагнитной волны можно сделать вывод, что тройка векторов, состоящая из 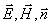 является правой. Это обозначает, что при наблюдении векторов  с конца вектора 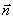 вектор 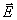 может быть совмещен с вектором 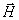 вращением против часовой стрелки в сторону меньшего угла.
С помощью вектора 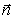 и выражений (1.12) могут быть получены соотношения для плоской гармонической электромагнитной волны, связывающее вектора  друг с другом с помощью векторного произведения (рис.1.3):
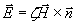 . . | (1.12a) |
Верным является и обратное соотношение:
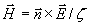 . . | (1.12b) |
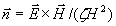 . . | (1.12c) |
На рис.1.8 изображена "мгновенная фотография" колебаний векторов напряжённости плоской электромагнитной волны, распространяющейся вдоль оси  .
В дальнейшем при изучении свойств электромагнитных волн с вектором 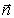 связывается волновой вектор 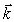
 ,
модуль которого определяется волновым числом (длиной волны), а направление совпадает с направлением распространения электромагнитной волны. В соответствии со сказанным выше тройка векторов, состоящая из 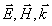 , является правой.
Фазовая и групповая скорости электромагнитной волны.
Электромагнитная волна, колебания векторов электрического и магнитного поля которой задаются уравнениями (1.9), представляет собой физический процесс, протекающий с конечной скоростью, равной скорости света 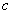 в среде, где она распространяется. Чтобы в этом убедиться рассмотрим волновое уравнение (1.8), в котором обозначим 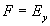 :
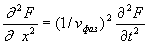 , , | (1.13a) |
где имеющий размерность скорости коэффициент
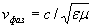 , , | (1.13b) |
определяет, как будет показано ниже, фазовую скорость распространения электромагнитной волны, зависящую от значений диэлектрической и магнитной проницаемостей среды её распространения.
Можно показать, что решением волнового уравнения (1.13a) является произвольная дважды дифференцируемая функция 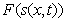 , например, изображённая на рис.1.9a, зависящая от линейной комбинации координаты и времени
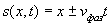 . . | (1.13c) |
Знак  в выражении (1.13c) означает, что решением уравнения (1.13a) является как функция 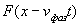 , так и функция  .
Функция 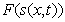 , изображённой на рис. 1.9a, при изменении времени перемещается вдоль оси 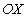 (рис.1.9b) в соответствии с нашими интуитивными представлениями о перемещении гребня волны. Это свойство решения уравнения (1.13b) явилось основанием назвать его волновым (Д' Аламбер).
Аргумент рассматриваемой функции  , называется, как и в частном случае плоской гармонической волны, полной фазой 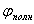 :
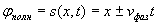 .
Множество точек в пространстве, в которых фаза волны имеет постоянное значение, называется волновым фронтом волны. Для рассматриваемого случая плоской волны (1.9) волновым фронтом является любая плоскость, параллельная плоскости 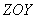 .
Физический смысл полной фазы состоит в том, что с её помощью можно определить перемещение волнового фронта волны из исходной точки 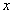 за время, равное 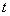 .
Решение волнового уравнения (1.13a) в виде плоской гармонической волны (1.9), очевидно, является частным случаем рассмотренного выше, когда в качестве произвольной функции 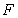 выбрана функция косинуса. Выражение для полной фазы плоской гармонической волны 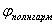 получается из выражения для полной фазы 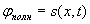 произвольной волны при умножении её величины, измеряемой в единицах длины (метрах), на волновое число  для пересчёта в радианы:
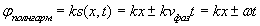 ,
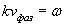 . . | (1.13d) |
Очевидно, полная фаза для рассматриваемой волны имеет постоянное значение  на любой плоскости, параллельной плоскости 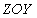 :
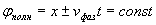 .
Это соотношение можно рассматривать, как уравнение для определения изменения положения выбранной плоскости постоянной фазы 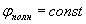 волны во времени :
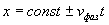 .
С помощью дифференцирования найдём скорость перемещения плоскости постоянной фазы, называемой фазовой скоростью  :
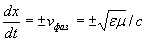 ,
Отсюда следует, что любая плоскость равной фазы для волны, представляемой функцией 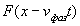 , перемещается со скоростью 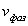 в положительном направлении оси 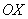 . Плоскость равной фазы для волны 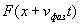 , перемещается со скоростью 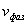 в отрицательном направлении оси 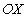 .
При рассмотрении свойств плоских электромагнитных волн мы ограничились случаем распространения волн вдоль оси  . Это не ограничивает строгость полученных результатов, поскольку с помощью поворота (вращения) осей используемой системы координат можно совместить направление распространения волны с одной из координатных осей, например, с осью 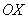 . Очевидно, величина перемещения плоскости равной фазы за время наблюдения не зависит от ориентации осей выбранной системы координат . Перемещение плоскости равной фазы волны отсчитывается вдоль перемещения волны, в направлении нормали к плоскости равной фазы, задаваемом единичным вектором 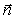 . Если учесть, что уравнение плоскости, нормаль которой задаётся вектором 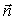 (рис.1.10), имеет вид 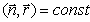 , где значение константы равно расстоянию от плоскости до начала координат, то величина перемещения волнового фронта, проходящего через начало координат при 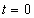 , за время наблюдения 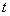 будет равно 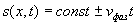 .
С учётом сказанного, выражение для плоской волны, распространяющейся в произвольном направлении, будет иметь вид  . В частности для плоской гармонической электромагнитной волны (1.9a):
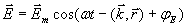 , , | (1.9d) |
где 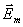 - вектор амплитуды колебаний напряжённости электрического поля волны, располагающийся в плоскости перпендикулярной направлению распространения волны.
Рассмотрим зависимость фазовой скорости электромагнитной волны от относительных значений диэлектрической и магнитной проницаемостей 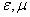 от параметров среды распространения. Из формулы (1.13c) следует, что в вакууме при 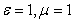 фазовая скорость распространения электромагнитной волны равна скорости света 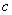 в вакууме. Это свойство электромагнитных волн является основанием одним из доказательств электромагнитной природы света.
В любой среде, где 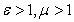 скорость распространения электромагнитной волны в  раз меньше, чем скорость света в вакууме.
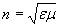 , , | (1.14) |
определяющая изменение скорости света в среде по сравнению c вакуумом, называется абсолютным показателем преломления среды или оптической плотностью среды.
Выражение (1.14) известно, как соотношение Максвелла, впервые установившего зависимость скорости электромагнитных волн от параметров среды их распространения.
Из-за уменьшения в 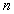 раз фазовой скорости электромагнитной волны в среде по сравнению со скоростью света в вакууме уменьшается её длина волны в среде в 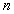 раз по сравнению со своим значением в вакууме. Действительно, за период колебаний волны 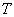 волна проходит с меньшей скоростью меньший путь:
 ,
где 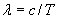 - длина волны в вакууме.
По этой причине электромагнитная волна, прошедшая некоторое расстояние 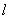 в среде с оптической плотностью 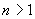 получит приращение своей фазы в  раз большее, чем при распространении в вакууме на тоже расстояние.
В заключении рассмотрим понятие групповой скорости электромагнитной волны. Необходимость рассмотрения наряду с фазовой скоростью также групповой скорости связана с негармоническими электромагнитными волнами. Оказывается, что электромагнитная волна с произвольной зависимостью от времени и координат точки наблюдения может быть представлена в виде суперпозиции плоских гармонических волн всевозможных частот.
В ряде случаев такая волна представляет собой некоторое ' возмущение ' электромагнитного поля, например, в виде импульса, равного нулю за пределами некоторого интервала 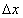 (объема  ) и промежутка времени 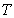 (рис.1.11a). Такое волновое поле называют волновым пакетом, если амплитуды гармонических волн, составляющих рассматриваемое возмущение, ' заметно ' отличаются от нуля лишь внутри некоторого интервала 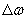 ' вблизи' средней частоты  0 (рис.1.11b). Если 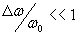 , то волна называется почти гармонической или квазигармонической. Волновые пакеты представляют большой практический интерес при рассмотрении взаимодействия электромагнитных волн с веществом, широко используются для передачи информации и пр. Поэтому имеет физический смысл оценка скорости движения волнового пакета или группы волн.
Такая скорость называется групповой и обозначается символом 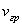 . Оказывается, перенос энергии электромагнитной волной осуществляется со скоростью, равной групповой.
Расчет групповой скорости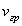 электромагнитной волны приводят к следующей формуле (см. задачу 1.3):
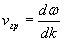 . . | (1.17a) |
Это выражение отличается от формулы для расчета фазовой скорости 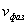 плоской гармонической волны частоты 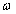 :
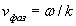 . . | (1.17b) |
Это различие имеет очевидную физическую причину, поскольку каждая из составляющих волновой пакет гармонических волн вследствие различия их частот (2.13d) имеет свою фазовую скорость.
Можно показать, что фазовая и групповая скорости связаны между собой соотношением:
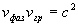 , , | (1.17c) |
где 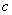 - скорость света в среде распространения электромагнитной волны.
Для плоских гармонических электромагнитных волн значения фазовой и групповой скоростей, рассчитываемых по формулам (1.17a) и (1.17b), совпадают.
а) амплитуда цилиндрической волны убывает обратно пропорционально корню квадратному из расстояния от центра её излучения.
б) амплитуда сферической волны убывает обратно пропорционально расстоянию от центра её излучения;
а) В самом деле, если бы амплитуда волны, излучаемой точечным источником, зависела от направления распространения, то среда распространения волны не могла бы считаться однородной и изотропной. Следовательно, амплитуда и фаза волны должны зависеть от расстояния от точки наблюдения до точки расположения источника. Далее, из изотропности среды распространения следует, что в единицу телесного угла точечный источник излучает одинаковую мощность не зависимо от ориентации рассматриваемого угла. Это обозначает, что через единичную площадку на поверхности волнового фронта волны, ориентированную перпендикулярно направлению распространения волны проходит мощность 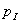 , излучаемая точечным источником, которая уменьшается обратно пропорционально квадрату расстояния от этой площадки до источника излучения. Действительно, через всю поверхность сферы радиуса r0 распространяется мощность  , равная мощности излучения источника. Следовательно, мощность 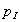 , проходящая через единицу поверхности сферы радиуса 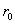 может быть определена из закона сохранения энергии :
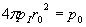 .
 .
Как будет показано в дальнейшем мощность излучения, проходящая через единичную площадку, ориентированную перпендикулярно направлению распространения волны представляет собой интенсивность излучения, пропорциональную квадрату амплитуды волны 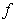 . Следовательно, амплитуда волны убывает обратно пропорционально расстоянию от точки излучения волны, т.е.:
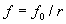 ,
где 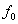 - коэффициент пропорциональности, определяемый мощностью источника волны.
Без потери общности можно считать, что источник помещается в начало координат, т.е. координаты точек источника 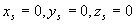 . Тогда расстояние r от точки расположения источника до точки наблюдения колебаний волны с координатами 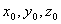 , равно:
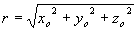 | (1.18a) |
Таким образом, амплитуда сферической волны имеет вид:
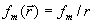 , , | (1.18b) |
где 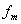 - амплитуда колебаний источника волны, а пространственная составляющая полной фазы сферической волны определяется выражением:
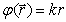 . . | (1.18c) |
Амплитуда и фаза сферической волны имеет постоянное значение на любой из сфер с центром в точке расположения источника (в нашем случае в начале координат), поскольку для 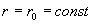 из (1.23a) следует, что
-уравнение сферы радиуса 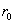 . Это свойство волны и послужило основанием для ее названия.
б) Повторим все рассуждения о соответствующих свойствах сферических волн, но с учетом цилиндрической симметрии амплитуды волн излучаемых источниками, расположенными на прямой. Цилиндрическая симметрия означает, что амплитуда волны одинакова на любой цилиндрической поверхности, ось которой совпадает с прямой расположения источников . Вследствие этого распределение амплитуд цилиндрической волны одинаково в любой плоскости перпендикулярной линии расположения источников. По этой причине при рассмотрении свойств цилиндрической волны будем рассматривать волну в одном из сечений, перпендикулярных линии расположения источников. Без ограничения общности линию расположения источников можно выбрать вдоль оси 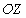 декартовой системы координат 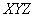 , а в качестве плоскости наблюдения волны плоскость 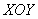 . Поскольку источник излучения в плоскости наблюдения 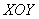 точечный, то на любой окружности с центром в начале координат мощность волны равна 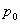 мощности излучения источника. Для интенсивности рассматриваемой цилиндрической волны 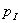 , представляющей собой мощность волны, проходящую через единицу длины окружности радиусом с центром в начале координат, из закона сохранения энергии получается уравнение 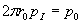 .
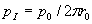 .
Поскольку амплитуда волны  пропорциональна корню квадратному из интенсивности волны, отсюда следует сформулированное выше утверждение:
 ,
где 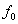 коэффициент пропорциональности, определяемый мощностью источника волны.
Пространственная составляющая полной фазы цилиндрической волны, очевидно, определяется выражением:
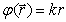 .
Плоская гармоническая электромагнитная волна, распространяющаяся вдоль оси 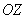 в вакууме, имеет в плоскости  следующие компоненты вектора напряжённости электрического поля: 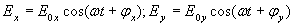 . Найти характер поляризации рассматриваемой электромагнитной волны.
Введём новые прямоугольные координаты 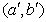 для обозначения компонент полей:
 .
Выразим из этих соотношений 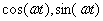 :
 ;
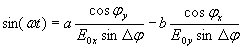 ,
где 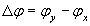 .
Возводя в квадрат каждое из равенств и складывая, получим в координатах 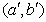 уравнение эллипса:
 .
Наиболее простой вид это выражение имеет после поворота системы координат 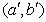 на угол  , определяемый из соотношения:
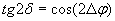 .
В повернутой системе координат 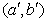 имеем каноническое уравнение эллипса:
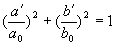 ,
где 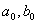 - полуоси эллипса, определяемые выражениями:
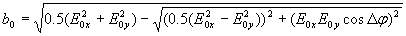 .
Отсюда следует, что поляризация рассматриваемой электромагнитной волны является эллиптической. Эллиптическая поляризация характеризуется т.н. коэффициентом эллиптичности 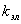 , по определению равным отношению полуосей эллипса:
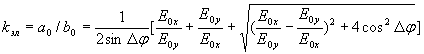 .
Ориентация осей эллипса определяется углом ( по отношению к оси OX, отсчитываемым против часовой стрелки , если смотреть с конца единичного вектора , ориентированного вдоль оси  .
Ответ: рассматриваемая в задаче электромагнитная волна имеет эллиптическую поляризацию с определённым выше коэффициентом эллиптичности.
Доказать, что групповая скорость 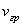 электромагнитной волны может быть вычислена по формуле:
Рассмотрим вывод формулы для расчета групповой скорости, исходя из определения скорости движения максимума волнового пакета.
Прежде всего, рассмотрим, как образуется максимум волнового пакета. Для конкретности предположим, что составляющие волновой пакет гармонические волны - плоские, распространяющиеся вдоль оси  . Тогда выражение для волнового пакета будет иметь вид:
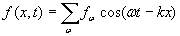 . . | (1.19) |
Для образования максимума все составляющие волновой пакет гармонические волны должны сложиться в фазе в точке максимума. Таким образом, максимум связан со стационарным значением фазы, что является прямым следствием принципа наименьшего действия, в оптике известного как принцип Ферма, согласно которому волна распространяется по траектории, длина которой (фаза) имеет наименьшее значение. Следовательно, в максимуме достигается минимум значения фазы волны (1.19), условием которого является следующее равенство:
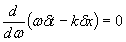 . . | (1.20) |
Пусть максимум волнового пакета имеет место при t=0 при x=0. Тогда при перемещении максимума за время 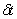 на 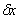 его положение можно определить из выражения (1.20) после соответствующего дифференцирования:
 .
Отсюда находим предел отношения 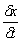 при 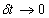 , являющийся искомым значением групповой скорости волнового пакета :
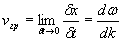 .
Рассчитаем групповую скорость плоской гармонической волны, исходя из (1.17a):
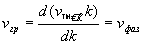 . . | (1.21) |
Таким образом, в однородной среде плоская гармоническая волна имеет одинаковые фазовую и групповую скорости, равные скорости света в среде, где эта волна распространяется. Легко показать, что сказанное выше справедливо также для сферических и для цилиндрических волн.
|